电路理论/最大功率传输

最大功率传输

我们通常希望尽可能多地将源的能量传输到其终端上的负载。我们如何确定负载的最佳电阻以实现这一点？

让我们考虑一个由戴维南等效电路建模的电源（诺顿等效电路将得出相同的结果，因为两者是直接等效的），并带有一个负载电阻R_L。源电阻为R_s，源的开路电压为v_s。

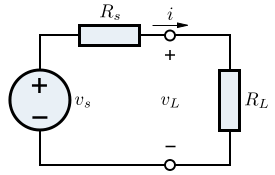
该电路中的电流可以使用欧姆定律计算

$i={\frac {v_{s}}{R_{s}+R_{L}}}$

负载电阻两端的电压v_L可以使用分压器规则计算

$v_{L}=v_{s}\,{\frac {R_{L}}{R_{s}+R_{L}}}$

现在我们可以找到负载中消耗的功率P_L，如下所示

$P_{L}=v_{L}i={\frac {R_{L}\,v_{s}^{2}}{\left(R_{s}+R_{L}\right)^{2}}}$

现在我们可以改写这个公式以消除顶部的R_L

$P_{L}={\frac {v_{s}^{2}}{\left({\frac {R_{s}}{\sqrt {R_{L}}}}+{\sqrt {R_{L}}}\right)^{2}}}={\frac {v_{s}^{2}}{R_{s}\left({\frac {\sqrt {R_{s}}}{\sqrt {R_{L}}}}+{\frac {\sqrt {R_{L}}}{\sqrt {R_{s}}}}\right)^{2}}}$

假设源电阻不可变，那么我们可以通过最小化上述公式分母中的括号部分来获得最大功率。这是一个基本数学结果，即$x+x^{-1}$ 当x=1时，达到最小值。在这种情况下，它等于 2。因此，上述公式在以下条件下达到最小值

${\frac {\sqrt {R_{s}}}{\sqrt {R_{L}}}}=1$

这导致了以下条件

$R_{L}=R_{s}\,$

如果负载电阻与源内部电阻相同，我们将从源中获得最大功率。这就是最大功率传输定理。

效率

效率η是指电路中所有消耗的能量中消耗在负载上的比例。我们可以立即看到，在最大功率传输到负载的情况下，效率为 0.5，因为源电阻两端的电压是其一半。我们还可以看到，效率会随着负载电阻的增加而增加，即使传输的功率会下降。

效率可以使用以下公式计算

$\eta ={\frac {P_{L}}{P_{L}+P_{s}}}$

其中P_s是源电阻中的功率。这可以通过对P_L公式进行简单的修改来找到

$P_{s}={\frac {v_{s}^{2}}{R_{L}\left({\frac {\sqrt {R_{s}}}{\sqrt {R_{L}}}}+{\frac {\sqrt {R_{L}}}{\sqrt {R_{s}}}}\right)^{2}}}$

下图展示了负载功率（占最大功率 *P_max* 的比例）和效率，负载电阻 *R_L* 的取值范围是源电阻 *R_s* 的 0 到 5 倍。

需要注意的是，在最大功率传输条件下，源端和负载端消耗的功率相等。如果电源是电力供应系统，负载是你的电加热器，这种情况并不理想。这意味着电力供应公司会浪费掉一半的电力。在这种情况下，发电机、输电线路等被设计成具有尽可能低的源电阻，以达到更高的效率。最大功率传输条件通常应用于（通常是高频）通信系统中，其中源电阻无法降低，功率水平相对较低，而且将尽可能多的信号功率传输到系统的接收端（负载）至关重要。