节点分析是在相量域中进行的。
节点分析方法减少了电路中需要求解的方程和未知量。
基尔霍夫方法找到所有电流和电压。节点分析只找到节点(连接点)的电压。
节点分析从基尔霍夫节点方程开始

并求解终端方程,使电流成为电压的函数,然后代入节点电流方程



什么是  ? 它是在所考虑器件两侧节点相对于地面的电压。
? 它是在所考虑器件两侧节点相对于地面的电压。

其中电流从 node_A 流向 node_B。
乍一看这可能看起来很琐碎,但在做问题时会暴露出一些细微的差异
- 节点电压是相对于地面的。它们不是基尔霍夫在单个器件上的压降。
- 假设所有电流都离开节点。
- 终端关系方程更复杂。
- 必须在相量域中进行,以便计算节点之间的阻抗。
- 可能方程太少,需要找到“超级节点”方程。
- 有些问题无法解决。识别这些并不容易。
 具有一个未知电压 V1 的基本示例电路。
具有一个未知电压 V1 的基本示例电路。
此电路中唯一的未知电压是 V1。有三个连接到该节点,因此需要考虑三个电流。计算中电流方向选择为远离节点。
- 通过电阻 R1 的电流: (V1 - VS) / R1
- 通过电阻 R2 的电流: V1 / R2
- 通过电流源 IS 的电流: -IS
根据基尔霍夫电流定律,我们得到

此方程可以关于 V1 求解

最后,可以通过用数字值替换符号来求解未知电压。在已知电路中所有电压后,任何未知电流很容易计算出来。

实际上, ,这意味着电流通过 R1 流动方向相反,这反映了这样一个事实:假设电流从节点流出只是为了帮助我们编写能够捕获电路拓扑的方程,以便写出逻辑一致的方程。它们决不是对最终电流方向的猜测。
,这意味着电流通过 R1 流动方向相反,这反映了这样一个事实:假设电流从节点流出只是为了帮助我们编写能够捕获电路拓扑的方程,以便写出逻辑一致的方程。它们决不是对最终电流方向的猜测。
给出下面的电路,找出所有节点的电压。
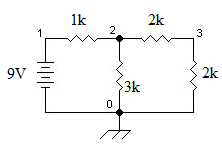 节点分析示例的电路示例。
节点分析示例的电路示例。
- 节点 0:
 (定义为接地节点)
(定义为接地节点)
- 节点 1:
 (自由节点电压)
(自由节点电压)
- 节点 2:

- 节点 3:

从而得出以下线性方程组

因此,解为

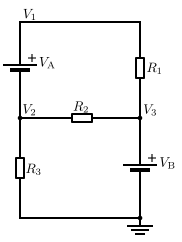 在这个电路中,VA 在两个未知电压之间,因此是一个超级节点。
在这个电路中,VA 在两个未知电压之间,因此是一个超级节点。
在这个电路中,我们最初有两个未知电压,V1 和 V2。由于电压源的另一端位于接地电位,因此 V3 上的电压已知为 VB。
流过电压源 VA 的电流无法直接计算。因此,我们无法编写 V1 或 V2 的电流方程。但是,我们知道离开节点 V2 的电流必须进入节点 V1。尽管节点无法单独求解,但我们知道这两个节点的组合电流为零。这种将两个节点组合在一起称为超级节点技术,它需要一个额外的方程:V1 = V2 + VA。
该电路的完整方程组为

将 V1 代入第一个方程,并针对 V2 求解,我们得到






















