所有电源可以是交流电 (AC) 或直流电 (DC)。
许多电源,例如电池或墙壁插座,都是电压源。这意味着它们会改变电流以保持电压恒定。AAA 和 AA 电池理想情况下始终输出 1.5 伏。大多数时候它们是断开的(未连接到任何东西)。最终它们会连接到一个从它们中汲取电流的电路。一个理想的 AAA 或 AA 电池可以提供无限的电流。一个现实世界的电池在短路时会试图提供无限的电流,但通常会发热、着火或爆炸 .
大多数消费者从未亲身体验过电流源。电路理论课程第一学期实验室部分的大多数学生也不会。电流源与电压源相反:它们通过改变电压来保持电流恒定。这使得它们非常危险。
电流源需要一根始终短路的电线。如果短路电线被移除,理想的电流源将立即产生最大、最可怕的闪电。
从概念上来说,电流源对于理解理想晶体管和运算放大器很重要。这就是为什么它们从一开始就是电路理论的一部分。在运算放大器和晶体管内部使用电流源几乎没有安全风险。
电源的电流和电压之间没有关系。一个 5 伏直流电源会根据连接的电路改变其电流。一个 5 安培直流电源会根据连接的电路改变其电压。
电源是一个依赖设备……依赖于以特定方式布置并连接到它的独立电阻器、电容器、电感器。
在任何给定时刻,流过一个双端器件的功率为: p ( t ) = v ( t ) i ( t ) {\displaystyle p(t)=v(t)i(t)}
时间 t 内消耗的平均功率为: p a v g ( t ) = 1 / t ∗ ∫ 0 t τ ∗ p ( τ ) d τ {\displaystyle p_{avg}(t)=1/t*\int \limits _{0}^{t}{\tau }*p({\tau })\,d{\tau }} s i n ( w t + θ ) {\displaystyle sin(wt+{\theta })} 2 π / w {\displaystyle 2{\pi }/w}
时间 t 内消耗的能量或完成的功类似: w ( t ) = ∫ 0 t p ( τ ) d τ {\displaystyle w(t)=\int \limits _{0}^{t}p({\tau })\,d{\tau }}
所有其他功率概念都源于以上。例如
如果电压和电流是恒定的(直流电),那么 p ( t ) = p a v g ( t ) = i v = i 2 R = v 2 / R {\displaystyle p(t)=p_{avg}(t)=iv=i^{2}R=v^{2}/R}
如果电压和电流是正弦的(交流电)并且已经过了足够的时间,使电路处于稳态,那么数学可以简化,但首先需要了解相量。但是,需要了解峰值功率、平均功率和功率因数概念,才能对电路形成直觉,并理解虚构的 "时间旅行器 "。
如果电压和电流呈任何模式并且处于稳态,那么上述数学可以简化。 电源有很多不同类型,每种类型都有不同的安全问题。如果过充,LiPo 电池会爆炸/着火 。这里有一个视频 ,一个男人探索 244 个失效的 9 伏电池,创造了一个 2000 伏电源。如果短路,电压电源也会发生这种情况。如果打开,电流源(非常罕见)也会发生这种情况。
在大多数实验室中,电源都由像家庭一样的保险丝保护。短路会导致断路器跳闸、保险丝烧断、继电器切断电路等。但电池通常没有保护。
大多数电源只是停止工作。
当电流 i ( t ) = 4 3 s i n ( 3 t ) {\displaystyle i(t)={\frac {4}{3}}sin(3t)}
解答
假设初始平均功率为 0。实际上,这在逻辑上说不通。但每当计算积分时,都要考虑这种可能性。
v ( t ) = i ( t ) ∗ r {\displaystyle v(t)=i(t)*r} p ( t ) = i ( t ) ∗ v ( t ) = i ( t ) ∗ i ( t ) ∗ r = i ( t ) 2 ∗ r {\displaystyle p(t)=i(t)*v(t)=i(t)*i(t)*r=i(t)^{2}*r} p a v g = 1 t ∫ 0 t τ ∗ i ( τ ) 2 ∗ r d τ {\displaystyle p_{avg}={\frac {1}{t}}\int \limits _{0}^{t}{\tau }*i({\tau })^{2}*r\,d{\tau }} t = 2 π 3 {\displaystyle t={\frac {2\pi }{3}}} p a v g = 20 ∗ 3 2 π ∫ 0 2 π 3 τ ∗ ( 4 3 s i n ( 3 τ ) ) 2 d τ = 8.36 w a t t s {\displaystyle p_{avg}={\frac {20*3}{2\pi }}\int \limits _{0}^{\frac {2\pi }{3}}{\tau }*({\frac {4}{3}}sin(3{\tau }))^{2}\,d{\tau }=8.36watts} wolfram
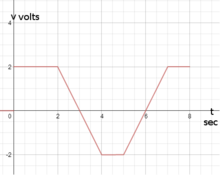
给定电压和电流的两个图像,求并绘制 t=0 到 t=8 的功率和能量图。
使用 desmos 创建 使用 desmos 创建 使用 desmos 创建 解答
将电压和电流图像转换为方程: v ( t ) , i ( t ) = { v = 0 , i = 0 , for t ≤ 0 v = 2 , i = 2 , for 0 < t ≤ 2 v = 2 − 2 ∗ ( t − 2 ) , i = − 2 , for 2 < t ≤ 4 v = − 2 , i = 2 , for 4 < t ≤ 5 v = 2 ∗ ( t − 5 ) − 2 , i = 2 , for 5 < t ≤ 6 v = 2 ∗ ( t − 5 ) − 2 , i = − 2 , for 6 < t ≤ 7 v = 2 , i = − 2 , for 7 < t ≤ 8 {\displaystyle v(t){\text{, }}i(t)={\begin{cases}v=0{\text{, }}i=0,&{\text{for }}t{\leq }0\\v=2{\text{, }}i=2,&{\text{for }}0<t{\leq }2\\v=2-2*(t-2){\text{, }}i=-2,&{\text{for }}2<t{\leq }4\\v=-2{\text{, }}i=2,&{\text{for }}4<t{\leq }5\\v=2*(t-5)-2{\text{, }}i=2,&{\text{for }}5<t{\leq }6\\v=2*(t-5)-2{\text{, }}i=-2,&{\text{for }}6<t{\leq }7\\v=2{\text{, }}i=-2,&{\text{for }}7<t{\leq }8\\\end{cases}}}
现在进行计算 p ( t ) = v ( t ) i ( t ) {\displaystyle p(t)=v(t)i(t)}
p ( t ) = { 0 , for t ≤ 0 4 , for 0 < t ≤ 2 4 ∗ ( t − 2 ) − 4 , for 2 < t ≤ 4 − 4 , for 4 < t ≤ 5 4 ∗ ( t − 5 ) − 4 , for 5 < t ≤ 6 4 − 4 ∗ ( t − 5 ) , for 6 < t ≤ 7 − 4 , for 7 < t ≤ 8 {\displaystyle p(t)={\begin{cases}0,&{\text{for }}t{\leq }0\\4,&{\text{for }}0<t{\leq }2\\4*(t-2)-4,&{\text{for }}2<t{\leq }4\\-4,&{\text{for }}4<t{\leq }5\\4*(t-5)-4,&{\text{for }}5<t{\leq }6\\4-4*(t-5),&{\text{for }}6<t{\leq }7\\-4,&{\text{for }}7<t{\leq }8\\\end{cases}}}
现在进入更困难的部分。 能量 w ( t ) = ∫ 0 t τ ∗ p ( τ ) d τ {\displaystyle w(t)=\int \limits _{0}^{t}{\tau }*p({\tau })\,d{\tau }} wolfram alpha 计算积分。
w ( t ) = { 0 , for t ≤ 0 ∫ 0 t 4 d τ = 4 t , for 0 < t ≤ 2 ∫ 2 t ( 4 ∗ ( τ − 2 ) − 4 ) d τ = 2 ( t 2 − 6 t + 8 ) , for 2 < t ≤ 4 ∫ 4 t ( − 4 ) d τ = − 4 ( t − 4 ) , for 4 < t ≤ 5 ∫ 5 t ( 4 ∗ ( τ − 5 ) − 4 ) d τ = 2 ( t 2 − 12 t + 35 ) , for 5 < t ≤ 6 ∫ 6 t ( 4 − ( τ − 5 ) ∗ 4 ) d τ = − 2 ( t − 6 ) 2 , for 6 < t ≤ 7 ∫ 7 t ( − 4 ) d τ = − 4 ( t − 7 ) , for 7 < t ≤ 8 {\displaystyle w(t)={\begin{cases}0,&{\text{for }}t{\leq }0\\\int \limits _{0}^{t}4\,d{\tau }=4t,&{\text{for }}0<t{\leq }2\\\int \limits _{2}^{t}(4*({\tau }-2)-4)\,d{\tau }=2(t^{2}-6t+8),&{\text{for }}2<t{\leq }4\\\int \limits _{4}^{t}(-4)\,d{\tau }=-4(t-4),&{\text{for }}4<t{\leq }5\\\int \limits _{5}^{t}(4*({\tau }-5)-4)\,d{\tau }=2(t^{2}-12t+35),&{\text{for }}5<t{\leq }6\\\int \limits _{6}^{t}(4-({\tau }-5)*4)\,d{\tau }=-2(t-6)^{2},&{\text{for }}6<t{\leq }7\\\int \limits _{7}^{t}(-4)\,d{\tau }=-4(t-7),&{\text{for }}7<t{\leq }8\\\end{cases}}}
从问题陈述中找到第一个初始条件。将起始时间 t 设置为初始条件,并找到积分常数。将 t 设置为定义段的结束值,找到下一个初始条件。
目标是找到累积能量,而不是每段能量的变化。这是通过确保前一段的终点值与下一段的起点值相匹配来实现的。在绘制图形时,不应该出现垂直跳跃。
w ( t ) = { 0 the assumed initial condition , for t ≤ 0 2 ( 0 ) 2 + C = 0 ⇒ C = 0 and 4 ∗ 2 + 0 = 8 , for 0 < t ≤ 2 2 ( 2 2 − 6 ∗ 2 + 8 ) + C = 8 ⇒ C = 8 and 2 ( 4 2 − 6 ∗ 4 + 8 ) + 8 = 8 , for 2 < t ≤ 4 − 4 ∗ ( 4 − 4 ) + C = 8 ⇒ C = 8 and − 4 ∗ ( 5 − 4 ) + 8 = 4 , for 4 < t ≤ 5 2 ∗ ( 5 2 − 12 ∗ 5 + 35 ) + C = 4 ⇒ C = 4 and 2 ( 6 2 − 12 ∗ 6 + 35 ) + 4 = 2 , for 5 < t ≤ 6 − 2 ( 6 − 6 ) 2 + C = 2 ⇒ C = 2 and − 2 ( 7 − 6 ) 2 + 2 = 0 , for 6 < t ≤ 7 − 4 ( 7 − 7 ) + C = 0 ⇒ C = 0 and − 4 ( 8 − 7 ) + 0 = − 4 , for 7 < t ≤ 8 {\displaystyle w(t)={\begin{cases}0{\text{ the assumed initial condition}},&{\text{for }}t{\leq }0\\2(0)^{2}+C=0\Rightarrow C=0{\text{ and }}4*2+0=8,&{\text{for }}0<t{\leq }2\\2(2^{2}-6*2+8)+C=8\Rightarrow C=8{\text{ and }}2(4^{2}-6*4+8)+8=8,&{\text{for }}2<t{\leq }4\\-4*(4-4)+C=8\Rightarrow C=8{\text{ and }}-4*(5-4)+8=4,&{\text{for }}4<t{\leq }5\\2*(5^{2}-12*5+35)+C=4\Rightarrow C=4{\text{ and }}2(6^{2}-12*6+35)+4=2,&{\text{for }}5<t{\leq }6\\-2(6-6)^{2}+C=2\Rightarrow C=2{\text{ and }}-2(7-6)^{2}+2=0,&{\text{for }}6<t{\leq }7\\-4(7-7)+C=0\Rightarrow C=0{\text{ and }}-4(8-7)+0=-4,&{\text{for }}7<t{\leq }8\\\end{cases}}}
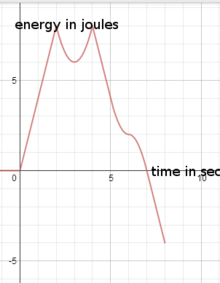
能量(焦耳)与时间(秒)的关系 desmos 绘制图形是检查工作的一种方式。没有图形,直观的分析过程就无法启动。
w ( t ) = { 0 , for t ≤ 0 4 t , for 0 < t ≤ 2 2 ( t 2 − 6 t + 8 ) + 8 , for 2 < t ≤ 4 − 4 ( t − 4 ) + 8 , for 4 < t ≤ 5 2 ( t 2 − 12 t + 35 ) + 4 , for 5 < t ≤ 6 − 2 ( t − 6 ) 2 + 2 , for 6 < t ≤ 7 − 4 ( t − 7 ) , for 7 < t ≤ 8 {\displaystyle w(t)={\begin{cases}0,&{\text{for }}t{\leq }0\\4t,&{\text{for }}0<t{\leq }2\\2(t^{2}-6t+8)+8,&{\text{for }}2<t{\leq }4\\-4(t-4)+8,&{\text{for }}4<t{\leq }5\\2(t^{2}-12t+35)+4,&{\text{for }}5<t{\leq }6\\-2(t-6)^{2}+2,&{\text{for }}6<t{\leq }7\\-4(t-7),&{\text{for }}7<t{\leq }8\\\end{cases}}}
在解决像这样长的问题时,建立直观理解很重要。 有两种基本方法可以做到这一点
思考电源的经验,并问“这意味着什么?”
添加预期感受和情绪。 思考经验、情绪、发生的事情,而不是你喜欢的最终结果。 将与它们相关的情绪与手头的问题联系起来。 将做这些事情与解决问题混合在一起。
讲一个故事,然后根据图表检查故事。 我们正在看什么类型的设备? 它必须是一个既消耗又产生电能的元件。 电流每两秒钟来回切换,因此它很可能是一个驱动某种来回运动的电机。 电机本质上是一个电感器。 电感器会改变电压,以试图保持电流恒定……就像一个电流源。 电机在最初的四秒钟内按计划工作(消耗能量)。 在接下来的四秒钟内,发生了其他事情。 看起来一个两岁的孩子抓住了试图来回振动的风扇,并迫使它朝相反的方向移动。 这会导致电机变成发电机,因此电压变化,负能量和功率。