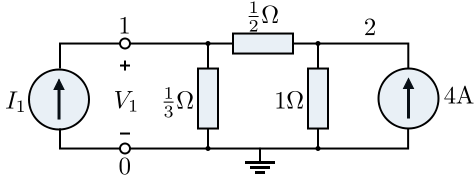电路理论/二端口网络

放大器是现存最有用的电路之一。它们几乎存在于每个电子设备中，从收音机和电视到洗衣机和示波器。它们构成了几乎所有更复杂电路的基础。放大器是一种接收输入并输出与其成比例（但不一定更大）的设备。我们可以将此表示为一个二端口电路，它具有一个输入端口和一个输出端口。

首先，让我们考虑我们已经熟悉的一端口电路

基本电路元件，如电阻器、电容器、电感器和独立电源，构成了最基本的一端口电路。更一般地，一个一端口电路可以包含任意数量的无源元件、独立和受控电源以及节点。通常，一旦设计了这些电路之一，我们就不再关心它是如何工作的，并很乐意用它在端口处的行为来表示它。通过使用我们已经学习的技术，我们可以将其简化为一个戴维宁或诺顿等效电路。

现在，考虑下面的二端口电路

某些器件具有超过两个端子，例如具有三个端子的 BJT 和具有三个或四个端子的 MOSFET。在这些情况下，无法将其表示为一端口电路，二端口电路是唯一的选择。二端口电路与一端口电路具有相同的应用，即它们允许我们只考虑电路的行为，而不是不必要的内部细节。

一端口电路回顾

在本节中，我们将再次研究一端口电路，并考虑一种更系统的方法来寻找诺顿和戴维宁等效电路。

示例 1

考虑以下电路

让我们计算由节点 $a$ 和 $b$ 构成的端口看进去的戴维宁和诺顿等效电路。为了找到开路电压，我们使用电流分配规则找到流过 1/3 Ω 电阻器的电流，并乘以 1/3

$v_{oc}={\frac {1}{{\frac {1}{2}}+{\frac {1}{3}}+1}}\times 4\times {\frac {1}{3}}={\frac {8}{11}}{\mbox{ V}}$

通过停用电流源并找到相应的阻抗来找到等效电阻

$R_{eq}={\frac {{\frac {1}{3}}\times \left({\frac {1}{2}}+1\right)}{{\frac {1}{3}}+\left({\frac {1}{2}}+1\right)}}={\frac {3}{11}}\,\Omega$

短路电流可以按如下方式找到

$i_{sc}={\frac {v_{oc}}{R_{eq}}}={\frac {8}{3}}{\mbox{ A}}$

因此，我们有以下戴维宁和诺顿等效电路

戴维宁和诺顿电路是原始电路的简化：无论原始电路有多少个节点，等效电路只有两个（这里，0 和 1）。我们可以将此过程视为消除非端口端子节点（在本例中为节点 2）的过程。我们可以使用节点分析的系统方法来实现这一点。

为此，我们将节点 0 定义为参考节点，并在节点 0 和 1 之间放置一个测试电流源

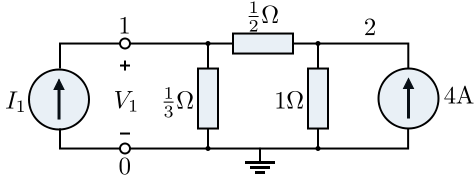
我们现在可以执行逐个检查的节点分析

${\begin{bmatrix}5&-2\\-2&3\end{bmatrix}}{\begin{bmatrix}V_{1}\\V_{2}\end{bmatrix}}={\begin{bmatrix}I_{1}\\4\end{bmatrix}}$

节点 2 不是端口节点，因此必须将其消除。我们可以使用高斯消元法来实现这一点。关于“3”进行主元操作

${\begin{bmatrix}5&-2\\-2&\mathbf {3} \end{bmatrix}}{\begin{bmatrix}V_{1}\\V_{2}\end{bmatrix}}={\begin{bmatrix}I_{1}\\4\end{bmatrix}}$

${\begin{bmatrix}5-{\frac {(-2)(-2)}{3}}\end{bmatrix}}{\begin{bmatrix}V_{1}\end{bmatrix}}={\begin{bmatrix}I_{1}-{\frac {(-2)4}{3}}\end{bmatrix}}$

${\begin{bmatrix}{\frac {11}{3}}\end{bmatrix}}{\begin{bmatrix}V_{1}\end{bmatrix}}={\begin{bmatrix}I_{1}+{\frac {8}{3}}\end{bmatrix}}$

此结果方程可以用电流或电压形式表示。

$I_{1}={\frac {11}{3}}V_{1}-{\frac {8}{3}}\quad {\mbox{or}}\quad V_{1}={\frac {3}{11}}I_{1}+{\frac {8}{11}}$

很明显，这些对应于我们之前找到的戴维南和诺顿等效电路。如果电路没有独立电源，我们只会得到一个对应于单个电阻的表达式。

示例 2

现在让我们考虑以下稍微复杂一点的例子。