曲柄式腿部机构比较/绘制 Jansen 联动机构
首先，我们需要一个带有常数的图形。
Theo Jansen 在他的网站上公布了这些数字：[1]（视频“The Legsystem”，3:36）或在网页的存档版本上：[2]
我建议命名这些点。命名可以是任意的。我使用了 Z..S 以避免与长度 a..m 混淆。
打印出图形并在上面涂鸦可能会非常有用。
现在我们必须考虑如何手工制作这个机构。
我们需要一个不可折叠的圆规、一把尺子、纸和一支铅笔。
-
不可折叠的圆规和尺子
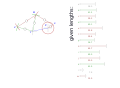
我们将原点 Z 设置为任意点。对于 Y，我们向下移动 l，向左移动 a。曲柄 m 可以处于任意角度。绘制曲柄会得到点 X。
从此点开始，我们构造由两点和两条长度定义的三角形。
在几何学中，这是 SSS 情况（根据三条边构造三角形，参见三角形解法#三条边给定（SSS））。
在纸上，这可以使用圆规轻松解决。
让我们从将圆规设置为长度 b 开始，然后将圆规放在点 Y 上。然后我们将圆规设置为长度 j，并将圆规放在点 X 上。弧线的交叉点是点 W。
请注意，当给出两点和两条长度时，总是存在两个解，即交叉点。鉴于我们已经知道机构的总体形状，我们知道需要哪一个。但请记住这一点以备后用。
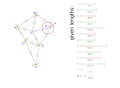
其余部分或多或少是“重复”。
- 长度用小写字母表示
- 点用大写字母表示
- 用于构造的线和弧线有一个'
- 构造点 Z
- 绘制水平线 h
- 绘制垂直线 v，与水平线 h 相交
- 标记 h 和 v 相交处的点 Z
- 这将是该构造的原点和腿部机构的曲柄轴
- 构造点 Y
- 从 h 向下绘制水平线 h'，距离为 l
- 从 v 向左绘制垂直线 v'，距离为 a
- 将 h' 和 v' 的交点标记为固定点 Y
- 构造点 X
- 通过 Z 绘制一条线 m'，添加一个任意角度（该角度是曲柄角度）
- 从点 Z 绘制半径为 m 的圆弧，圆弧 n 和点 Z 的交点是曲柄枢轴 X
- 从 Z 到 X 绘制线 m
- 构造点 W（SSS 情况）
- 从点 X 绘制半径为 j 的圆弧 j'
- 从点 Y 绘制半径为 b 的圆弧 b'
- 圆弧 j' 和 b' 的交点是点 W
- 从 X 到 W 绘制线 j
- 从 Y 到 W 绘制线 b
- 构造点 V（SSS 情况）
- 从点 W 绘制半径为 e 的圆弧 e'
- 从点 Y 绘制半径为 d 的圆弧 d'
- 从 W 到 V 绘制线 e
- 从 Y 到 V 绘制线 d
- 圆弧 e' 和 d' 的交点是点 V
- 构造点 U（SSS 情况）
- 从点 Y 绘制半径为 c 的圆弧 c'
- 从点 X 绘制半径为 k 的圆弧 k'
- 从 Y 到 U 绘制线 c
- 从 X 到 U 绘制线 k
- 圆弧 c' 和 k' 的交点是点 U
- 构造点 T（SSS 情况）
- 从点 V 绘制半径为 f 的圆弧 f'
- 从点 U 绘制半径为 g 的圆弧 g'
- 圆弧 f' 和 g' 的交点是点 T
- 从 V 到 T 绘制线 f
- 从 U 到 T 绘制线 g
- 构造点 S（SSS 情况）
- 从点 T 绘制半径为 h 的圆弧 h'
- 从点 U 绘制半径为 i 的圆弧 i'
- 圆弧 f' 和 g' 的交点是点 S
- 这是机构的“脚”
- 从 T 到 S 绘制线 h
- 从 U 到 S 绘制线 i
-
步骤 1 -
步骤 2 -
步骤 3 -
步骤 4 -
步骤 5 -
步骤 6 -
步骤 7 -
步骤 8
a=38.0
b=41.5
c=39.3
d=40.1
e=55.8
f=39.4
g=36.7
h=65.7
i=49.0
j=50.0
k=61.9
l= 7.8
m=15.0
Z fix point, origin, crank axis Y fix point X crank axis W V U T S foot
