控制系统/示例/二阶系统

二阶系统：示例

扫雷船上指向水听器阵列的阻尼控制系统，从传动轴到阵列的开环传递函数如下。

G(s)={\frac {K}{Js^{2}+K_{d}s}}

增益参数 K 可以改变。阵列的惯性矩 J 和水对阵列的粘性阻力产生的力 K_d 是已知常数，给出如下

该系统被安排为具有单位反馈的闭环系统。找到 K 的值，使得当输入为单位阶跃时，闭环响应的过冲量最多为 50%（大约）。您可以使用标准响应曲线。为了减少过冲量，K 应该大于还是小于该值？
找到系统相应的时域响应。
现在，系统接收恒定角速度 V 的输入。对于上面找到的 K 的极限值，计算 V 的最大值，使得阵列最多以 5° 的误差跟随输入。

首先，让我们绘制系统的框图。我们知道开环传递函数，并且存在单位反馈。因此，我们有

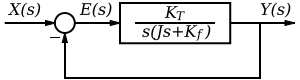
闭环增益由下式给出

$H(s)$	$={\frac {G(s)}{1+G(s)}}$
	$={\frac {\dfrac {K}{Js^{2}+K_{d}s}}{\dfrac {Js^{2}+K_{d}s+K}{Js^{2}+K_{d}s}}}$
	$={\frac {K}{Js^{2}+K_{d}s+K}}$

现在我们需要将闭环传递函数表示为标准二阶形式。

${\frac {\omega _{n}^{2}}{s^{2}+2\zeta \omega _{n}s+\omega _{n}^{2}}}$	$={\frac {K}{Js^{2}+K_{d}s+K}}$
	$={\frac {\frac {K}{J}}{s^{2}+{\frac {K_{d}}{J}}s+{\frac {K}{J}}}}$

现在我们可以表示自然频率 ω_n 和阻尼比 ζ

\omega _{n}^{2}={\frac {K}{J}}={\frac {K}{9}}

2\zeta \omega _{n}={\frac {K_{d}}{J}}

\zeta ={\frac {K_{d}}{2J}}{\sqrt {\frac {J}{K}}}={\frac {K_{d}}{2}}{\sqrt {\frac {1}{KJ}}}={\frac {1}{3{\sqrt {K}}}}

现在我们看看二阶系统的标准响应曲线。

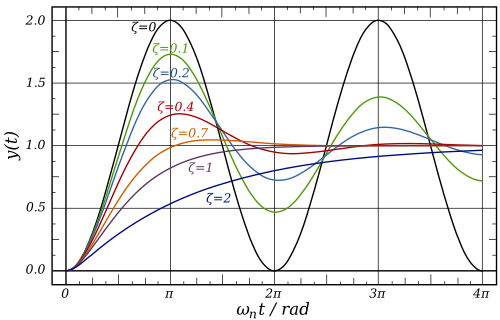
我们看到，对于 50% 的过冲，我们需要 ζ=0.2 或更大。

\zeta ={\frac {1}{3{\sqrt {K}}}}\geq {\frac {1}{5}}

K\leq {\frac {25}{9}}

这是允许的最大值，因此为了减少过冲，K 应该小于此值。现在我们可以完全评估自然频率。

\omega _{n}={\frac {5}{9}}

二阶系统的输出由以下等式给出。

$y(t)$	$=1-{\frac {1}{\sqrt {1-\zeta ^{2}}}}e^{-\zeta \omega _{n}t}\sin \left({\sqrt {1-\zeta ^{2}}}\omega _{n}t+\sin ^{-1}{\sqrt {1-\zeta ^{2}}}\right)$
	$=1-{\frac {1}{\sqrt {0.96}}}e^{-t/9}\sin \left({\frac {5{\sqrt {0.96}}}{9}}t+\sin ^{-1}{\sqrt {0.96}}\right)$
	$=1-1.02e^{-t/9}\sin \left(0.544t+0.436\pi \right)$