R 数据挖掘算法/聚类/自组织映射 (SOM)

简介

Kohonen 自组织特征映射 (SOFM 或 SOM) 是一种基于神经网络观点的聚类和数据可视化技术。与其他类型的基于中心点的聚类一样，SOM 的目标是找到一组中心点（在 SOM 术语中称为参考向量或码本向量）并将数据集中每个对象分配给最能近似该对象的中心点。在神经网络术语中，每个中心点都与一个神经元相关联 .

与增量式 K 均值一样，数据对象一次处理一个，并且更新最接近的中心点。与 K 均值不同的是，SOM 对中心点施加了地形排序，并且也会更新附近的中心点。点的处理会持续进行，直到达到某个预定的限制或中心点不再发生太大变化。SOM 技术的最终输出是一组隐式定义集群的中心点。每个集群包含最接近特定中心点的点 .

SOM 是一种聚类技术，它对生成的集群中心点实施邻域关系。因此，相邻的集群比不相邻的集群彼此更相关。这种关系有利于解释和可视化聚类结果。实际上，SOM 的这一方面已在许多领域得到利用，例如可视化 Web 文档或基因阵列数据 .

算法

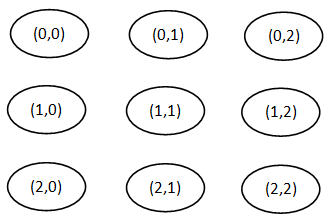
SOM 的一个区别特征是它对中心点（神经元）施加了地形（空间）组织。图 1 显示了一个二维 SOM 的示例，其中中心点由以矩形网格组织的节点表示。每个中心点都被分配了一对坐标（i，j）。有时，这样的网络以相邻节点之间的链接绘制，但这可能具有误导性，因为一个中心点对另一个中心点的影响是通过一个以坐标定义的邻域来实现的，而不是通过链接。SOM 神经网络有很多类型，但重点将放在二维 SOM 上，其中心点以矩形或六边形组织 .

图 1：二维 3x3 矩形 SOM 神经网络 .

尽管 SOM 与K 均值相似，但存在根本区别。SOM 中使用的中心点具有预定的地形排序关系。在训练过程中，SOM 使用每个数据点来更新最接近的中心点以及地形排序中附近的中心点。通过这种方式，SOM 为任何给定的数据集生成一组有序的中心点。换句话说，SOM 网格中彼此靠近的中心点比彼此更远的中心点彼此更相关。由于这个约束，二维 SOM 的中心点可以被视为位于试图尽可能好地拟合 n 维数据的二维表面上。SOM 中心点也可以被认为是非线性回归相对于数据点的结果。在高级别上，使用 SOM 技术的聚类包含以下算法中描述的步骤

1: Initialize the centroids.
2: repeat
3:    Select the next object.
4:    Determine the closest centroid to the object.
5:    Update this centroid and the centroids that are close, i.e., in a specified neighborhood.
6: until The centroids don't change much or a threshold is exceeded.
7: Assign each object to its closest centroid and return the centroids and clusters.

实现

对于 R（R 开发核心团队 2007 年），从综合 R 档案网络 (CRAN) 可以获得三个软件包，这些软件包实现了标准 SOM

• kohonen 软件包实现了自组织映射以及一些用于监督模式识别和数据融合的扩展。
• som 软件包提供了用于自组织映射的函数。
• wccsom 软件包用于比较具有峰值偏移的模式的 SOM 网络。

在本讨论中，重点放在kohonen 软件包上，因为它提供了 SOM 标准功能和顺序扩展。R 软件包kohonen 提供了用于自组织映射的函数。它还提供了两个扩展，允许将 SOM 用于分类和回归任务以及数据挖掘任务。它特别强调可视化。基本函数是：用于自组织映射的通常无监督形式的som；xyf 用于监督自组织映射和 XY 融合映射，当所有对象都具有额外信息（例如，类别变量）时，这很有用；bdk，一种称为双向 Kohonen 映射的替代公式；最后，从 2.0.0 版本开始，xyf 映射到超过两层信息的泛化，在函数supersom 中。这些函数可用于定义训练集中对象到映射单元的映射 .

kohonen 软件包中包含多个数据集：来自 UCI 机器学习资源库 的葡萄酒数据，来自 Wülfert 等人 (1998) 描述的乙醇、水和异丙醇三元混合物的近红外光谱，在不同温度下测量，最后是一组微阵列数据，来自 Spellman 等人 (1998) 的酵母数据。葡萄酒数据集包含有关来自三种不同葡萄品种的 177 个意大利葡萄酒样本的信息；已测量了 13 个变量（例如，酒精和黄酮类化合物的浓度，以及色调）。酵母数据是原始数据集的子集，包含 6178 个基因，这些基因被认为与酵母细胞周期有关。该数据集包含 800 个基因，使用六种不同的同步方法测量了这些基因的时间依赖性表达 .

不同类型的自组织映射可以通过调用函数som、xyf、bdk 或supersom 来获得，并将适当的数据表示作为第一个参数。其他几个参数提供了其他参数，例如映射大小、迭代次数等。返回的对象随后可用于检查、绘图、映射和预测。下面将展示软件包中提供的函数。可视化函数将在可视化主题中进行讨论 .

函数 som

函数som 实现了自组织映射的标准形式 .

som(data, grid=somgrid(), rlen = 100, alpha = c(0.05, 0.01), radius = quantile(nhbrdist, 0.67) * c(1, -1), init, 
toroidal = FALSE, n.hood,  keep.data = TRUE)  

参数是

• data: 一个矩阵，其中每行表示一个对象。
• grid: 代表的网格。
• rlen: 将完整数据集呈现给网络的次数。
• alpha: 学习率，一个包含两个数字的向量，指示变化量。默认情况下，从 0.05 线性下降到 0.01，跨越 rlen 次更新。
• 半径： 邻域的半径，可以是单个数字或向量（开始，结束）。 如果以单个数字给出，半径将从给定的数字运行到该数字的负值； 一旦邻域小于 1，只有获胜单元将被更新。 默认值为覆盖所有单元到单元距离的 2/3 的值。
• init： 初始代表，表示为矩阵。 如果缺失，则从“data”中随机选择（不放回）。
• toroidal： 如果为 TRUE，则地图的边缘相连。 请注意，在六边形环形地图中，行数必须为偶数。
• n.hood： 邻域的形状，可以是“circular”或“square”。 后者是矩形地图的默认值，前者是六边形地图的默认值。
• keep.data： 将数据保存在返回值中。

返回一个类为“kohonen”的对象，包含以下组件

• data： 数据矩阵，仅在 keep.data == TRUE 时返回。
• grid： 网格，一个类为“somgrid”的对象。
• codes： 代码向量的矩阵。
• changes： 代码向量平均偏差的向量。
• unit.classif： 所有数据对象的获胜单元，仅在 keep.data == TRUE 时返回。
• distances： 对象与其对应获胜单元之间的距离，仅在 keep.data == TRUE 时返回。
• toroidal： 是否使用环形地图。
• method： som 的类型，这里为“som”。

函数 xyf

函数 xyf 是自组织映射的监督版本，用于将高维光谱或模式映射到 2D 。

xyf(data, Y, grid=somgrid(), rlen = 100, alpha = c(0.05, 0.01), radius = quantile(nhbrdist, 0.67) * c(1, -1), 
xweight = 0.5, contin,  toroidal = FALSE, n.hood, keep.data = TRUE)

参数是

• data: 一个矩阵，其中每行表示一个对象。
• Y： 要建模的属性。 在分类的情况下，Y 是一个零矩阵，每行只有一个“1”，表示该类。 对于连续属性的预测，Y 是一个向量。 也可以进行组合，但应注意适当的缩放。
• grid: 代表的网格。
• rlen: 将完整数据集呈现给网络的次数。
• alpha: 学习率，一个包含两个数字的向量，指示变化量。默认情况下，从 0.05 线性下降到 0.01，跨越 rlen 次更新。
• radius： 邻域的半径，可以是单个数字或向量 start, stop)。 如果以单个数字给出，半径将从给定的数字运行到该数字的负值； 一旦邻域小于 1，只有获胜单元将被更新。 默认值为覆盖所有单元到单元距离的 2/3 的值。
• xweight： 在计算更新 Y 的距离时赋予 X 地图的权重。 默认值为 0.5。
• contin： 参数指示 Y 是连续的还是分类的。 默认值为检查 Y 的所有行和是否等于 1：在这种情况下，contin 为 FALSE。
• toroidal： 如果为 TRUE，则地图的边缘相连。 请注意，在六边形环形地图中，行数必须为偶数。
• n.hood： 邻域的形状，可以是“circular”或“square”。 后者是矩形地图的默认值，前者是六边形地图的默认值。
• keep.data： 将数据保存在返回值中。

返回一个类为“kohonen”的对象，包含以下组件

• data： 数据矩阵，仅在 keep.data == TRUE 时返回。
• Y： Y，仅在 keep.data == TRUE 时返回。
• contin： 参数指示 Y 是连续的还是分类的。
• grid： 网格，一个类为“somgrid”的对象。
• codes： 包含 X 和 Y 代码簿向量的两个矩阵的列表。
• changes： 包含两列代码向量平均偏差的矩阵。 第 1 列包含用于更新 Y 的偏差； 第 2 列包含用于更新 X 的偏差。
• toroidal： 是否使用环形地图。
• unit.classif： 所有数据对象的获胜单元，仅在 keep.data == TRUE 时返回。
• distances： 对象与其对应获胜单元之间的距离，仅在 keep.data == TRUE 时返回。
• method： som 的类型，这里为“xyf”。

函数 bdk

自组织映射的监督版本，用于将高维光谱或模式映射到 2D：双向 Kohonen 地图 。

bdk(data, Y, grid=somgrid(), rlen = 100, alpha = c(0.05, 0.01), radius = quantile(nhbrdist,0.67)
* c(1, -1), xweight = 0.75, contin, toroidal = FALSE, n.hood, keep.data = TRUE)

参数是

• data: 一个矩阵，其中每行表示一个对象。
• Y： 要建模的属性。 在分类的情况下，Y 是一个矩阵，每行只有一个“1”表示该类，其他地方为零。 对于连续属性的预测，Y 是一个向量。 也可以进行组合，但应注意适当的缩放。
• grid: 代表的网格。
• rlen: 将完整数据集呈现给网络的次数。
• alpha: 学习率，一个包含两个数字的向量，指示变化量。默认情况下，从 0.05 线性下降到 0.01，跨越 rlen 次更新。
• 半径： 邻域的半径，可以是单个数字或向量（开始，结束）。 如果以单个数字给出，半径将从给定的数字运行到该数字的负值； 一旦邻域小于 1，只有获胜单元将被更新。 默认值为覆盖所有单元到单元距离的 2/3 的值。
• xweight： 在计算更新 Y 的距离时赋予 X 地图的初始权重，以及在更新 X 时赋予 Y 地图的初始权重。 此权重将在训练期间线性降至 0.5。 默认值为 0.75。
• contin： 参数指示 Y 是连续的还是分类的。 默认值为检查 Y 的所有行和是否等于 1：在这种情况下，contin 为 FALSE。
• toroidal： 如果为 TRUE，则地图的边缘相连。 请注意，在六边形环形地图中，行数必须为偶数。
• n.hood： 邻域的形状，可以是“circular”或“square”。 后者是矩形地图的默认值，前者是六边形地图的默认值。
• keep.data： 将数据保存在返回值中。

返回一个类为“kohonen”的对象，包含以下组件

• data： 数据矩阵，仅在 keep.data == TRUE 时返回。
• Y： Y，仅在 keep.data == TRUE 时返回。
• contin： 参数指示 Y 是连续的还是分类的。
• grid： 网格，一个类为“somgrid”的对象。
• codes： 包含 X 和 Y 代码簿向量的两个矩阵的列表。
• changes： 包含两列代码向量平均偏差的矩阵。 第 1 列包含用于更新 Y 的偏差； 第 2 列包含用于更新 X 的偏差。
• toroidal： 是否使用环形地图。
• unit.classif： 所有数据对象的获胜单元，仅在 keep.data == TRUE 时返回。
• distances： 对象与其对应获胜单元之间的距离，仅在 keep.data== TRUE 时返回。
• method： som 的类型，这里为“bdk”。

函数 supersom

xyf 地图的扩展，用于多个数据层，这些数据层可能具有不同的变量数量（但对象数量相同） 。

supersom(data, grid=somgrid(), rlen = 100, alpha = c(0.05, 0.01), radius = quantile(nhbrdist, 0.67) * c(1, -1), contin, 
toroidal = FALSE,  n.hood, whatmap = NULL, weights = 1, maxNA.fraction = .5, keep.data = TRUE)

参数是

• data： 数据矩阵的列表。
• grid： 代表的网格：参见 somgrid。
• rlen: 将完整数据集呈现给网络的次数。
• alpha: 学习率，一个包含两个数字的向量，指示变化量。默认情况下，从 0.05 线性下降到 0.01，跨越 rlen 次更新。
• 半径： 邻域的半径，可以是单个数字或向量（开始，结束）。 如果以单个数字给出，半径将从给定的数字运行到该数字的负值； 一旦邻域小于 1，只有获胜单元将被更新。 默认值为覆盖所有单元到单元距离的 2/3 的值。
• contin： 参数指示数据是连续的还是分类的。 默认值为检查所有行和是否等于 1：在这种情况下，contin 为 FALSE。
• toroidal： 如果为 TRUE，则地图的边缘相连。 请注意，在六边形环形地图中，行数必须为偶数。
• n.hood： 邻域的形状，可以是“circular”或“square”。 后者是矩形地图的默认值，前者是六边形地图的默认值。
• whatmap： 对于 supersom 地图：在映射中使用哪些层。
• weights： 赋予各个层的权重。 默认值为 1/n，其中 n 是层的数量。
• maxNA.fraction： 允许为 NA 的值的最大比例，以防止删除行或列。
• keep.data： 将数据保存在返回值中。

返回一个类为“kohonen”的对象，包含以下组件

• data： 数据矩阵，仅在 keep.data == TRUE 时返回。
• contin： 参数指示数据元素是连续的还是分类的。
• na.rows： 由于至少一个层具有太多 NA，因此删除的对象（行）的索引。
• unit.classif： 所有数据对象的获胜单元，仅在 keep.data == TRUE 时返回。
• distances： 对象与其对应获胜单元之间的距离，仅在 keep.data == TRUE 时返回。
• grid： 网格，一个类为 somgrid 的对象。
• codes： 包含代码簿向量的矩阵列表。
• changes： 代码向量平均偏差的矩阵； 每张地图对应一列。
• toroidal： 是否使用环形地图。
• n.hood： 邻域的形状，可以是“circular”或“square”。 后者是
• 矩形地图的默认值，前者是六边形地图的默认值。
• weights： 对于 supersom 地图：映射中使用的层的权重。
• whatmap： 对于 supersom 地图：在映射中使用哪些层。
• method： 地图类型，这里为“supersom”。

函数 predict.kohonen

将对象映射到训练过的 Kohonen 地图，并为每个对象返回与其对应获胜单元相关的属性 。

## S3 method for class 'kohonen':
predict(object, newdata, trainX, trainY, unit.predictions, threshold = 0, whatmap = NULL, weights = 1, ...)

参数是

• object： 训练过的网络。
• newdata： 要进行预测的数据矩阵。 如果未给出，则默认为训练数据（如果可用）。
• trainX： 用于获取无监督地图预测的训练数据； 对于使用 keep.data = FALSE 选项训练的 som 地图来说是必需的。
• trainY： 训练数据的因变量的值； 对于 som 和 supersom 地图来说是必需的。
• unit.predictions： 每个单元预测值的可能覆盖。
• threshold： 在类预测中使用； 参见 classmat2classvec。
• whatmap： 对于 supersom 地图：在映射中使用哪些层。
• weights： 对于 supersom 地图：映射中使用的层的权重。
• ...： 目前未使用。

返回一个包含以下组件的列表

• prediction： 对感兴趣属性的预测值。 当预测多个值时，此元素是一个列表，否则是一个向量或矩阵。
• unit.classif： 数据矩阵中对象映射到的单元编号。
• unit.predictions： 与地图单元相关的平均值。 再次，当预测多个属性时，这是一个列表。

函数 classvec2classmat

将分类向量转换为矩阵或反之亦然 。

classvec2classmat(yvec)
classmat2classvec(ymat, threshold=0)

参数是

• yvec： 类向量。 通常是整数值，但也允许其他类型。
• ymat： 类矩阵：每列对应一个类。
• threshold： 仅在概率大于此阈值时才分类到一个类中。

返回

• classvec2classmat： 返回分类矩阵，其中每列由零和一组成。
• classmat2classvec： 返回一个类向量（整数）。

函数 check.whatmap

检查 whatmap 参数的有效性 。

check.whatmap(x, whatmap)

参数是

• x： 或者是一个来自 supersom 的 kohonen 对象，或者是一个可以作为 supersom 输入数据的 data 矩阵列表。
• whatmap： 数据子集的指示； 可以通过命名元素或给出索引来实现。 如果 whatmap 等于 NULL，则不执行任何选择。

返回

• 返回一个包含所选层的索引的数值向量。

函数 map.kohonen

将数据矩阵映射到训练过的 SOM 。

## S3 method for class 'kohonen':
map(x, newdata, whatmap = NULL, weights, scale.distances = (nmaps > 1), ...)

参数是

• x： 来自函数 som、xyf 或 bdk 的训练过的监督或无监督 SOM。
• newdata： 数据矩阵，行对应于对象。
• whatmap： 对于 supersom 地图：要考虑的层。
• weights： 对于 supersom 地图：用于映射的层的权重。
• scale.distances: 如果使用超 SOM 地图，是否按层重新缩放距离（默认）：如果为 TRUE，则每层的最大距离等于 1。如果应使用每层的距离的绝对值，则此参数应设置为 FALSE。请注意，在这种情况下，当映射训练数据时，由 map.kohonen 返回的结果将与地图中存在的映射不同。
• ...: 目前忽略。

返回一个包含以下元素的列表

• unit.classif: 与数据矩阵中的对象最接近的单元的向量。
• dists: 对象到单元的距离（目前仅限欧几里得距离）。
• whatmap,weights,scale.distances: 用于这些参数的值。

函数 unit.distances

计算 SOM 中单元之间的距离。

unit.distances(grid, toroidal)

参数是

• grid: somgrid 类的对象。
• toroidal: 如果为真，则地图的边缘连接起来，使拓扑成为环面。

返回

• 返回一个包含距离的（对称）矩阵。当 grid$n.hood 等于“circular”时，使用欧几里得距离；对于 grid$n.hood 为“square”则为最大距离。如果 toroidal 等于 TRUE，则地图在边缘连接，并为最短路径计算距离。

函数 tricolor

该函数以这样一种方式为 SOM 单元提供颜色值，即颜色在每个方向上平滑变化。

tricolor(grid, phis = c(0, 2 * pi/3, 4 * pi/3), offset = 0)

参数是

• grid: somgrid 类的对象，例如 kohonen 对象中的网格元素。
• phis: 三个旋转角度的向量。分别使用这些三个角度旋转后，单元的 y 坐标给出红色、绿色和蓝色的值。默认值对应于顶行中间单元的（近似）红色，以及底部左侧和右侧单元的纯绿色和蓝色。如果是三角形地图，则顶部的单元为纯红色。
• offset: 定义 RGB 颜色定义中的最小值（默认值为 0）。通过提供 [0, .9] 范围内的值，提供类似柔和的颜色。

返回

• 返回一个包含三列的矩阵，分别对应于红色、绿色和蓝色。这可以在 rgb 函数中使用，为单元提供颜色。

查看

在训练阶段之后，可以使用多个绘图函数进行可视化；该包可以显示对象的映射位置，具有多种可视化地图单元代码本向量的选项，并提供评估训练进度的方法。所有 SOM 类型都存在摘要函数。此外，可以轻松地将新数据投影到训练过的地图中；这提供了属性估计的可能性。

函数 summary 和 print

kohonen 对象的 summary 和 print 方法。print 方法显示地图的维度和拓扑；如果包含有关训练数据的的信息，则 summary 方法还会打印有关数据大小和对象与其最接近的代码本向量的平均距离的信息，这是映射质量的指标。

## S3 method for class 'kohonen':
summary(object, ...)
## S3 method for class 'kohonen':
print(x, ...)

参数是

• x, object: 一个 kohonen 对象
• ...: 未使用。

返回

图 2：函数 print 返回的有关葡萄酒数据的的信息

图 3：函数 summary 返回的有关葡萄酒数据的的信息

函数 plot.kohonen

绘制从 kohonen 函数获得的自组织地图。支持多种类型的绘图。

## S3 method for class 'kohonen':
plot(x, type = c("codes", "changes", "counts", "dist.neighbours", "mapping", "property", "quality"), classif = NULL, 
labels = NULL, pchs =  NULL, main = NULL, palette.name = heat.colors, ncolors, bgcol = NULL, zlim = NULL, heatkey = TRUE, 
property, contin, whatmap = NULL, codeRendering = NULL, keepMargins = FALSE, heatkeywidth = .2, ...)

参数是

• x: kohonen 对象。
• type: 绘图类型。
• classif: 分类对象（由 predict.kohonen 返回）或单元编号向量。仅当 type 等于“mapping”和“counts”时才需要。
• labels: 当 type 等于“mapping”时要绘制的标签。
• pchs: 当 type 等于“mapping”时要绘制的符号。
• main: 绘图的标题。
• palette.name: 用作“codes”、“counts”、“prediction”、“property”和“quality”绘图类型中单元背景的颜色。
• ncolors: 用于单元背景的颜色数量。对于连续数据，默认为 20；对于分类数据，默认为不同值的个数（如果少于 20）。
• bgcol: 可选参数，用于为“mapping”和“codes”绘图类型中的单元背景着色。分别默认为“gray”和“transparent”。
• zlim: 单元背景颜色编码的可选范围。
• heatkey: 是否在“property”和“counts”绘图类型中在绘图的左侧生成热键。
• property: 与“property”绘图类型一起使用的值。
• contin: 数据是否应被视为离散的（即类别）或连续的。仅与监督网络的绘图的颜色键相关。
• whatmap: 对于超 SOM 地图和“codes”绘图：要显示的地图。
• codeRendering: 如何显示代码。可能的选项：“segments”、“stars”和“lines”。
• keepMargins: 如果为 FALSE（默认），则在绘制 kohonen 地图后恢复原始图形参数。如果为 TRUE，则保留地图坐标系，以便可以使用 identify 函数向绘图添加符号或映射单元编号。
• Heatkeywidth: 颜色键的宽度；默认为 0.2，在大多数情况下应该可以工作，但在某些情况下（例如，绘制多个图形时）可能需要调整。
• ...: 其他图形参数，例如“mapping”绘图类型中的标签颜色或绘图符号。

支持多种类型的绘图

• "changes": 显示训练过程中与最接近的代码本向量的平均距离。
• "codes": 显示代码本向量。
• "counts": 显示映射到各个单元的对象数量。空单元用灰色表示。
• "dist.neighbours": 显示到所有直接邻居的距离之和。这种可视化也被称为 U 矩阵图。可以预期类边界附近的单元与其邻居的平均距离更大。目前仅适用于“som”和“supersom”地图。
• "mapping": 显示对象的映射位置。它需要“classif”参数，以及“labels”或“pchs”参数。
• "property": 可以计算每个单元的属性并用颜色代码显示。它可以用来可视化一个特定对象与地图中所有单元的相似性，显示所有单元和映射到它们的对象的平均相似性等等。参数 property 包含数值。
• "quality": 显示映射到一个单元的对象与其代码本向量的平均距离。距离越小，对象在代码本向量中表示的越好。

返回

图 4：左侧：使用 type 为“counts”调用该函数。右侧：使用 type 为“quality”调用该函数。

图 5：使用 type 为“property”调用函数 Plot。

图 6：使用 type 为“codes”调用函数 Plot。

图 7：使用 type 为“mapping”调用函数 Plot。

图 8：使用 type 为“changes”调用函数 Plot。

案例研究

在本节中，我们将说明使用 Kohonen 包的案例研究。

场景

自组织地图的标准形式在 som 函数中实现。要将 177 个样本的葡萄酒数据集映射到一个 5x4 的六边形单元地图上，可以使用 som 函数。首先，加载包（从现在开始，我们假设包已加载），然后加载数据，随后进行自动缩放，因为范围差异很大（特别是脯氨酸浓度，变量 13，有偏差）。第十四个变量是一个类别变量，不在映射中使用；它将在稍后用于可视化目的。

输入数据

作为输入数据，我们使用 kohonen 包中包含的 wine 数据集。该数据集包含 177 行和 13 列；对象 vintages 包含类别标签。为了与旧版本的包兼容，变量 wine.classes 也被保留下来。这些数据是化学分析结果，分析了在意大利同一地区（皮埃蒙特）种植的葡萄酒，但来自三种不同的葡萄品种：内比奥罗、巴巴雷斯科和格里尼奥利诺。用内比奥罗葡萄酿造的葡萄酒被称为巴罗洛。这些数据包含在三种葡萄酒中发现的多种成分的含量，以及一些光谱变量。

执行

以下代码可用于从数据集创建地图。请注意，首先，您需要加载包，然后加载数据集。

> library("kohonen")
Loading required package: class
> data("wines")
> wines.sc <- scale(wines)
> set.seed(7)
> wine.som <- som(data = wines.sc, grid = somgrid(5, 4, "hexagonal"))
> plot(wine.som, main = "Wine data")

输出

结果如图 9 所示。码本向量在段图中可视化，这是默认的绘图类型。例如，高酒精含量与投影在地图右下角的葡萄酒样本相关联，而颜色强度在左下角最大 .

图 9：5x4 映射的葡萄酒数据码本向量的图 .

分析

训练结果，wine.som 对象，是一个列表。最重要的元素是 codes 元素，它包含码本向量作为行。另一个值得检查的元素是 changes，这是一个向量，指示训练期间对码本向量的适应大小。这可以用来评估迭代次数是否足够 .

额外

下面显示了使用包中包含的 NIR 数据的示例：对于每种三元混合物，我们都有一个近红外光谱，以及三种化学物质的浓度（总和为 1）。此外，每个样品在五个不同的温度下测量。下面示例的目标是对水含量（三种浓度中的第二种）进行建模。在三种化学物质中，水对 NIR 光谱的影响最大。我们首先加载数据并附加数据框，以便 spectra、composition 和 temperature 对象直接可用。参数 xweight 指示赋予 X 多大重要性；这里它设置为 0.5（X 和 Y 同样重要），也是 xyf 中的默认值 .

> data("nir")
> attach(nir)
> set.seed(13)
> nir.xyf <- xyf(data = spectra, Y = composition[,2], xweight = 0.5, grid = somgrid(6, 6, "hexagonal"))
> par(mfrow = c(1, 2))
> plot(nir.xyf, type = "counts", main = "NIR data: counts")
> plot(nir.xyf, type = "quality", main = "NIR data: mapping quality")

这导致如图 4 所示的输出。在左侧图中，单元的背景颜色对应于映射到该特定单元的样本数量；它们在整个地图上合理地分布。四个单元是空的：没有样本被映射到它们。右侧图显示了映射到特定单元的对象到该单元码本向量的平均距离。一个好的映射应该在整个地图上显示很小的距离 .