数字电路/逻辑运算

数字电路

在上一章中，我们学习了什么是数字信息。数字信息用比特表示，可以取 1 或 0 的值。在本章中，我们将开始探讨如何使用数字信息进行计算和其他操作。

我们即将讨论的许多内容都是由乔治·布尔 (1815-1864) 在其 1854 年发表的论文 思想规律探究，逻辑与概率数学理论的基础 中正式化的。当时它几乎没有应用，但最终科学家和工程师意识到他的系统可以用来创建高效的计算机逻辑。涉及数字逻辑的数学分支被恰当地命名为布尔代数。

基本运算符

数字逻辑有三个基本运算符，与、或和非。这三个运算符构成了数字逻辑中一切的基础。事实上，您计算机执行的几乎所有操作都可以用这三个运算来描述。幸运的是，这些运算并不难理解，因为它们的含义类似于日常语言中这些词的含义。

与

与运算符的符号是一个点。使用与的数学表达式如下所示。

$A\cdot B$

与的另一种表示法是 $AB,A*B,A$ && $B$ 和 $A\land B.$ 只有当两个输入值都为 1 时，与表达式的值为 1。否则，值为 0。也就是说，只有当 A **和** B 为 1 时，上述表达式才等于 1。与运算符可以用以下真值表来描述。

$A$	$B$	$A\cdot B$
0	0	0
0	1	0
1	0	0
1	1	1

或

或运算符的符号是加号。使用或的数学表达式如下所示。

$A+B$

或的另一种表示法是 A $\vee$ B、A 或 B 以及 A || B。只有当两个输入值都为 0 时，或表达式的值为 0。否则，值为 1，也就是说，只有当 A 和 B 为 0 时，上述表达式才等于 1。或运算符的真值表

$A$	$B$	$A+B$
0	0	0
0	1	1
1	0	1
1	1	1

非

非是一个一元运算符，只需要单个输入，而与和或是二元运算符，因为它们需要两个值作为输入。非运算符的符号。 ${\overline {A}}$ 或 **A'**

非表达式的值为输入值的相反值。

$A$		${\overline {A}}$
0		1
1		0

与非和或非

如果将与、或和非运算符组合起来，就可以创建或非和与非

A 与非 B 是 ${\overline {A\cdot B}}$ 。这就是与门的反转输出。
A 或非 B 是 ${\overline {A+B}}$ 。这只是或门的反转输出。

与非

或非

Q={\overline {X\cdot Y}}

Q={\overline {X+Y}}

X	Y	Q
0	0	1
0	1	1
1	0	1
1	1	0

X	Y	Q
0	0	1
0	1	0
1	0	0
1	1	0

异或 (XOR) 和异或非 (XNOR)

另外两个重要的门是异或门和异或非门，分别用 XOR 和 XNOR 表示。这有时用一个圆圈中的加号表示。

A XOR B 是 ${\overline {A}}\cdot B+A\cdot {\overline {B}}=A\oplus B$ 。只有当输入中只有一个为 1 时，此结果才为真。
A XNOR B 是 ${\overline {{\overline {A}}\cdot B+A\cdot {\overline {B}}}}={\overline {A\oplus B}}$ 。这是异或门的反转输出：只有当两个输入相同的时候才为真。

XOR

XNOR

Q={X\oplus Y}

Q={\overline {X\oplus Y}}

X	Y	Q
0	0	0
0	1	1
1	0	1
1	1	0

X	Y	Q
0	0	1
0	1	0
1	0	0
1	1	1

XOR 代表模 2 加法，这意味着如果你将 1 加到 1，你将回到 0。这是数字电子学中非常有用的函数，但在布尔代数中它不是一个重要的概念。

形式数学运算符

在逻辑领域（它是离散数学的一部分），存在一种与我们所见过的加法/乘法类型不同的符号表示法。

AND 用 $\wedge$ 表示。因此A AND B将被写成 $A\wedge B$ 。
OR 用 $\vee$ 表示。因此A OR B将被写成 $A\vee B$ 。
NOT 用 $\lnot$ 表示。因此NOT A是 $\neg A$ 。

不幸的是，计算机科学、工程学和数学似乎无法达成共识，因此我们必须同时使用两种符号表示法。其他书籍，尤其是那些更侧重于纯逻辑或离散数学的书籍，可能使用各种不同的符号表示法，因此如果查阅其他书籍，则需要了解其他符号表示法。由于这是一本工程学书籍，我们不会使用这种符号表示法。

布尔代数定律

布尔代数与普通代数一样，也遵循一定的规则。这些规则是结合律、分配律、交换律和德摩根定律。结合律、交换律和分配律只适用于 AND 和 OR 运算符。其中一些定律可能看起来很琐碎，因为你已经习惯了它们。然而，当布尔代数被创建时，它拥有不同的规则，我们认为“正常”代数中理所当然的每一个公理都无法保证适用。这些定律已被证明在布尔代数下成立。

结合律

维基百科在 结合律 中有相关信息

结合律是代数中的一种性质，表示项的求值顺序无关紧要。

A+(B+C)\iff (A+B)+C\,

A\cdot (B\cdot C)\iff (A\cdot B)\cdot C\,

分配律

维基百科在 分配律 有相关信息

分配律是指运算符可以应用于括号内的每个项。

A\cdot (B+C)\iff (A\cdot B)+(A\cdot C)\,

A+(B\cdot C)\iff (A+B)\cdot (A+C)\,

交换律

维基百科在 交换律 有相关信息

交换律是指运算符应用的顺序无关紧要。

A\cdot B\iff B\cdot A\,

A+B\iff B+A\,

德摩根定律

维基百科在 德摩根定律 有相关信息

德摩根定律是 NOT 或非运算符不是分配律的结果。

{\overline {P\cdot Q}}\iff {\overline {P}}+{\overline {Q}}

{\overline {P+Q}}\iff {\overline {P}}\cdot {\overline {Q}}

德摩根定律（以奥古斯都·德·摩根 (Augustus De Morgan)，1806 年至 1871 年命名）告诉我们：一个与非门给出与输入取反的或门的相同输出；一个或非门给出与输入取反的与门的相同输出。这些输入取反的门也称为气泡门，因为它们在符号上的表示方式，即在每个输入上添加一个小的“气泡”，就像在 NOT、NAND 和 NOR 门的输出上画圆圈一样。

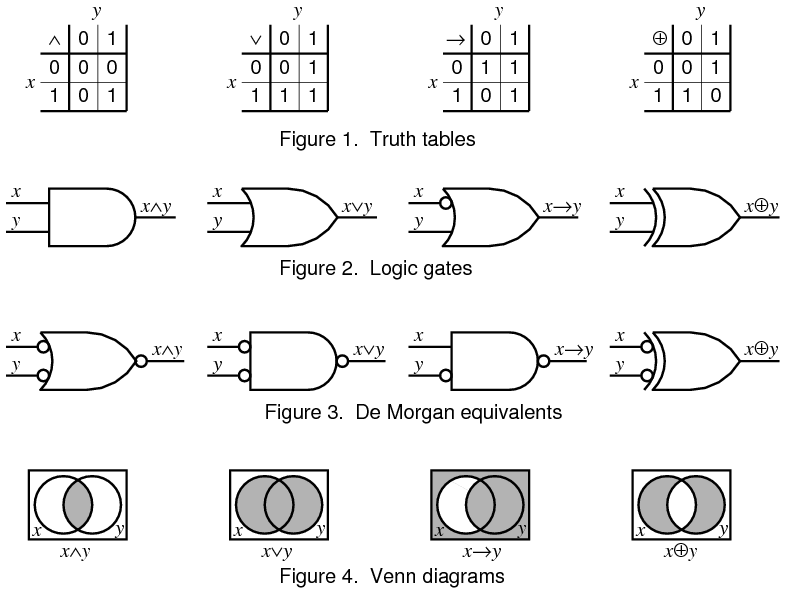
德摩根定律在简化布尔表达式时最有用。记住这些定律的一种简单方法是“改变符号，打断线”。

(练习索引)

练习

通过构建适当的真值表，验证以下定律：

与运算符的结合律，
或运算符的分配律，
或运算符的交换律，
与非运算符的德摩根定律。

解答

我们看到以下的真值表

运算符优先级

重要的是要注意

A\cdot B+C\neq A\cdot (B+C)

这可以看作是 AND 具有更高的优先级，或者与和或之间不满足结合律，或者是对分配律的无效应用。

从另一个角度来看，这是我们对普通代数的理解的应用，其中将或类比于加法，将与类比于乘法。如果这是用数字而不是布尔实体的普通代数，我们永远不会犯这个错误。

其他规则

所有这些定律都导致了许多适用于所有布尔表达式的规则。这些定律有名字，但重要的是你能够在需要的时候应用它们！请注意，许多规则有两种形式 - 这称为对偶性，我们将在后面讨论。

	名称	规则
1a	幂等律	$A\cdot A=A\,$
1b	幂等律	$A+A=A\,$
2a	恒等律	$A+0=A\,$
2b	恒等律	$A\cdot 1=A\,$
3a	有界性	$A+1=1\,$
3b	有界性	$A\cdot 0=0\,$
4a	补定律	$A+{\overline {A}}=1\,$
4b	补定律	$A\cdot {\overline {A}}=0\,$
5a	吸收律	$A+(A\cdot B)=A\,$
5b	吸收律	$A\cdot (A+B)=A\,$
6	对合律或双重否定律	${\overline {\overline {\,A}}}=A$
7a	一致性定理	$A\cdot B+{\overline {A}}\cdot C+B\cdot C=A\cdot B+{\overline {A}}\cdot C$
7b	一致性定理	$(A+B)\cdot ({\overline {A}}+C)\cdot (B+C)=(A+B)\cdot ({\overline {A}}+C)$