数字信号处理/Σ-Δ调制

Σ-Δ调制器 (ΣΔ 调制器) 允许通过一位信号进行模拟到数字转换 (ADC) 或数字到模拟转换 (DAC) 操作。

脉冲宽度调制 (PWM) 也使用一位信号，但信噪比 (SNR) 更差，但切换速度更慢。

一阶调制器

电路

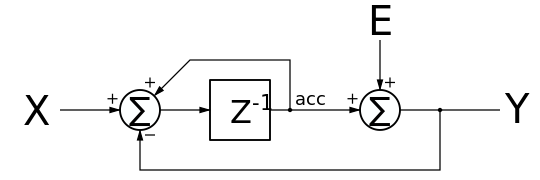
一阶 ΣΔ 调制器由累加器和比较器组成。

调制器 - 一阶 - 数字

输出是一个比特流，原始信号可以通过低通滤波器重建。

分析

可以通过用误差信号的加法替换比较器来分析 Σ-Δ 调制器的频率响应。

${\begin{array}{ccl}z\cdot acc&=&X+acc-Y\\Y&=&acc+E\end{array}}$

从这些等式中，可以找到信号传递函数 (STF)

${\frac {Y(z)}{X(z)}}={\frac {1}{z}}$

以及噪声传递函数 (NTF)

${\frac {Y(z)}{E(z)}}={\frac {z-1}{z}}$

STF 是一段时间的延迟，但 NTF 是一阶高通函数。这表明由于切换而产生的调制噪声占据了更高的频率。如果输入信号限制在低频，则可以使用低通滤波器将信号与噪声分离。由于高通传递函数随着频率降低而以 20 dB/十倍频程（或 6 dB/八度音程）降低，因此信噪比以相同的速率增加。将噪声幅度在信号频带内积分表明一阶调制器每八度音程获得 1.5 位的信噪比。这可以与 PCM 相比，PCM 每八度音程仅获得 1 位的增益。

当输入恒定时，一阶调制器将提供循环模式。对于特定的输入值，此模式可能变得非常长，这会导致调制信号中出现低频振铃音。由于这些音调的频率越来越低，因此越来越难以将它们与原始信号分离。高阶调制器显示的重复模式更少，因此比一阶调制器更受欢迎。

二阶调制器

电路

二阶 ΣΔ 调制器需要 2 个累加器。不同的拓扑结构是可能的。以下电路显示了一个典型的二阶电路。

这两个系数允许与相应的噪声整形特性一起控制数字到模拟的传递函数。

分析

同样，比较器可以被误差信号的插入所取代

NTF 和 STF 可以从以下等式中找到

${\begin{array}{ccrcccccccccc}z\cdot {\begin{bmatrix}acc_{1}\\acc_{2}\end{bmatrix}}&=&{\begin{bmatrix}1&0\\1&1\end{bmatrix}}&\cdot &{\begin{bmatrix}acc_{1}\\acc_{2}\end{bmatrix}}&+&{\begin{bmatrix}1\\0\end{bmatrix}}&\cdot &X&+&{\begin{bmatrix}-c_{1}\\-c_{2}\end{bmatrix}}&\cdot &Y\\Y&=&{\begin{bmatrix}0&1\end{bmatrix}}&\cdot &{\begin{bmatrix}acc_{1}\\acc_{2}\end{bmatrix}}&+&{\begin{bmatrix}0\end{bmatrix}}&\cdot &X&+&{\begin{bmatrix}1\end{bmatrix}}&\cdot &E\end{array}}$

可以改写为

${\begin{array}{ccccccc}z\cdot {\overrightarrow {acc}}&=&\mathbf {A} \cdot {\overrightarrow {acc}}&+&\mathbf {B} \cdot X&+&\mathbf {B_{y}} \cdot y\\Y&=&\mathbf {C} \cdot {\overrightarrow {acc}}&+&\mathbf {D} \cdot X&+&\mathbf {D_{e}} \cdot E\end{array}}$

信号传递函数

STF 是通过设置 $E=0$得到的：

${\begin{array}{ccccccc}z\cdot {\overrightarrow {acc}}&=&\mathbf {A} \cdot {\overrightarrow {acc}}&+&\mathbf {B} \cdot X&+&\mathbf {B_{y}} \cdot (\mathbf {C} \cdot {\overrightarrow {acc}}+\mathbf {D} \cdot X)\\Y&=&\mathbf {C} \cdot {\overrightarrow {acc}}&+&\mathbf {D} \cdot X\end{array}}$

这可以改写为状态空间表示:

${\begin{array}{ccccc}z\cdot {\overrightarrow {acc}}&=&(\mathbf {A} +\mathbf {B_{y}} \cdot \mathbf {C} )\cdot {\overrightarrow {acc}}&+&(\mathbf {B} +\mathbf {B_{y}} \cdot \mathbf {D_{e}} )\cdot X\\Y&=&\mathbf {C} \cdot {\overrightarrow {acc}}&+&\mathbf {D} \cdot X\end{array}}$

状态空间矩阵由调制矩阵 $\mathbf {A} ,\mathbf {B} ,\mathbf {B_{y}} ,\mathbf {C} ,\mathbf {D} ,\mathbf {D_{e}}$ 构成，如下所示：

${\begin{array}{l}A_{x}=(\mathbf {A} +\mathbf {B_{y}} \cdot \mathbf {C} )\\B_{x}=(\mathbf {B} +\mathbf {B_{y}} \cdot \mathbf {D} )\\C_{x}=\mathbf {C} \\D_{x}=\mathbf {D} \end{array}}$

求解二阶调制器的系统，得到：

${\frac {Y}{X}}={\frac {1}{z^{2}-(2-c_{2})z+(1+c_{1}-c_{2})}}$

噪声传递函数

通过令 $X=0$，可以得到 NTF：

${\begin{array}{ccccc}z\cdot {\overrightarrow {acc}}&=&\mathbf {A} \cdot {\overrightarrow {acc}}&+&\mathbf {B_{y}} \cdot (\mathbf {C} \cdot {\overrightarrow {acc}}+\mathbf {D_{e}} \cdot E)\\Y&=&\mathbf {C} \cdot {\overrightarrow {acc}}&+&\mathbf {D_{e}} \cdot E\end{array}}$

这可以改写为状态空间表示:

${\begin{array}{ccccc}z\cdot {\overrightarrow {acc}}&=&(\mathbf {A} +\mathbf {B_{y}} \cdot \mathbf {C} )\cdot {\overrightarrow {acc}}&+&\mathbf {B_{y}} \cdot \mathbf {D_{e}} \cdot E\\Y&=&\mathbf {C} \cdot {\overrightarrow {acc}}&+&\mathbf {D_{e}} \cdot E\end{array}}$

状态空间矩阵由调制矩阵 $\mathbf {A} ,\mathbf {B} ,\mathbf {B_{y}} ,\mathbf {C} ,\mathbf {D} ,\mathbf {D_{e}}$ 构成，如下所示：

${\begin{array}{l}A_{e}=(\mathbf {A} +\mathbf {B_{y}} \cdot \mathbf {C} )\\B_{e}=\mathbf {B_{y}} \cdot \mathbf {D_{e}} \\C_{e}=\mathbf {C} \\D_{e}=\mathbf {D_{e}} \end{array}}$

求解二阶调制器的系统，得到：

${\frac {Y}{X}}={\frac {(z-1)^{2}}{z^{2}-(2-c_{2})z+(1+c_{1}-c_{2})}}$

评论

矩阵 $\mathbf {A} ,\mathbf {B} ,\mathbf {B_{y}} ,\mathbf {C} ,\mathbf {D} ,\mathbf {D_{e}}$ 包含了模拟和分析任何Σ-Δ调制器行为的所有信息。从这些矩阵推导出NTF和STF的状态空间描述一般适用于任何Σ-Δ调制器。

矩阵 $\mathbf {A_{x}}$ 和 $\mathbf {A_{e}}$ 是相同的，这意味着STF和NTF具有相同的极点。STF只有极点，这导致了低通函数。NTF在 $Z=1$ 处有两个极点，这给出了高通响应。这确保了信号和噪声是可分离的。

STF的直流增益为

${\frac {Y}{X}}(Z=1)={\frac {1}{c_{1}}}$

通过将输入乘以$c_{1}$，可以实现 1 的 STF 直流增益。

设计

STF 的极点由下式给出

$p_{12}=(1-{\frac {c_{2}}{2}})\pm j{\sqrt {c_{1}-{\frac {c_{2}^{2}}{4}}}}$

这个方程允许任意地放置 STF 的极点。对于一对位于

$p_{12}=a\pm jb$

的极点，调制器系数为

${\begin{cases}{\begin{array}{ll}c_{1}&=(1-a)^{2}+b^{2}\\c_{2}&=2(1-a)\end{array}}\end{cases}}$

例如，一个截止频率为采样频率 1/4 的全极点巴特沃斯 STF 给出的极点为

$p_{12}=0.375\pm j0.320$

和系数

${\begin{cases}{\begin{array}{ll}c_{1}&=0.493\\c_{2}&=1.250\end{array}}\end{cases}}$

一个接近贝塞尔 STF 的全极点 STF，其截止频率约为采样频率的 1/4，给出的系数为

${\begin{cases}{\begin{array}{ll}c_{1}&=26/32\\c_{2}&=56/32\end{array}}\end{cases}}$

注意，使用系数$c_{1}=c_{2}=1$ 或 $c_{1}=c_{2}=1/2$ 的常规习惯会导致极点正好位于单位圆上，从稳定性的角度来看，这并不可取。

更高阶拓扑

对于更高阶调制器，存在不同的拓扑结构。

简化积分器链路反馈 (SCIFB)

下图显示了一个简化积分器链路反馈 (SCIFB) 调制器

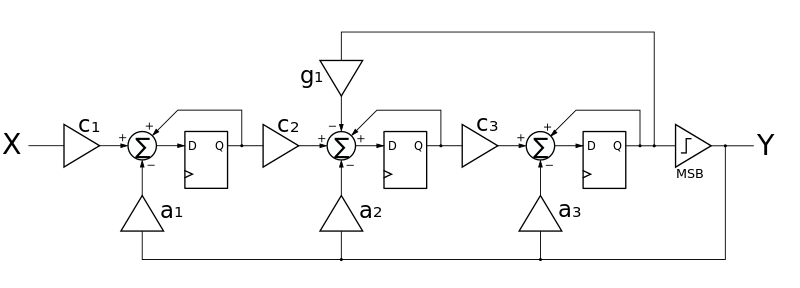SCIFB 调制器 - 阶数 3

当系数$g_{1}$ 不为零时，这是一个具有局部谐振器的结构。

对于这个结构，系统方程为

${\begin{array}{ccrcccccccccc}z\cdot {\begin{bmatrix}acc_{1}\\acc_{2}\\acc_{3}\end{bmatrix}}&=&{\begin{bmatrix}1&0&0\\c_{2}&1&-g_{1}\\0&c_{3}&1\end{bmatrix}}&\cdot &{\begin{bmatrix}acc_{1}\\acc_{2}\\acc_{3}\end{bmatrix}}&+&{\begin{bmatrix}c_{1}\\0\\0\end{bmatrix}}&\cdot &X&+&{\begin{bmatrix}-a_{1}\\-a_{2}\\-a_{3}\end{bmatrix}}&\cdot &Y\\Y&=&{\begin{bmatrix}0&0&1\end{bmatrix}}&\cdot &{\begin{bmatrix}acc_{1}\\acc_{2}\\acc_{3}\end{bmatrix}}&+&{\begin{bmatrix}0\end{bmatrix}}&\cdot &X&+&{\begin{bmatrix}1\end{bmatrix}}&\cdot &E\end{array}}$

矩阵如下：

${\begin{array}{ccc}A&=&{\begin{bmatrix}1&0&0\\c_{2}&1&-g_{1}\\0&c_{3}&1\end{bmatrix}}\end{array}}$

${\begin{array}{ccc}B&=&{\begin{bmatrix}c_{1}\\0\\0\end{bmatrix}}\end{array}}$

${\begin{array}{ccc}B_{y}&=&{\begin{bmatrix}-a_{1}\\-a_{2}\\-a_{3}\end{bmatrix}}\end{array}}$

${\begin{array}{ccc}C&=&{\begin{bmatrix}0&0&1\end{bmatrix}}\end{array}}$

${\begin{array}{ccc}D&=&{\begin{bmatrix}0\end{bmatrix}}\end{array}}$

${\begin{array}{ccc}D_{e}&=&{\begin{bmatrix}1\end{bmatrix}}\end{array}}$