信号处理/滤波器设计

滤波器设计

滤波器设计通常从其频率响应的规范开始。由此，必须选择传递函数和滤波器结构。实际上，某些滤波器结构（例如二阶段链）可适应任何滤波器函数，而基本梯形滤波器结构，其串联支路仅包含电感，并联支路仅包含电容，仅实现全极点低通传递函数。将传递函数映射到滤波器结构会给出模拟滤波器元素的元件值和数字滤波器的系数。

从理想滤波器开始，需要进行进一步的优化。

集中元件或系数值是理想值。集中元件值必须映射到现有组件的值。滤波器系数必须四舍五入到滤波器电路的数字表示支持的值。例如，选择定点或浮点数字信号处理器 (DSP) 将导致更粗略或更精细的系数值。

然后，必须考虑滤波器内部的信号幅度。对于有源滤波器和数字滤波器，必须检查内部信号是否发生饱和或溢出。对于任何滤波器，信号都不应变得太小，因为这会严重影响整个滤波器的信噪比。因此，基本上，滤波器设计过程不仅分析从输入到输出的传递函数，还分析从输入到内部信号的传递函数。

滤波器表示

滤波器可以用多种等效方式表示

显然是通过其传递函数
通过传递函数的零点和极点，以及增益因子
通过滤波器的状态空间表示

方法允许在一种表示形式之间切换。不同的表示形式对滤波器属性有特定的启示。传递函数，绘制为 $s=j\omega$ ，显示了频率如何被放大或衰减。零极点图直接提供系统稳定性的信息。状态空间表示更深入地了解所选择的滤波器结构，并允许分析滤波器内部某些信号（状态变量）的幅度。

传递函数

对于简单的滤波器（如低通、高通、带通或带阻），选择传递函数最常见的方法是选择一个常用的滤波器函数：巴特沃斯、切比雪夫、椭圆、贝塞尔等等。

可实现的传递函数采用两个多项式的商形式。

H(s)={\frac {num(s)}{den(s)}}

滤波器阶数是两个多项式中 $s$ （或对于采样系统中的 $z$ ）的最大幂。

4阶传递函数的形式为

H(s)={\frac {b_{4}s^{4}+b_{3}s^{3}+b_{2}s^{2}+b_{1}s+b_{0}}{a_{4}s^{4}+a_{3}s^{3}+a_{2}s^{2}+a_{1}s+a_{0}}}

4阶全极点传递函数的形式为

H(s)={\frac {1}{a_{4}s^{4}+a_{3}s^{3}+a_{2}s^{2}+a_{1}s+a_{0}}}

4阶FIR传递函数的形式为

H(z)={\frac {b_{4}z^{4}+b_{3}z^{3}+b_{2}z^{2}+b_{1}z+b_{0}}{1}}=b_{4}z^{4}+b_{3}z^{3}+b_{2}z^{2}+b_{1}z+b_{0}

大多数滤波器类型试图尽可能接近砖墙形状，但其优化目标不同。对于这些类型，滤波器阶数越高，函数越接近砖墙形状。巴特沃斯滤波器通过具有最大平坦（无纹波）的传递函数来实现这一点。另一方面，贝塞尔滤波器的目标是最小化通带中的群延迟变化。

这些传递函数是针对归一化低通滤波器定义的。滤波器变换技术允许将低通函数变换为具有所需截止频率的低通、高通、带通或带阻。

此外，这些函数代表时间连续系统，可通过拉普拉斯分析来理解。对于采样系统（例如，开关电容或数字滤波器），还需要一个额外的步骤： $s$ 为基础的传递函数需要转换为 $z$ 为基础的传递函数。

零点、极点和增益

零点是传递函数分子的根。极点是传递函数分母的根。增益是传递函数的直流值： $s=0$ 时的值。

由其零点 $z_{i}$ 、极点 $p_{i}$ 和增益 $k$ 给出的系统的传递函数为

H(s)=k\cdot {\frac {\prod _{i=1}^{M}(s-z_{i})}{\prod _{i=1}^{N}(s-p_{i})}}

一个稳定的线性时不变系统的所有极点都位于 $s$ 的左半平面（即，具有负实部）。

状态空间表示

状态空间表示将滤波器描述为一组微分方程

{\dot {\mathbf {x} }}(t)=A\cdot \mathbf {x} (t)+B\cdot u(t)

y(t)=C\cdot \mathbf {x} (t)+D\cdot u(t)

这里，输入是 $u(t)$ ，内部滤波器信号是 $\mathbf {x} (t)$ ，输出是 $y(t)$ 。这些方程的拉普拉斯变换由以下给出

s\cdot \mathbf {X} (s)=A\cdot \mathbf {X} (s)+B\cdot U(s)

Y(s)=C\cdot \mathbf {X} (s)+D\cdot U(s)

传递函数由下式给出：

H(s)={\frac {Y(s)}{U(s)}}=C(s\mathbf {I} -A)^{-1}B+D

$A$ 的特征值是系统的极点。 $A$ 的特征多项式是传递函数的分母。

例子

4 阶归一化巴特沃斯滤波器

例子

本示例将介绍 4 阶归一化巴特沃斯滤波器的不同表示形式。

与其他由多项式给出的滤波器函数相反，巴特沃斯滤波器最适合通过其极点的位置来描述。它是一个全极点函数：它没有零点。

极点

归一化的巴特沃斯滤波器在单位圆的左半平面部分具有等间距极点。对于 4 阶滤波器，它们的取值为

{\begin{cases}p_{1},p_{1}^{*}=e^{\pm i(\pi /2+\pi /8)}\\p_{2},p_{2}^{*}=e^{\pm i(\pi /2+3\pi /8)}\end{cases}}or{\begin{cases}p_{1},p_{1}^{*}=-0.383\pm 0.924\cdot i\\p_{2},p_{2}^{*}=-0.924\pm 0.383\cdot i\end{cases}}

传递函数

因此，传递函数为

H(s)={\frac {1}{(s-p_{1})\cdot (s-p_{1}^{*})\cdot (s-p_{2})\cdot (s-p_{2}^{*})}}

H(s)={\frac {1}{(s^{2}-2\cdot re(p_{1})\cdot s+1)\cdot (s^{2}-2\cdot re(p_{2})\cdot s+1)}}

H(s)={\frac {1}{(s^{2}+0.765s+1)\cdot (s^{2}+1.848s+1)}}

H(s)={\frac {1}{s^{4}+2.61s^{3}+3.41s^{2}+2.61s+1}}

状态空间表示

从传递函数中可以找到一个可能的状态空间表示

Y(s)=U(s){\frac {1}{s^{4}+2.61s^{3}+3.41s^{2}+2.61s+1}}

s^{4}\cdot Y(s)+2.61s^{3}\cdot Y(s)+3.41s^{2}\cdot Y(s)+2.61s\cdot Y(s)+Y(s)=U(s)

s\cdot s^{3}\cdot Y(s)=-Y(s)-2.61s\cdot Y(s)-3.41s^{2}\cdot Y(s)-2.61s^{3}\cdot Y(s)+U(s)

写作

{\begin{cases}X_{1}(s)=Y(s)\\X_{2}(s)=s\cdot Y(s)=s\cdot X_{1}(s)\\X_{3}(s)=s^{2}\cdot Y(s)=s\cdot X_{2}(s)\\X_{4}(s)=s^{3}\cdot Y(s)=s\cdot X_{3}(s)\\\end{cases}}

给出

s\cdot X_{4}(s)=-X_{1}(s)-2.61\cdot X_{2}(s)-3.41\cdot X_{3}(s)-2.61\cdot X_{4}(s)+U(s)

这可以被改写成矩阵形式

{\begin{matrix}s\cdot {\begin{bmatrix}X_{1}\\X_{2}\\X_{3}\\X_{4}\end{bmatrix}}&=&{\begin{bmatrix}0&1&0&0\\0&0&1&0\\0&0&0&1\\-1&-2.61&-3.41&-2.61\end{bmatrix}}{\begin{bmatrix}X_{1}\\X_{2}\\X_{3}\\X_{4}\end{bmatrix}}&+&{\begin{bmatrix}0\\0\\0\\1\end{bmatrix}}U\\Y&=&{\begin{bmatrix}1&0&0&0\end{bmatrix}}{\begin{bmatrix}X_{1}\\X_{2}\\X_{3}\\X_{4}\end{bmatrix}}&+&{\begin{bmatrix}0\end{bmatrix}}U\end{matrix}}

Octave 代码

以下Octave 代码提供相同的结果，并绘制了滤波器的幅频响应

> order = 4;
> [z, p, g] = butter(order, 1, 's')
    z = []  (0x0)
    p = -0.38268 + 0.92388i
        -0.92388 + 0.38268i
        -0.92388 - 0.38268i
        -0.38268 - 0.92388i
    g =  1

> [b, a] = butter(order, 1, 's')
    b =  1
    a = 1.0000   2.6131   3.4142   2.6131   1.0000

> w = logspace(-1, 1, 100);
> while ( length(b) < length(a) )
>   b = [0, b];
> endwhile;
> Adb = 20*log10(abs(freqs(b, a, w)));
> figure(1);
> semilogx(w, Adb);
> grid;
   An amplitude response plot appears in a Gnuplot window

> [A, B, C, D] = tf2ss(b, a)
    A = 0.00000   1.00000   0.00000   0.00000
        0.00000   0.00000   1.00000   0.00000
        0.00000   0.00000   0.00000   1.00000
       -1.00000  -2.61313  -3.41421  -2.61313

    B = 0
        0
        0
        1

    C = 1   0   0   0

    D = 0

> eig(A)
    ans = -0.38268 + 0.92388i
          -0.38268 - 0.92388i
          -0.92388 + 0.38268i
          -0.92388 - 0.38268i

> poly(A)
    ans = 1.0000   2.6131   3.4142   2.6131   1.0000

模拟低通滤波器设计

例子

此示例介绍了从给定规格设计模拟低通滤波器的步骤。

规格

CCITT G712 输入滤波器规格的简化版本，只显示低通部分，如侧面的图所示。

通带频率上限为 3 kHz，最大纹波为 0.125 dB。阻带在 4 kHz 时需要衰减 14 dB，在 4.6 kHz 以上需要衰减 32 dB。

滤波器阶数

第一步是评估常用滤波器函数所需的阶数。由于对相位没有要求，因此不需要考虑贝塞尔滤波器。

以下Octave 代码

fs = 40E3;
fPass = 3000;
rPass = 0.125;
fStop1 = 4000;
rStop1 = 14;
fStop2 = 4600;
rStop2 = 32;

order1 = buttord(fPass/(fs/2), fStop1/(fs/2), rPass, rStop1);
order2 = buttord(fPass/(fs/2), fStop2/(fs/2), rPass, rStop2);
buttOrder = max(order1, order2)

order1 = cheb1ord(fPass/(fs/2), fStop1/(fs/2), rPass, rStop1);
order2 = cheb1ord(fPass/(fs/2), fStop2/(fs/2), rPass, rStop2);
cheb1Order = max(order1, order2)

order1 = cheb2ord(fPass/(fs/2), fStop1/(fs/2), rPass, rStop1);
order2 = cheb2ord(fPass/(fs/2), fStop2/(fs/2), rPass, rStop2);
cheb2Order = max(order1, order2)

order1 = ellipord(fPass/(fs/2), fStop1/(fs/2), rPass, rStop1);
order2 = ellipord(fPass/(fs/2), fStop2/(fs/2), rPass, rStop2);
ellipticOrder = max(order1, order2)

disp('Required filter orders:');
printf("  Butterworth      : %2i\n", buttOrder)
printf("  Chebyshev type 1 : %2i\n", cheb1Order)
printf("  Chebyshev type 2 : %2i\n", cheb2Order)
printf("  Elliptic (Cauer) : %2i\n", ellipticOrder)

给出了结果

Required filter orders:
  Butterworth      : 13
  Chebyshev type 1 :  6
  Chebyshev type 2 :  6
  Elliptic (Cauer) :  4

巴特沃斯滤波器所需的硬件量大约是切比雪夫类型 1 的两倍。切比雪夫类型 2 和椭圆滤波器具有切比雪夫类型 1 滤波器没有的零点，因为它是一个全极点函数。因此，它们所需的硬件量也比切比雪夫类型 1 更多。

切比雪夫类型 1 将是为该滤波器选择的候选者。

传递函数

Octave 自动执行频率变换。幅频响应使用

pointNb = 100;
wLog = logspace(2, 5, pointNb);
AdbMin = 40;

[order, wc] = cheb1ord(fPass/(fs/2), fStop2/(fs/2), rPass, rStop2);
order = order + 1;
wc = 1.03 * wc;
[num, den] = cheby1(order, rPass, (fs/2)*wc, 's');
while ( length(num) < length(den) )
  num = [0, num];
endwhile;
Adb = 20*log10(abs(freqs(num, den, wLog)));
Adb(Adb < -AdbMin) = -AdbMin;

figure(1);
semilogx(wLog, Adb);
grid;
hold on;
semilogx([wLog(1), fPass, fPass], -[rPass, rPass, AdbMin], 'r');
semilogx([fStop1, fStop1, fStop2, fStop2, wLog(length(wLog))], ...
        -[0     , rStop1, rStop1, rStop2, rStop2            ], 'r');
hold off;
xlabel('frequency [Hz]');
ylabel('amplitude [dB]');

获得，如下面的图所示

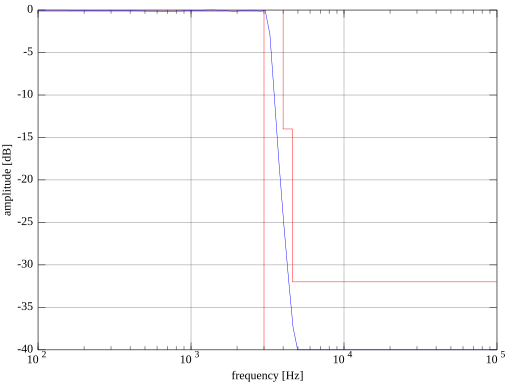
可能已经注意到，滤波器阶数已提升至 7，截止频率也略微提高，以便在通带和阻带侧平衡与规格边界的距离。

滤波器系数

显然，滤波器系数取决于所选的滤波器结构。

对于二阶段串联，高阶传递函数必须分解为二阶传递函数的乘积

[zeroes, poles, gain] = cheby1(order, rPass, (fs/2)*wc, 's');
[SOS, G] = zp2sos(zeroes, poles, gain)

这将得到

SOS = 1.0000e+00   0.0000e+00   0.0000e+00   1.0000e+00   2.0033e+03   3.0335e+06
      1.0000e+00   0.0000e+00   0.0000e+00   1.0000e+00   1.3863e+03   7.0724e+06
      1.0000e+00   0.0000e+00   0.0000e+00   1.0000e+00   4.9478e+02   1.0311e+07
      1.0000e+00   0.0000e+00   0.0000e+00   1.0000e+00   1.1118e+03  -0.0000e+00

G =  2.4594e+23 - 1.3998e+07i

SOS 矩阵行开头的“1, 0, 0”表明它们都是全极点函数。

最后一行 SOS 矩阵，其第三位和最后一位的值为 0，表明它对应于一个一阶段。事实上，7 阶函数由 3 个二阶段和一个一阶段组成。

增益的虚部应该忽略：它肯定是一个定点计算的错误。增益的实部等于 SOS 矩阵行最后一个（非零）元素的乘积。

从这些系数中，可以找到状态变量滤波器或萨伦-基电路的模拟元件值，两者都是全极点型。这些系数也可以几乎按原样在规范双二阶滤波器中使用，但 $b_{1}=0$ 和 $b_{2}=0$ ，简化了电路。