电子学/电感器/网络

串联

考虑如上所示的n个串联电感器。整个装置上的电压（即两个端子上的电压）必须等于各个电感器上的电压之和。

$v_{tot}=v_{1}+v_{2}+\cdots +v_{n}.$

根据我们对电感的定义，电压等于电感乘以电流的变化率，我们得到

$v_{tot}=L_{1}{\frac {di_{1}}{dt}}+L_{2}{\frac {di_{2}}{dt}}+\cdots +L_{n}{\frac {di_{n}}{dt}},$

其中i₁是元件1中的电流，依此类推。由于串联电路中每个元件的电流必须始终相同（根据基尔霍夫电流定律），我们可以看到

$v_{tot}=L_{1}{\frac {di}{dt}}+L_{2}{\frac {di}{dt}}+\cdots +L_{n}{\frac {di}{dt}},$

其中i是网络中的电流。分解后，我们得到

$v_{tot}=\left(L_{1}+L_{2}+\cdots +L_{n}\right){\frac {di}{dt}}$.

如果我们现在将串联中的所有元件称为一个等效电感L_eq，我们会看到

$v_{tot}=L_{eq}{\frac {di}{dt}}.$

因此，

$L_{eq}=L_{1}+L_{2}+\cdots +L_{n}$

这意味着串联时，总电感只是所有组成电感之和。

并联

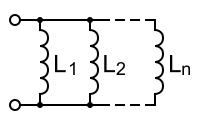
当电感器并联时，每个电感器上的电压相同，即网络端子上存在的电压。这可以简称为v。现在，描述等效电感L_eq的方程式为

$v=L_{eq}{\frac {di_{eq}}{dt}},$

其中i_eq是流经网络的电流。

根据基尔霍夫电流定律，我们有

$i_{eq}=i_{1}+i_{2}+\cdots +i_{n}$

关于时间求导得到

${\frac {di_{eq}}{dt}}={\frac {di_{1}}{dt}}+{\frac {di_{2}}{dt}}+\cdots +{\frac {di_{n}}{dt}}$

现在，通过重新排列描述第i个元件中电感的通用方程式，我们可以为上述每个项获得

${\frac {di_{i}}{dt}}={\frac {v}{L_{i}}}$

代入之前的方程式，我们得到

${\frac {di_{eq}}{dt}}={\frac {v}{L_{1}}}+{\frac {v}{L_{2}}}+\cdots +{\frac {v}{L_{n}}}$

因式分解后，

${\frac {di_{eq}}{dt}}=v\left({\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}\right)$

重新排列，得到

$v={\frac {\frac {di_{eq}}{dt}}{{\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}}}$

$v={\frac {1}{{\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}}}{\frac {di_{eq}}{dt}}$

因此，

$L_{eq}={\frac {1}{{\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}}}$

${\frac {1}{L_{eq}}}={\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}$

这与电阻组合规则相同。