电子学 | 前言 | 基础电子学 | 复杂电子学 | 电学 | 机器 | 电子学史 | 附录 | 编辑
电感器是一种被动的电子元件,其性能取决于频率,用于以磁场形式存储电能。电感器的符号为
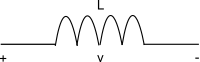
电感是电感器在给定电流下产生磁场的特性。电感用字母 L 表示,单位为亨利(H)。

本节列出了特定情况下的电感公式。请注意,一些公式使用的是英制单位。
自由空间的磁导率 μ0 是一个常数,定义为恰好等于 4π×10-7 H m-1。

- L = 电感 / H
- μr = 磁芯材料的相对磁导率
- N = 匝数
- A = 线圈横截面积 / m2
- l = 线圈长度 / m
![{\displaystyle L_{self}={\frac {\mu _{0}b}{2\pi }}\left[\ln \left({\frac {b}{a}}+{\sqrt {1+{\frac {b^{2}}{a^{2}}}}}\right)-{\sqrt {1+{\frac {a^{2}}{b^{2}}}}}+{\frac {a}{b}}+{\frac {\mu _{r}}{4}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1319287561f2f2913cd9042321f3f29db9db9106)
- Lself = 自感 / H(?)
- b = 导线长度 /m
- a = 导线半径 /m
 = 导线的相对磁导率
= 导线的相对磁导率
如果假设 b >> a 且导线是非磁性的 ( ),则此方程可以近似为
),则此方程可以近似为
![{\displaystyle L_{self}={\frac {\mu _{0}b}{2\pi }}\left[\ln \left({\frac {2b}{a}}\right)-3/4\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c2e4c5b1ece0e0860737ee6415f2983fa3fd9a2) (对于低频)
(对于低频)
![{\displaystyle L_{self}={\frac {\mu _{0}b}{2\pi }}\left[\ln \left({\frac {2b}{a}}\right)-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/051e38457b22f414774e223497e30bd9732f53f7) (由于集肤效应,适用于高频情况)
(由于集肤效应,适用于高频情况)- L = 电感 / H
- b = 线长 / 米
- a = 线径 / 米
直导线的电感通常很小,在大多数实际问题中可以忽略不计。如果问题涉及非常高的频率(f > 20 GHz),则可能需要进行计算。在本手册的其余部分,我们将假设这种自感可以忽略不计。

- L = 电感,单位为μH
- r = 线圈外径,单位为英寸
- l = 线圈长度,单位为英寸
- N = 匝数

- L = 电感,单位为μH
- r = 线圈平均半径,单位为英寸
- l = 线圈绕组的物理长度,单位为英寸
- N = 匝数
- d = 线圈深度,单位为英寸(即外径减去内径)

- L = 电感 / H
- r = 线圈平均半径 / 米
- N = 匝数
- d = 线圈深度 / 米(即外径减去内径)
因此,一个平均半径为 25 毫米、深度为 10 毫米、匝数为 8 匝的螺旋线圈,其电感为 5.13μH。

- L = 电感 / H
- μr = 磁芯材料的相对磁导率
- N = 匝数
- r = 线圈绕组半径 / 米
- D = 环形磁芯的总直径 / 米
选择电感用于电子电路时,需要考虑电感的一些重要特性。以下是一些基本特性。其他类型的电感可能还有一些其他重要的特性,但本文不做介绍。
- 电流承载能力由导线粗细和电阻率决定。
- 品质因数或 Q 值描述了由于制造缺陷导致的电感能量损耗。
- 线圈的电感可能是最重要的,因为它决定了电感的用途。电感是对电流变化的响应。
电感由多个因素决定。
- 线圈形状:矮胖型最佳
- 磁芯材料
- 线圈的匝数。这些匝数必须方向一致,否则会相互抵消,最终得到一个电阻器。
- 线圈直径。直径越大(磁芯面积越大),电感就越大。
对于一个具有以下尺寸的线圈

- 线圈每匝包围的面积为A
- 线圈长度为'l'
- 线圈的匝数为N
- 磁芯的磁导率为μ。μ由真空磁导率μ0乘以相对磁导率μr得到。
- 线圈中的电流为'i'
线圈内部的磁通密度B由下式给出

我们知道,线圈中的磁链λ由下式给出;

因此,

因此,电感中的磁链与电流成正比,假设A、N、l 和μ 都保持不变。比例常数被称为电感(以亨利为单位)并用符号L 表示。

对时间求导,我们得到

由于L 在几乎所有情况下都是时间不变的,我们可以写成

现在,法拉第电磁感应定律指出

我们称 为线圈的电动势(emf),它与电感两端的电压v 相反,得到
为线圈的电动势(emf),它与电感两端的电压v 相反,得到

这意味着电感两端的电压等于电感中电流变化率乘以一个因子,即电感。注意,对于恒定电流,电压为零,而对于瞬时电流变化,电压为无穷大(或更确切地说,未定义)。这仅适用于理想电感,它们在现实世界中并不存在。
这个等式意味着
- 电感两端的电压与通过电感的电流导数成正比。
- 在电感中,电压领先电流。
- 电感对高频有高阻抗,对低频有低阻抗。这种特性使其能够用于过滤信号。
电感的工作原理是通过阻碍电流变化来实现。每当电子加速时,用于“推动”电子的能量中的一部分会转化为电子的动能,但其中大部分能量存储在磁场中。之后,当该电子或其他电子减速(或反向加速)时,能量会从磁场中释放出来。
当一个多匝线圈连接到闭合回路的电源时,电路中的电流会产生磁场,该磁场具有与磁铁磁场相同的特性。

当电流关闭时,磁场不再存在。

导电线圈被称为电磁铁。


 ,其中
,其中  .
.

对于无损电感
- 电压和电流之间的角度差为90
对于有损电感

改变L和RL的值将改变角度差、角频率、频率和时间的值。




品质因数用Q表示,定义为存储的能量与元件中所有能量损耗之和的比率





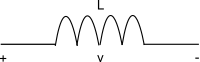


![{\displaystyle L_{self}={\frac {\mu _{0}b}{2\pi }}\left[\ln \left({\frac {b}{a}}+{\sqrt {1+{\frac {b^{2}}{a^{2}}}}}\right)-{\sqrt {1+{\frac {a^{2}}{b^{2}}}}}+{\frac {a}{b}}+{\frac {\mu _{r}}{4}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1319287561f2f2913cd9042321f3f29db9db9106)


![{\displaystyle L_{self}={\frac {\mu _{0}b}{2\pi }}\left[\ln \left({\frac {2b}{a}}\right)-3/4\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c2e4c5b1ece0e0860737ee6415f2983fa3fd9a2)
![{\displaystyle L_{self}={\frac {\mu _{0}b}{2\pi }}\left[\ln \left({\frac {2b}{a}}\right)-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/051e38457b22f414774e223497e30bd9732f53f7)





























