电子学/运算放大器/线性配置

反相运算放大器

反相运算放大器的闭环增益“mon then”为

$R_{1}=R_{in}$

$A_{f}=-{\frac {R_{f}}{R_{1}}}$ (i)

此配置的输入阻抗为 $Z_{in}=R_{in}$ (因为 $V_{-}$ 是虚拟地，理想情况下没有电流流入运算放大器）。

为了得到公式 (i)，我们用 $V_{in}$，$R_{1}$ 和运算放大器的输入构建一个 KVL 循环。这将得到

$V_{in}=i_{in}R_{1}+v_{d}\,$

其中 $v_{d}$ 是 $v_{+}-v_{-}$，即非反相输入和反相输入之间的电压。但对于理想运算放大器，$v_{d}$ 近似为零。$v_{d}$ 为零是因为输入阻抗为无穷大，这意味着通过阻抗的电流必须为零，根据欧姆定律。零电流意味着阻抗上没有压降。这将得到

$i_{in}={\frac {V_{in}}{R_{1}}}$ (5)

使用这个想法。

$i_{f}={\frac {V_{out}}{R_{f}}}$(6)

如果我们在反相输入处进行 KCL，那么

$i_{in}=i_{d}-i_{f}\,$

对于理想运放，由于其输入阻抗无穷大，所以没有输入电流。因此可以使用公式 5 和 6。

$-{\frac {V_{in}}{R_{1}}}={\frac {V_{out}}{R_{f}}}$

因为

$A_{f}={\frac {V_{out}}{V_{in}}}=-{\frac {R_{f}}{R_{1}}}$

---

示例 1

设计一个反向放大器，将 100mV 的信号放大到 1V 的信号。假设：无源阻抗。

解决方案

步骤 1：计算所需的增益。

$|A_{f}|={\frac {1}{0.1}}=10$

步骤 2：选择 $R_{f}$ 的值。

选择 $R_{f}=100k\Omega$.

步骤 3：使用公式 (i) 计算 $R_{1}$ 的所需值。

$R_{1}={\frac {100k}{10}}=10k\Omega$

示例 2

设计一个反向放大器，将 10mV 的信号放大到 1V 的信号。信号具有 100 $\Omega$ 的源阻抗。放大器不能反转信号。

解决方案

由于电压不能反转，因此必须有偶数个级。为了简单起见，我们选择两个级。假设一个理想运放。

步骤 1：计算所需的增益。

$A_{f_{tot}}={\frac {1}{0.01}}=100$

步骤 2：选择每个级所需的增益。

两级的增益都将为 10。但在第一级，我们必须考虑负载的影响。

步骤 3：选择输入阻抗的值，即选择 $R_{1}$.

选择 $10k\Omega$。现在我们可以通过分压器计算运放的输入电压。

$V_{in}={\frac {R_{1}V_{s}}{R_{1}+R_{s}}}={\frac {(10k)(10mV)}{10k+100}}=9.9mV$

我们希望这一级的输出为 100mV。

$A_{f1}={\frac {100}{9.9}}=10.1$

步骤 4：使用 $A_{f1}$ 计算 $R_{f1}$.

使用公式 (i) $R_{f}=A_{f1}R_{1}=101k\Omega$

步骤 5：为第二级选择一个 $R_{f}$。

选择 100k。

步骤 6：使用公式 (i) 计算 $R_{1}$。

$R_{1}=10k\Omega$

---

非反相运算放大器

一个以非反相放大器配置连接的运算放大器

非反相运算放大器的闭环增益为

$A_{f}=1+{\frac {R_{2}}{R_{1}}}$ (ii)

这种配置的输入阻抗为 Zin = ∞（实际上，运算放大器本身的输入阻抗为 1 MΩ 至 10T Ω）。

理想运算放大器推导

对运算放大器和 R₁ 的输入进行 KVL 分析。

$V_{in}=v_{d}+V_{R1}\,$

但 $v_{d}$ 为零，因为运算放大器是理想的。因此

$V_{in}=V_{R1}\,$(3)

根据分压器规则

$V_{R1}={\frac {V_{out}R_{1}}{R_{1}+R_{2}}}$(4)

将公式 4 代入 3。

$V_{in}={\frac {V_{out}R_{1}}{R_{1}+R_{2}}}$

因此

$A_{f}={\frac {V_{out}}{V_{in}}}=1+{\frac {R_{2}}{R_{1}}}$

反馈分析推导

如果输出连接到反相输入，在通过一个分压器 K = R₁ / (R₁ + R₂) 进行缩放后，那么

V₊ = V_in

V₋ = K V_out

V_out = G(V_in − K V_out)

求解 V_out / V_in，我们可以看到结果是一个增益为

V_out / V_in = G / (1 + G K)

如果 G 很大，V_out / V_in 将接近 1 / K，等于 1 + (R2 / R1)。

这种负反馈连接是运算放大器最典型的用法，但还有许多不同的配置方式，使其成为所有电子构建模块中最通用的之一。

当以负反馈配置连接时，运算放大器将倾向于输出使输入电压相等的任何电压。这以及高输入阻抗有时被称为运算放大器设计的两条“黄金法则”（用于使用反馈的电路）

1. 没有电流流入输入端
2. 输入电压彼此相等

唯一的例外是如果所需的电压大于运算放大器的电源电压，在这种情况下，输出信号将停止在电源轨附近，V_S+ 或 V_S−。

---

示例 3

设计一个非反相放大器，将 100mV 信号放大为 1V 信号。假设：没有源阻抗。

步骤 1：计算所需的增益。

$A_{f}={\frac {1}{0.1}}=10$

步骤 2：选择一个 $R_{2}$ 值。

选择$R_{2}=90k\Omega$。

步骤 3：使用方程式 (ii) 计算出所需的$R_{1}$ 值。

$10=1+{\frac {90k}{R_{1}}}$

$R_{1}={\frac {90k}{9}}=10k\Omega$

---

示例 4（快速设计步骤）

我想要放大增益为 8 的信号 A。我们想要至少 -3 到 +3 V 的输出摆幅。

我们有一个 5V 和 -5V 的电源可用，所以我们可以使用它。

1. 信号 A 的增益为 8。

2. 地增益 = 1 - (8) = -7。

3. 反馈电阻值：Rf = 100 千欧。

4. 每个输入的电阻值

• R_A = 100 kΩ / 8 = 12.5 kΩ
• R_地 = 100 kΩ / |-7| = 14.3 kΩ

由于信号 A 的增益为正，将其电阻连接到 V₊。由于地增益为负，将其电阻连接到 V₋。

---

示例 5

设计一个两级非反相放大器，将 10mV 信号放大到 1V 信号。信号的源阻抗为 100 Ω。

解决方案 假设一个理想运算放大器。由于该配置具有运算放大器本身的输入阻抗。我们不必担心加载，因为输入阻抗是无限的。

步骤 1：计算所需的增益。

$A_{f}={\frac {1}{0.01}}=100$

步骤 2：选择每个级的增益。

对两个级都选择 10。

步骤 3：选择$R_{2}$ 电阻在两个级中的值。

对两个级都选择 90kΩ。

步骤 4：计算出$R_{1}$ 的值。

使用方程式 (ii) $R_{1}=10k\Omega$。

---

电压跟随器

电压跟随器

此配置也被称为单位增益缓冲器。因为它可以用来抵消源加载的影响。它提供的输入阻抗甚至高于普通的非反相放大器，因为增益降低了该输入阻抗。增益由方程式 (ii) 给出。但 R_2 短路，R_1 开路。

$A_{f}=1+{\frac {R_{2}}{R_{1}}}=1+{\frac {0}{\infty }}=1$

差分放大器

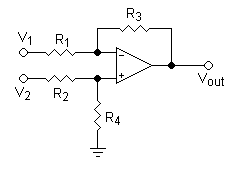
差分放大器

此配置只是同时连接的反相和非反相配置。电阻 R₂ 和 R₄ 是一个分压器。考虑 R₄ 开路，R₂ 短路的情况。现在，从方程式 (i) 和 (ii) 我们知道，V₁ 的增益是

$A_{f1}=-{\frac {R_{3}}{R_{1}}}$

而 V₂ 的增益是

$A_{f2}=1+{\frac {R_{3}}{R_{1}}}$

现在如果我们将 $A_{f1}$ 设置为 -10，那么 $A_{f2}$ 将变为 11。这意味着 V_out 将是

$V_{out}=V_{1}A_{f1}+V_{2}A_{f2}=V_{2}(11)-(10)V_{1}$

这意味着如果 $V_{1}=V_{2}$，那么 V_out 将是 V₂。这对大多数情况来说没什么用，因为数学上我们希望答案为零。但是，如果我们使非反相输入的电压等于 10/11，那么当电压相等时，我们将得到零。

当 R₄ 和 R₂ 连接时，V₂ 的增益为

$A_{f2}={\frac {(1+{\frac {R_{3}}{R_{1}}})R_{4}}{R_{4}+R_{2}}}$ (x)

V₁ 的增益为

$A_{f1}=-{\frac {R_{3}}{R_{1}}}$ (y)

如果我们想要 $A_{f2}=|A_{f1}|$

${\frac {R_{3}}{R_{1}}}={\frac {(R_{1}+R_{3})R_{4}}{(R_{4}+R_{2})R_{1}}}$

我们只需设置 $R_{4}=R_{3}$ 和 $R_{2}=R_{1}$.

这种配置具有较低的输入阻抗。V₁ 看到的输入阻抗是 R₁，就像反相放大器中一样。V₂ 看到的输入阻抗是 R₂ + R₄。

---

示例 6（快速设计步骤）

我们通常希望将一个信号 A 从另一个信号 B 中减去，并将差值放大 10 倍。我们希望输出摆幅至少为 -6V 到 +6V。另外，出于安全考虑，A 和 B 每个都有 8 kΩ 的源阻抗。

我们的 5V 和 -5V 电源供应不足，因此我们选择 +12V 和 -12V 电源供应。

1.

• B 的增益为 +10。
• A 的增益为 -10。

2. 地增益 = 1 - (+10 + -10) = +1。

3. 反馈电阻值：Rf = 100 千欧。

4. 每个输入的电阻值

• R_A = 100 kΩ / |-10| = 10 kΩ
• R_B = 100 kΩ / |+10| = 10 kΩ
• R_ground = 100 kΩ / |+1| = 100 kΩ

因此，我们将 100 kΩ 的 Rf 从 V_out 连接到 V₋，另一个 100 kΩ 从地连接到 V₊。然后我们将 2 kΩ 从 R_A 连接到 V₋，另一个 2 kΩ 从 R_B 连接到 V₊。

如果输入具有源阻抗，则源阻抗是电路的一部分。8 kΩ 的源阻抗加上我们添加的 2 kΩ 物理电阻，使我们得到理想电压源和运算放大器输入之间的总阻抗为 10 kΩ。

---

反相求和放大器

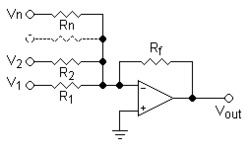
反相求和放大器

这仅仅是一个具有额外输入的反相放大器。分析几乎相同，但我们有许多电流等于反馈电流。如果我们在反相输入处进行 KCL。

$i_{n}+\cdots +i_{2}+i_{1}=-i_{f}$

电流值可以通过欧姆定律确定，使用理想运算放大器的 v_d 为零的事实。

${\frac {V_{n}}{R_{n}}}+\cdots +{\frac {V_{2}}{R_{2}}}+{\frac {V_{1}}{R_{1}}}=-{\frac {V_{out}}{R_{f}}}$

如果 $R_{n}=\cdots =R_{2}=R_{1}$ 那么

${\frac {1}{R_{1}}}(V_{n}+\cdots +V_{2}+V_{1})=-{\frac {V_{out}}{R_{f}}}$

$A_{f}=-{\frac {V_{out}}{V_{sum}}}=-{\frac {R_{f}}{R_{1}}}$

就像反向放大器一样。

注意：还有一种使用同向放大器配置的求和放大器。该配置稍微复杂一些，难以使用，因为它需要理解叠加原理。

理想积分器

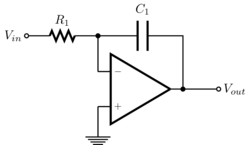
积分放大器

该配置是一个反向放大器，其反馈电阻是一个电容。推导过程相同。

$i=-i_{f}$

${\frac {V_{in}}{R}}=-C{\frac {\;dV_{out}}{\;dt}}$

${\frac {V_{in}}{RC}}=-{\frac {\;dV_{out}}{\;dt}}$

将两边关于

$V_{out}=\int _{t_{0}}^{0}-{\frac {V_{in}}{RC}}\,dt+V_{initial}$

实际上，一个电阻通常与反馈电容并联。这意味着在非常低的频率下没有无限增益，这使得实际积分器更加稳定。

理想微分器

该配置是一个反向放大器，其电容作为第一个电阻，因此推导过程与之前相同。

$i=-i_{f}\,$

$C{\frac {\;dV_{in}}{\;dt}}=-{\frac {V_{out}}{R}}$

$V_{out}=-RC{\frac {\;dV_{in}}{\;dt}}$

这种配置由于几个原因不稳定。较高频率的输入将具有更高的导数。这意味着电路充当低通滤波器，但更重要的是，这意味着如果将高频信号输入到微分器，它将直接饱和。这也是通过增益看到的。

$A_{f}=-{\frac {R}{1/j\omega C}}$

这意味着高频意味着高增益，从而导致饱和。

在实际应用中，电阻器通常与电容器串联连接。