电子学/运算放大器

电子学 | 前言 | 基础电子学 | 复杂电子学 | 电学 | 机器 | 电子学史 | 附录 | 编辑

运算放大器 (operational amplifier)

运算放大器，简称运放，是一种集成电路(IC)芯片。它是一个电子电路，包含许多电子元件，它们已经连接并封装在芯片内部，并提供多个引脚用于外部连接。最初，运算放大器之所以得名，是因为它们被用于电子模拟计算机中，来模拟加法、减法、积分、微分等基本数学运算。从这个意义上说，真正的运算放大器是一个理想的电路元件。

运算放大器	引脚	符号

741 运算放大器

符号

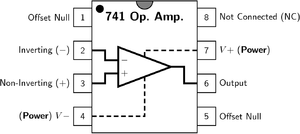
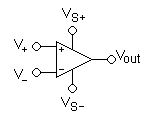
741 运算放大器具有如图所示的符号。

其引脚为

V₊: 非反相输入
V₋: 反相输入
V_out: 输出
V_S+: 正电源
V_S−: 负电源

运作

741 运算放大器可以被认为是通用电压差放大器。741 运算放大器的主要功能是放大两个输入电压的差值，可以用以下数学表达式表示

V_{o}=A(V_{+}-V_{-})

从

V_{o}=A(V_{+}-V_{-})

. 运算放大器起着电压差放大器的作用。

可以证明，运算放大器可以作为非反相电压放大器或反相电压放大器。

V_{o}=AV_{+}

.

V_{-}=0

. 运算放大器作为非反相电压放大器。

V_{o}=-AV_{-}

.

V_{+}=0

. 运算放大器作为反相电压放大器。

此外，可以证明，运算放大器可以作为电压比较器。

V_{o}=0

.

V_{-}=V_{+}

. 两个输入电压之间没有差异

V_o = V_S+ .

V_{+}>V_{-}

. 非反相输入电压大于反相输入电压

V_o = V_S- .

V_{-}>V_{+}

. 反相输入电压大于非反相输入电压。

理想运算放大器

输出电压是正负输入之差乘以开环增益。

V_out = (V₊ − V₋) * A_vo.

理想运算放大器具有

无限开环增益，

无限输入阻抗和

零输出阻抗。

输入阻抗是指非反相输入和反相输入之间的阻抗。

运算放大器的模型如图 1 所示。其中 V₊ − V₋ 等于 v_d；R_in 是输入阻抗；R_out 是输出阻抗；A_vo 是开环增益；R_s 是源阻抗。

图 1：运算放大器的模型。

使用分压器规则，我们可以确定电压 v_d。

v_{d}={\frac {V_{in}R_{in}}{R_{in}+R_{s}}}

(1)

由于受控电压源将电压 v_d 放大 A_vo 倍。我们再次使用分压器规则可以算出 R_L 两端的输出电压。

V_{out}={\frac {A_{vo}v_{d}R_{L}}{R_{L}+R_{out}}}

(2)

将公式 1 代入公式 2。

V_{out}={\frac {A_{vo}V_{in}R_{in}R_{L}}{(R_{L}+R_{out})(R_{in}+R_{s})}}

现在如果应用理想运算放大器的特性。理想运算放大器的特性是无限的输入阻抗和零输出阻抗。由于 R_in >>，远大于 R_s，R_in/(R_in+R_s) $\approx$ 1。

V_{out}=A_{vo}V_{in}\,

这基本上是运算放大器的定义。但是如果输入阻抗不是无限的，输出阻抗也不是零，那么就不是这样。

实际运算放大器

实际运算放大器通常是以集成电路的形式制造的，但有时也使用分立晶体管或真空管。实际运算放大器是理想运算放大器的近似值。实际运算放大器没有无限的开环增益、无限的输入阻抗或零输出阻抗。实际运算放大器还会在电路中产生噪声，并具有偏移电压、热漂移和有限带宽。

偏移电压

意味着当两个输入都接地时，存在一个电压 v_d。这种偏移称为输入偏移，因为电压 v_d 偏离了其理想值零伏。输入偏移电压乘以开环增益，得到输出偏移电压。

热漂移

意味着运算放大器的特性随温度变化而变化。也就是说，开环增益、输入和输出阻抗、偏移电压和带宽都会随着温度的变化而变化。

有限带宽

运算放大器是由晶体管组成的。晶体管由于其自身的某些电容，只能以一定速率响应。这意味着运算放大器无法对高于一定水平的频率做出足够快的响应。这个水平就是带宽。

现代集成电路 MOSFET 运算放大器在有限带宽、大信号应用中，在室温下越来越接近这些理想值。当近似值足够接近时，我们就可以继续将实际器件称为“运算放大器”，忽略其限制，并使用本文中给出的思想和公式。

直流特性

开环增益定义为从输入到输出的放大倍数，没有任何反馈。在大多数实际计算中，开环增益被认为是无限的；然而在现实中，它受限于为运算放大器供电的电压量，即上图中的 Vs+ 和 Vs-。典型器件的开环直流增益在 100,000 到 100 万以上之间。这使得使用负反馈可以轻松、准确地设置应用中的增益。当然，理论和实践会有所不同，因为运算放大器存在设计者必须牢记并有时需要克服的限制。

交流特性

在直流条件下计算的运算放大器增益在较高频率下不适用。这种现象是由于运算放大器本身的限制（如有限带宽）以及运算放大器所处电路的交流特性造成的。在使用运算放大器进行设计时，最著名的障碍是器件在高频下发生谐振的趋势，因为寄生低通滤波器会使负反馈变为正反馈。

典型的低成本通用运算放大器的增益带宽积为几兆赫兹。专用高速运算放大器的增益带宽积可以达到几百兆赫兹。

运算放大器配置

应用

快速设计流程

假设我们有一个（弱）输入信号，我们想放大它以产生一个强大的输出信号；或者我们有几个不同的电压，我们想将它们加在一起。为了实现这些目的，我们需要运算放大器放大和求和电路。这些基本的（通常是单运算放大器）电路似乎没有新东西可以说了。只是创新者 Dieter Knollman 在一篇 EDN 文章 ^[1] 中提出了一种新的更简单的设计方法。他还将他的工作发布在网上^[2]（参见在 Dieter 工作之后写的一篇电路故事^[3]）。

我们假设

所有输入都是理想电压源。
增益定义为从理想电压源到运算放大器输出的增益。
反馈电阻 Rf 连接从运算放大器输出到反相输入。
输入电阻 Ri 连接从理想电压源输入到运算放大器输入。（这 *包含* 任何源电阻）。
- 正增益输入通过该电阻连接到 V₊
- 负增益输入通过该电阻连接到 V₋

设计步骤

首先，指定每个输入所需的电路增益。
然后计算地增益，如下所示

黛西定理

在一个设计合理的运算放大器电路中，增益之和 = +1。

因此，选择

地增益 = 1 - (所需的正增益和负增益之和).

选择一个反馈电阻值。例如，设 Rf=100 千欧。

接下来，使用以下公式计算每个输入的电阻值，包括地增益电阻。

Ri={\frac {Rf}{|gain|}}

.

其中 |gain| 是所需增益的绝对值。

一些运算放大器电路需要从运算放大器的反相输入到地连接一个电阻。其他电路需要在同相输入上连接一个到地的电阻。地增益的符号决定了将地电阻放置在何处。

如果所需的增益之和为 1，则无需连接到地的电阻。

您将在下面看到一些示例，说明如何使用快速设计步骤。首先，回答这个问题，“您希望输出电压的最高和最低值是多少？”确保运算放大器的电源端至少达到这些最高和最低值。（如果您希望它从 +5 V 摆动到 -5 V，那么连接到 0 V 和 +10 V 的运算放大器将无法工作）。

通用运算放大器有两个输入和一个输出。（有些是用浮动、差分输出制作的。）输出电压是两个输入之差的倍数。

浮动输出？您可能误解了“全差分放大器” ？

V_out = G(V₊ − V₋)

G 是运算放大器的开环增益。假定输入具有非常高的阻抗；输入不会流入或流出明显的电流。运算放大器输出具有非常低的源阻抗。

如果运算放大器与正反馈一起使用，它可以充当振荡器。

其他符号

电源引脚（V_S+ 和 V_S−）可以用多种不同的方式标记。对于基于 FET 的运算放大器，正极公共漏极电源标记为 V_DD，负极公共源极电源标记为 V_SS。对于基于 BJT 的运算放大器，V_S+ 引脚变为 V_CC，V_S− 变为 V_EE。它们有时也标记为 V_CC+ 和 V_CC−，甚至 V₊ 和 V₋，在这种情况下，输入将被不同地标记。功能保持不变。