理论

维基百科^[1]
数学论坛：阿波罗尼奥斯问题 ^[2]

如何计算和绘制阿波罗尼奥斯垫片？

符号

阿波罗尼奥斯垫片 = 曲线型谢尔宾斯基垫片 = 莱布尼茨填充 = 阿波罗尼奥斯填充
阶段 = 层级 = 步
内切圆 = 内接圆 = 3 个圆内的圆 = 内圆
间隙 = 曲线型三角形 = 理想三角形（因为边在每个顶点处相切，它们之间的角度为零）= 3 个相切圆之间的区域

算法

阿波罗尼奥斯垫片可以使用以下算法制作：^[3]

曼德尔布罗特算法 ^[4]（使用圆反演）^[5]^[6]
索迪算法（使用圆的笛卡尔定理）^[7]^[8]
阿列克谢·克拉夫琴科和德米特里·梅洪特塞夫的 IFS 算法 ^[9]

所有算法在 n 个阶段后给出状态。它是一个无限多个阶段（圆圈）的极限集的近似值。

曼德尔布罗特算法

（待办事项）

索迪算法

它将通过具有初始配置的示例垫片进行解释：3 个具有整数曲率的内圆

(k_{ia},k_{ib},k_{ic})=(32,32,33)

该算法使用

由中心 $c_{n}$ 和曲率 $k_{n}$ 定义的先前圆
圆的笛卡尔定理来计算下一个圆的曲率 $k_{4}$

k_{4}=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}}}

复圆的笛卡尔定理来计算下一个圆的中心 $c_{4}$

c_{4}={\frac {c_{1}k_{1}+c_{2}k_{2}+c_{3}k_{3}\pm 2{\sqrt {k_{1}k_{2}c_{1}c_{2}+k_{2}k_{3}c_{2}c_{3}+k_{1}k_{3}c_{1}c_{3}}}}{k_{4}}}

当外圆圆心位于原点时，需要在圆心情况下选择解。当整个垫片位于笛卡尔平面第一象限时，更容易。然后所有圆心都有正部分（实部和虚部）。

函数

用于计算曲率和圆心的函数

f_{p}(a_{1},a_{2},a_{3}){\overset {\underset {\mathrm {def} }{}}{=}}a_{1}+a_{2}+a_{3}+2\cdot {\sqrt {a_{1}a_{2}+a_{2}a_{3}+a_{3}a_{1}}}

f_{\color {Red}m}(a_{1},a_{2},a_{3}){\overset {\underset {\mathrm {def} }{}}{=}}a_{1}+a_{2}+a_{3}{\color {Red}-}2\cdot {\sqrt {a_{1}a_{2}+a_{2}a_{3}+a_{3}a_{1}}}

注意，变量 $a_{i}$ 可以是曲率 $k_{i}$ 或 $c_{i}*k_{i}$ 因此 $f_{p}$ 可用于计算曲率和圆心

用于计算 ck 列表的函数

使用列表 $ck$ 更容易定义圆。它包含两个元素：圆心 $c$ 和曲率 $k$

$ck=[c,k]$

$c=ck[1]$

$k=ck[2]$

现在可以定义新的函数（Maxima CAS 代码）来计算与给定的 3 个圆相切的第 4 个圆。

f_pp(ck1,ck2,ck3):=block
([c4,k4,ck4],
k4:f_p(ck1[2],ck2[2],ck3[2]),
c4:f_p(ck1[1]*ck1[2],ck2[1]*ck2[2],ck3[1]*ck3[2])/k4,
ck4:[c4,k4])$

f_pm(ck1,ck2,ck3):=block
([c4,k4,ck4],
 k4:f_p(ck1[2],ck2[2],ck3[2]),
 c4:f_m(ck1[1]*ck1[2],ck2[1]*ck2[2],ck3[1]*ck3[2])/k4,
 ck4:[c4,k4]);

f_mm(ck1,ck2,ck3):=block
([c4,k4,ck4],
 k4:f_m(ck1[2],ck2[2],ck3[2]),
 c4:f_m(ck1[1]*ck1[2],ck2[1]*ck2[2],ck3[1]*ck3[2])/k4,
 ck4:[c4,k4]);

 f_mp_ck4(ck1,ck2,ck3):=block
([c4,k4],
k4:solve_m_eq(ck1[2],ck2[2],ck3[2]),
c4:solve_p_eq(ck1[1]*ck1[2],ck2[1]*ck2[2],ck3[1]*ck3[2])/k4,
return([c4,k4])
);

函数 $f_{pp}$ 使用 $f_{p}$ 函数来计算圆心和曲率。它用于计算几乎所有没有外圆的圆和硬圆。

函数 $f_{pm}$ 使用 $f_{p}$ 函数来计算曲率和 $f_{m}$ 函数来计算圆心。它用于计算硬圆。

函数 $f_{mm}$ 使用 $f_{m}$ 函数来计算圆心和曲率。它用于计算外圆。

用于填充间隙的函数

fill_easy(ckla,cklb,cklc,max_stage):=block
([ckm],
 if max_step>0 then (
  /* circle in the middle */
  ckm:give_pp_ck4(ckla,cklb,cklc),
  /* 3 circles around */
  fill_easy(ckla,cklb,ckm,max_stage-1),
  fill_easy(cklb,cklc,ckm,max_stage-1),
  fill_easy(ckla,cklc,ckm,max_stage-1)))$

fill_hard(ck_ic,ck_ia,ck_0out,max_stage):=block
([ck_1c,ck_2cc,ck_3ccc,ck_4ccca,ck_5cccac], /* hard circles */
 if 	max_stage>0 then (
  /* step 1 = circle in the middle */
  ck_1c:f_pm(ck_ia,ck_ic,ck_0out),      /* 1c */
  /* step 2 = 3 circles around */
  fill_easy(ck_ia,ck_0out,ck_1c,max_stage-1), /* 2ca */
  fill_easy(ck_ia,ck_ic,ck_1c,max_stage-1), /* 2cb */
  /* hard subgap 2cc */
  if max_stage>1 then ck_2cc:f_pm(ck_ic,ck_1c,ck_0out), /* 2cc */
  /* step 3 for subgap 2cc */
  fill_easy(ck_0out,ck_1c,ck_2cc,max_stage-2), /* 3cca */
  fill_easy(ck_ic,ck_1c,ck_2cc,max_stage-2),  /* 3ccb */
  if max_stage>2 then ck_3ccc:f_pm(ck_ic,ck_0out,ck_2cc),	/* 3ccc */
  /* step 4 for subgap 3ccc */
  if max_stage>3 then ck_4ccca:f_pm(ck_0out,ck_2cc,ck_3ccc),
  fill_easy(ck_ic,ck_2cc,ck_3ccc,max_stage-3),  /* 4cccb */
  fill_easy(ck_ic,ck_0out,ck_3ccc,max_stage-3),  /* 4cccc */
  /* step 5 for subgap 4ccca */
  fill_easy(ck_0out,ck_2cc,ck_4ccca,max_stage-4),  /*  5cccaa */
  fill_easy(ck_2cc,ck_3ccc,ck_4ccca,max_stage-4),  /* 5cccab */
  if max_stage>4 then ck_5cccac:f_pm(ck_0out,ck_3ccc,ck_4ccca)))$

构造

初始阶段：3 个相互相切的圆 = $(k_{ia},k_{ib},k_{ic})$
零阶段：2 个与前一个圆相切的圆：外圆 $ck_{0out}$ 和内圆 $ck_{0in}$ ，其中：

{\color {Red}ck}_{0out}=f_{\color {Red}mm}(ck_{ia},ck_{ib},ck_{ic})

ck_{0in}=f_{pp}(ck_{ia},ck_{ib},ck_{ic})

第一阶段：在之前的圆之间有 6 个空隙（= 曲线三角形）。三个空隙在圆周上（靠近外圆），三个空隙在中间（靠近内圆）。在每个空隙中放一个圆。

ck_{1a}=f_{pp}(ck_{ia},ck_{ib},ck_{0out})

ck_{1b}=f_{pp}(ck_{ib},ck_{ic},ck_{0out})

{\color {Red}c}k_{1c}=f_{p{\color {Red}m}}(ck_{ic},ck_{ia},ck_{0out})

ck_{1d}=f_{pp}(ck_{ia},ck_{ib},ck_{0in})

ck_{1e}=f_{pp}(ck_{ib},ck_{ic},ck_{0in})

ck_{1f}=f_{pp}(ck_{ic},ck_{ia},ck_{0in})

每个放在空隙中的新圆都会形成三个新的空隙（三叉）。

第二阶段：有 18（6*3）个新的空隙。使用 $f_{pp}$ 函数在每个空隙中放置一个圆，除了一个硬圆。

{\color {Red}c}k_{2cc}:f_{p{\color {Red}m}}(ck_{ic},ck_{1c},ck_{0out})

后续阶段：在每个阶段的每个空隙中放置一个圆。在每个阶段，只有一个硬圆，它在 $1c$ 空隙中。

程序员算法

由于所有圆都内切于外圆，因此从外圆开始更容易。

选择二次图像的大小 $side$
计算外圆的半径

r_{0out}={\frac {side}{2}}

将外圆放置在笛卡尔平面的第一象限

c_{0out}=r_{0out}+r_{0out}*i

计算 3 个相等的初始圆的半径^[10]

a=1+{\frac {2}{\sqrt {3}}}

r_{i}={\frac {r_{0out}}{a}}

找到初始圆的圆心。例如，将一个圆 $ia$ 放在上排，两个圆 ( $ib$ 和 $ic$ ) 放在下排。

然后这些圆的圆心是等边三角形的顶点，三角形边长 $=2*r_{i}$ 因此

$height=r_{i}*{\sqrt {3}}$

$c_{ia}=r_{0out}+(2*r_{0}out-r_{i})*i$

$c_{ib}=(r_{0out}+r_{i})+(2*r_{0}out-r_{i}-height)*i$

$c_{ic}=(r_{0out}-r_{i})+(2*r_{0}out-r_{i}-height)*i$

计算内圆 $0in$

ck_{0in}=f_{pp}(ck_{ia},ck_{ib},ck_{ic})

"现在我们有一个可以开始的配置"^[11] 有 6 个空隙要填补。5 个空隙很容易填补，而一个空隙 $1c$ 很难填补。

圆之间的关系

{\color {Red}ck}_{0out}=f_{\color {Red}mm}(ck_{ia},ck_{ib},ck_{ic})

ck_{0in}=f_{pp}(ck_{ia},ck_{ib},ck_{ic})

{\color {Red}ck}_{ia}=f_{\color {Red}mm}(ck_{ib},ck_{ib},ck_{0out})

c{\color {Red}k}_{ib}=f_{{\color {Red}m}p}(ck_{ia},ck_{ic},ck_{0out})

{\color {Red}ck}_{ic}=f_{\color {Red}mm}(ck_{ia},ck_{ib},ck_{0out})

圆圈数量

第 n 阶段新圆圈数量 = $2*3^{n}$
n 阶段后圆圈总数 = $2+3^{n+1}$

其中 $n>=0$

例如

阶段 -1 = 初始配置（3 个内圆）
阶段 0 给出 2 个新圆（一个外圆和一个最内圆）。所有圆圈 = 5
阶段 1 给出 6 个新圆（所有圆圈 = 11）
阶段 2 给出 18 个新圆（所有圆圈 = 29）
阶段 3 给出 54 个新圆（所有圆圈 = 83）
阶段 4 给出 162 个新圆（所有圆圈 = 245）
阶段 5 给出 486 个新圆（所有圆圈 = 731）
阶段 6 给出 1 458 个新圆（所有圆圈 = 2 189）
阶段 7 给出 4 374 个新圆（所有圆圈 = 6 563）
阶段 8 给出 13 122 个新圆（所有圆圈 = 19 685）
阶段 9 给出 39 366 个新圆（所有圆圈 = 59 051）
阶段 10 给出 118 098 个新圆（所有圆圈 = 177 149）
阶段 11 给出 354 294 个新圆（所有圆圈 = 531 443）
阶段 12 给出 1 062 882 个新圆（所有圆圈 = 1 594 325）
阶段 13 给出 3 188 646 个新圆（所有圆圈 = 4 782 971）
阶段 14 给出 9 565 938 个新圆（所有圆圈 = 14 348 909）
阶段 15 给出 28 697 814 个新圆（所有圆圈 = 43 046 723）
阶段 16 给出 86 093 442 个新圆（所有圆圈 = 129 140 165）
阶段 17 给出 258 280 326 个新圆（所有圆圈 = 387 420 491）
阶段 18 给出 774 840 978 个新圆（所有圆圈 = 1 162 261 469）
阶段 19 给出 2 324 522 934 个新圆（所有圆圈 = 3 486 784 403）
阶段 20 给出 6 973 568 802 个新圆（所有圆圈 = 10 460 353 205）

可以使用 Maxima CAS 代码计算

 NumberOfStageCircles(stage):= 
  if stage =-1 then 3
  elseif stage=0 then 2
  else 2*3^stage;

 NumberOfAllCircles(stage_max):=sum(NumberOfStageCircles(i),i,-1,stage_max);

for i:-1 step 1 thru 20 do print("stage ",i," gives ",NumberOfStageCircles(i)," new circles ( all circles =  ",NumberOfAllCircles(i), " )");

圆圈数量快速增长，导致大文件尺寸问题。可以

仅使用最多 5-7 阶段。这似乎足以在短时间内生成良好的图像。^[12]
不要绘制太小的圆圈（半径小于像素尺寸）^[13]
将 svg 文件转换为 png（例如使用 Image Magic : "convert a.svg a.png"）。然后，阶段 12 svg 图像为 128 MB，而 png 文件仅为 57 KB。
高兴的是你得到了如此详细的图像，并等待很长时间加载文件，或者看看系统如何挂起（:-））

曲率

注意，只有一个曲率是用 $f_{\color {Red}m}$ 函数计算的。

它是 $k_{0out}$ 。它也是唯一的负曲率。

所有其他曲率都是用 $f_{p}$ 函数计算的。

阶段 $n\,$	曲率
-1	$(32,32,33)\,$
0	$({\color {Red}-15},209)\,$
1	$(68,65,68,516,513,516)\,$
2	$(953,1481,1484,945,1476,1476,953,1484,1481,281,137,140,273,132,132,68,137,140)\,$

示例程序

Haskell 和 EDSL Diagrams

图像和代码来自 Brent Yorgey^[14]
diagrams 代码^[15]

Java

Ken Stephenson 编写的 CirclePack 程序

Maxima CAS

程序在上面解释过，源代码在 Apollonian_rc_6.svg 的描述中。

Common Lisp

要运行，请将 apollonian.lisp 文件放到您的主目录和 Emacs/slime 中。要进行下一步更改，请更改 *max-step*

加载文件以运行代码（批处理模式）

(load  "apollonian.lisp")

; first run
;(require :asdf)
;(require :asdf-install)
;(asdf-install:install :zpng)
;(asdf-install:install :Vecto)
; you must press 2 and 0 when the program asks

; next times load packages from disk
(asdf:operate 'asdf:load-op 'vecto)

(in-package vecto)

;-----------------------------------------------------------------------
;---------------------------- definitions of functions ---------------
;-----------------------------------------------------------------------

; kc is a list describing circle (list k c)  where k is curvature and c is a center ( complex number)
; k can be positive ( inner circle) , negative ( outer circle) or zero ( =  line )

(defun draw-vecto-circle (kc)
  (let* ((c (second kc))
	 (r (abs (/ 1 (first kc)))))	; r = abs(1/k)
    (centered-circle-path (realpart c) (imagpart c) r))) ; vecto

; Desfirsttes' circle theorem 
(defun solve-equation-m (k1 k2 k3)
  (- (+ k1 k2 k3 ) (* 2 (sqrt (+ (* k1 k2) (* k2 k3) (* k1 k3))))))

(defun solve-equation-p (k1 k2 k3)
  (+ (+ k1 k2 k3 ) (* 2 (sqrt (+ (* k1 k2) (* k2 k3) (* k1 k3))))))

; compute, draws and gives back 4-th circle usind solve-equation-p and solve-equation-p
(defun draw-forth-circle-pp (kc1 kc2 kc3)
  (let* ((k1 (first kc1))
	 (k2 (first kc2))
	 (k3 (first kc3))
	 (p1 (* k1 (second kc1))) ; pn = kn * cn 
	 (p2 (* k2 (second kc2)))
	 (p3 (* k3 (second kc3)))
	 (k4 (solve-equation-p k1 k2 k3)) ; find k
	 (c4 (/ (solve-equation-p p1 p2 p3) k4)) ; find c
	 (kc4 (list k4 c4)))
    (draw-vecto-circle kc4) ; draw 
    kc4)) ; return 4-th circle

; compute, draws and gives back 4-th circle usind solve-equation-p and solve-equation-m
(defun draw-forth-circle-pm (kc1 kc2 kc3)
  (let* ((k1 (first kc1))
	 (k2 (first kc2)) 
	 (k3 (first kc3))
	 (p1 (* k1 (second kc1)))
	 (p2 (* k2 (second kc2)))
	 (p3 (* k3 (second kc3)))
	 (k4   (solve-equation-p k1 k2 k3))
	 (c4 (/ (solve-equation-m p1 p2 p3) k4))
	 (kc4 (list k4 c4)))
    (draw-vecto-circle kc4)
    kc4))

; easy = pp
(defun fill-easy-gap (kc1 kc2 kc3 steps)
  (when (> steps 0)
      (let* ((kc4 (draw-forth-circle-pp kc1 kc2 kc3))) ; 4-th circle
	(fill-easy-gap kc1 kc2 kc4 (- steps 1)) ; 3 subgaps
	(fill-easy-gap kc2 kc3 kc4 (- steps 1))  
	(fill-easy-gap kc3 kc1 kc4 (- steps 1)))))

; only for gap 1c = hard gap
(defun fill-hard-gap (kc-ic kc-ia kc-0out steps)
  (let* (kc-1c kc-2cc  kc-3ccc  kc-4ccca kc-5cccac) ; hard circles , also kc-6cccacc
    ;------------ gap 1c --------------------------------------------   
    (when (> steps 0) (setq kc-1c (draw-forth-circle-pm kc-ic kc-ia kc-0out)) 						; kc-1c hard
	  (fill-easy-gap kc-ia kc-0out kc-1c (- steps 1))								; kc-2ca
	  (fill-easy-gap kc-ia kc-ic kc-1c (- steps 1))									; kc-2cb
	  ; ----------- hard subgap 2cc ------------------------------------
	  (when (> steps 1)  (setq kc-2cc (draw-forth-circle-pm kc-ic kc-0out kc-1c))					; kc-2cc hard
		(fill-easy-gap kc-0out kc-1c kc-2cc (- steps 2))							; kc-3cca
		(fill-easy-gap kc-ic kc-1c kc-2cc (- steps 2))	        						; kc-3ccb
		; ----------- hard subgap 3ccc ------------------------------------
		(when (> steps 2)   (setq kc-3ccc (draw-forth-circle-pm kc-ic kc-0out kc-2cc))				; kc-3ccc hard
		      (fill-easy-gap kc-ic kc-2cc kc-3ccc (- steps 3))							; kc-4cccb
		      (fill-easy-gap kc-ic kc-0out kc-3ccc (- steps 3))							; kc-4cccc
		      ; ----------- hard subgap 4ccca ------------------------------------
		      (when (> steps 3)  (setq kc-4ccca (draw-forth-circle-pm kc-0out kc-2cc kc-3ccc))			; kc-4ccca hard
			    (fill-easy-gap kc-0out kc-2cc kc-4ccca (- steps 4))						; kc-5cccaa
			    (fill-easy-gap kc-2cc kc-3ccc kc-4ccca (- steps 4))						; kc-5cccab
			    (when (> steps 4) (setq kc-5cccac (draw-forth-circle-pm kc-0out kc-3ccc kc-4ccca)))))))))   ; kc-5cccac hard

; example of use : (draw-apollonian-gasket "a.png" 800 2)
; classical Desfirsttes configuration : 3 mutually tangent circles and 4-th inside ( and fith outside)
(defun draw-apollonian-gasket-n3 (file side step)
  (with-canvas (:width side :height side) ; vecto
	       (set-rgb-stroke 0 0 0) ; vecto
	       (set-line-width 1) ; vecto

	       
	      (let* (	(r0out (/ side 2))
			(k0out (- (/ 1 r0out)))
			(c0out (complex r0out r0out))
			(kc0out (list k0out c0out)) ; list defining circle 
					; a1:float(1 + 2 / sqrt(3)),  http://www2.stetson.edu/~efriedma/cirincir/ 
			(a (+ 1 (/ 2 (sqrt 3))))
			(ri   (/ r0out a)) ; three equal inner circles = initial circles
			(ki (/ 1 ri))	
			(cia (complex r0out (- side ri))) ; one circle in upper row
			(kcia (list ki cia))
			(h (* ri (sqrt 3))) ; height of equilateral triangle with side = 2*ri
					; 2 circles in lower row
			(cib (complex  (+ r0out ri) (- side (+ h ri))))
			(cic (complex  (- r0out ri) (- side (+ h ri))))
			(kcib (list ki cib))
			(kcic (list ki cic))
			kc0in ) 
			; drawing code
			; step -1 = three equal inner circles
		 (draw-vecto-circle kcia ) 		; ia
		 (draw-vecto-circle kcib ) 		; ib
		 (draw-vecto-circle kcic ) 		; ic
			; step 0 = outer and most inner circle
		 (draw-vecto-circle kc0out )		; 0out
		 (setq kc0in ( draw-forth-circle-pp kcia kcib kcic )) ; 0in
			; this is starting configuration. 
			; One can go to the next steps now
			; Fill 6 gaps :   
			; 3 peripheral gaps
		 (fill-easy-gap kcia kcib kc0out step) ; 1a
		 (fill-easy-gap kcib kcic kc0out step) ; 1b	
		 (fill-hard-gap kcic kcia kc0out step) ; 1c
			; 3 medial gaps
		 (fill-easy-gap kcia kcib kc0in step)  ; 1d
		 (fill-easy-gap kcib kcic kc0in step)  ; 1e
		 (fill-easy-gap kcic kcia kc0in step)  ; 1f
			; rest of drawing code
		 (stroke)) ; before save ( vecto procedure)
	       (print (save-png file)))) ; info text and vecto procedure

;---------------compile ---------------------------------
(compile 'draw-vecto-circle )
(compile 'solve-equation-m)
(compile 'solve-equation-p)
(compile 'draw-forth-circle-pp)
(compile 'draw-forth-circle-pm)
(compile 'fill-easy-gap)
(compile 'fill-hard-gap)
(compile 'draw-apollonian-gasket-n3)

;----------global var ----------------------

(defparameter *max-step* 0 " maximal step of drawing apollonian gasket from. It is an integer >= 0 ")

(defparameter *file-name*
  (make-pathname 
   :name (concatenate 'string "apollonian-n3-s" (write-to-string *max-step*))
   :type "png")
  "name (or pathname) of png file ")

;====================================== run ==================================
(draw-apollonian-gasket-n3 *file-name* 800 *max-step*)

JavaScript

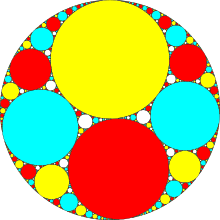
这是一个增量算法，它维护着一个包含三个相互接触的圆的队列。主循环从队列的开头开始，移除一个三元组，用所需的圆形填充它，将生成的圆形添加到一个用于绘制为 SVG 的圆形列表中，并将添加圆形后产生的三个三元组添加到计算队列的末尾。作为额外功能，这些圆形被着色，因此没有两个相邻的圆形具有相同的颜色。

用法：将两个 SVG 模板部分和中间的 Javascript 部分合并到一个 SVG 文件中，并加载到网页浏览器（或另一个支持 Javascript 或 ECMAScript 的 SVG 浏览器）中。

<?xml version="1.0" encoding="UTF-8"?>
<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg
 xmlns="http://www.w3.org/2000/svg"
 xmlns:xlink="http://www.w3.org/1999/xlink"
 width="100%" height="100%" viewBox="0 0 768 768"
 onload="init(evt)"
><title>Apollonian Fractal</title
><desc>Randomized Apollonian fractal circle packing</desc
><script type="text/ecmascript"><![CDATA[

// SVG properties
var ns = "http://www.w3.org/2000/svg";
var xns = "http://www.w3.org/1999/xlink";
var SVGDocument = null;
var size = 768; // should match 'viewBox'
var minsize = 0.001;

// convert internal coordinates and lengths to SVG
function coord(x) { return x*size/2 + size/2; }
function dist(d) { return d*size/2; }

// complex numbers
function C(r,i)    { this.r = r; this.i = i; }
function Cconj(c)  { return new C(c.r, -c.i); }
function Cadd(c,d) { return new C(c.r+d.r,c.i+d.i); }
function Csub(c,d) { return new C(c.r-d.r,c.i-d.i); }
function Cmul(c,d) { return new C(c.r*d.r-c.i*d.i,c.r*d.i+c.i*d.r); }
function Csqrt(c)  { return new C(Math.sqrt(Math.sqrt(c.r*c.r+c.i*c.i)) * Math.cos(Math.atan2(c.i,c.r)/2),
                                  Math.sqrt(Math.sqrt(c.r*c.r+c.i*c.i)) * Math.sin(Math.atan2(c.i,c.r)/2)); }

// sort points into order
function clockwise(a, b, c) {
  var x1 = a.x-b.x; var y1 = a.y-b.y;
  var x2 = c.x-b.x; var y2 = c.y-b.y;
  if ((x1*y2-y1*x2) >= 0) return [a,b,c]; else return [a,c,b];
}

// compute the 4th circle touching 3 circles, each of which touch the other two
function Kiss(a, b, c, initial) {
  var k1 = 1 / a.r; var z1 = new C(a.x, a.y); var kz1 = Cmul(new C(k1,0),z1);
  var k2 = 1 / b.r; var z2 = new C(b.x, b.y); var kz2 = Cmul(new C(k2,0),z2);
  var k3 = 1 / c.r; var z3 = new C(c.x, c.y); var kz3 = Cmul(new C(k3,0),z3);
  var k4p = k1 + k2 + k3 + 2*Math.sqrt(k1*k2 + k2*k3 + k3*k1);
  var k4m = k1 + k2 + k3 - 2*Math.sqrt(k1*k2 + k2*k3 + k3*k1);
  var kz4p = Cadd(Cadd(Cadd(kz1,kz2),kz3),Cmul(new C(2,0),
    Csqrt(Cadd(Cadd(Cmul(kz1,kz2),Cmul(kz2,kz3)),Cmul(kz3,kz1)))));
  var kz4m = Csub(Cadd(Cadd(kz1,kz2),kz3),Cmul(new C(2,0),
    Csqrt(Cadd(Cadd(Cmul(kz1,kz2),Cmul(kz2,kz3)),Cmul(kz3,kz1)))));
  var k4;
  var kz4;
  var k4b;
  var kz4b;
  var cs = new Array();
  if (k4p > k4m) { k4 = k4p; kz4 = kz4p; k4b = k4m; kz4b = kz4m; }
  else           { k4 = k4m; kz4 = kz4m; k4b = k4p; kz4b = kz4p; }
  var cc = new Circle(kz4.r/k4,kz4.i/k4,Math.abs(1/k4), 6 - a.colour - b.colour - c.colour);
  var dx = a.x - cc.x
  var dy = a.y - cc.y
  var dr = a.r + cc.r
  if (Math.abs(dx * dx + dy *dy - dr * dr) > 0.0001) {
    cc = new Circle(kz4b.r/k4,kz4b.i/k4,Math.abs(1/k4), 6 - a.colour - b.colour - c.colour);
  }
  cs[cs.length] = cc;
  if (initial) {
    cc = new Circle(kz4b.r/k4b,kz4b.i/k4b,Math.abs(1/k4b), 6 - a.colour - b.colour - c.colour);
    cs[cs.length] = cc;
  }
  return cs;
}

// called once on load
function init(evt) {
  // get document
  SVGDocument = evt.target.ownerDocument;

  // initial bounding circle
  var b = new Circle(0, 0, -1, 0);

  // insert two randomly positioned touching circles
  var tr = 1-Math.random()/2;
  var pa = Math.PI/2 - Math.asin(Math.random()*(1-tr)/tr);
  var px = tr * Math.cos(pa);
  var py = tr * Math.sin(pa);
  var pr = 1 - tr;
  var qr = (1 - pr) * (1 - Math.cos(pa + Math.PI/2))
         / (1 + pr - (1 - pr) * Math.cos(pa + Math.PI/2));
  var qx = 0;
  var qy = qr - 1;
  var p = new Circle(px, py, pr, 1);
  var q = new Circle(qx, qy, qr, 2);

  // a queue to contain triples of touching circles
  var queue = new Array();
  var cs = Kiss(b,p,q, true);
  queue[queue.length] = [b,p,cs[0]];
  queue[queue.length] = [b,cs[0],q];
  queue[queue.length] = [cs[0],p,q];
  queue[queue.length] = [b,p,cs[1]];
  queue[queue.length] = [b,cs[1],q];
  queue[queue.length] = [cs[1],p,q];

  // a queue to contain circles to draw
  var draw = new Array();
  draw[draw.length] = b;
  draw[draw.length] = p;
  draw[draw.length] = q;
  draw[draw.length] = cs[0];
  draw[draw.length] = cs[1];

  // add 10000 more circles to the draw queue
  // adding new triples to the compute queue
  var c;
  for (c = 0; c < Math.min(queue.length, 10000); c = c + 1) {
    var c0 = queue[c][0];
    var c1 = queue[c][1];
    var c2 = queue[c][2];
    var ncs = Kiss(c0,c1,c2);
    var nc = ncs[0];
    if (nc.r > minsize) {
      queue[queue.length] = [nc,c1,c2];
      queue[queue.length] = [c0,nc,c2];
      queue[queue.length] = [c0,c1,nc];
      draw[draw.length] = nc;
    }
  }

  // add all generated circles to an SVG <g> element
  var g = SVGDocument.createElementNS(ns, "g");
  g.setAttributeNS(null, "stroke", "black");
  g.setAttributeNS(null, "stroke-width", "1");
  var i;
  for (i = 0; i < draw.length; i = i + 1) {
    g.appendChild(draw[i].draw());
  }

  // link the <g>s into the DOM so they are displayed
  var svg = SVGDocument.documentElement;
  svg.appendChild(g);

} // init()

// circle class
function Circle(x, y, r, colour) {
  // properties of a circle
  this.x = x;
  this.y = y;
  this.r = r;
  this.colour = colour;
  // convert to svg
  this.draw = function() {
    var colours = ["white", "red", "yellow", "cyan"];
    var c = SVGDocument.createElementNS(ns, "circle");
    c.setAttributeNS(null, "fill", colours[this.colour]);
    c.setAttributeNS(null, "cx", coord(this.x));
    c.setAttributeNS(null, "cy", coord(this.y));
    c.setAttributeNS(null, "r",  dist(this.r));
    return c;
  };
} // Circle()