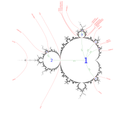
分形/复平面迭代/曼德勃罗集内部
外观
< 分形
(重定向自 分形/复平面迭代/曼德勃罗集)本书展示了如何为绘制参数平面[1](曼德勃罗集[2])编写不同的算法,用于复二次多项式。[3]
人们可以在参数平面上找到不同类型的点/集。[4]
此页面介绍了曼德勃罗集的内部点。[5]
The “capture-time algorithm” is a natural counterpart for points inside the set to the “escape-time algorithm”. Given some desired tolerance, the orbit P is generated for each point c ∈ C until some point in the orbit is closer than to some previous point in the orbit. The number of iterations needed for this to occur is mapped to a color and displayed at the pixel corresponding to c. Adam Cunningham[6]
-
整个集合
-
迷你曼德勃罗集
-
实二次映射
数学方程 :[7]
其中
表示 f 相对于 z 的一阶导数
另请参阅
JPBotelho 的 HLSL 代码[10]
Shader "Fractals/Coloring Techniques/Escape-Time"
{
Properties
{
_MainTex ("Texture", 2D) = "white" {}
_Iter ("Iterations", Range(0, 250)) = 100
_Dividend ("Dividend", Range (0, 0.5)) = 15
_Zoom ("Zoom", Range (0.1, 1000)) = 0.65
_Position ("Offset", Vector) = (0.4, 0, 0, 0)
_Background ("Background", Color) = (0, 0.25, 1, 0)
_Origin ("Origin", Color) = (0, 0, 0, 0)
}
SubShader
{
Cull Off ZWrite Off ZTest Always
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
#include "Complex.cginc"
#include "FractalOperations.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
float4 vertex : SV_POSITION;
};
sampler2D _MainTex;
int _Iter;
fixed _Zoom;
fixed _Dividend;
float2 _Position;
fixed4 _Background;
fixed4 _Origin;
v2f vert (appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = v.uv;
return o;
}
fixed4 frag (v2f i) : SV_Target
{
float x0 = (ClampScaleX(i.uv) + _Position.x) / _Zoom;
float y0 = (ClampScaleY(i.uv) + _Position.y) / _Zoom;
float2 z = float2(x0, y0);
float2 c = float2(x0, y0);
int iteration = 0;
float l = 0;
while (IsBounded(z, 40) && iteration < _Iter)
{
l += log (cabs(2 * z));
z = cmul(z, z);
z += c;
iteration++;
}
l /= iteration;
if (l > 0)
return _Background;
float3 color = tanh(l >= 0 ?
float3(0, 0.7 * log(1 + l), log(1 + l)) :
3 * float3(_Origin.x-l, _Origin.y-l * 0.1, _Origin.z));
return float4(color + _Dividend, 1);
}
ENDCG
}
}
CustomEditor "FractalEditor"
}

# Hypercomputing the Mandelbrot Set? by Petrus H. Potgieter February 1, 2008
n=1000; # For an nxn grid
m=50; # Number of iterations
c=meshgrid(linspace(-2,2,n))\ # Set up grid
+i*meshgrid(linspace(2,-2,n))’;
x=zeros(n,n); # Initial value on grid
for i=1:m
x=x.^2+c; # Iterate the mapping
endfor
imagesc(min(abs(x),2.1)) # Plot monochrome, absolute
# value of 2.1 is escape
点的颜色
- 与 z 在最后一次迭代时的值成正比。
- 显示了周期性吸引子的内部水平集。
bof60 的图像位于“分形的美丽”这本书的第 60 页。方法描述在 bof 的第 63 页。它仅用于曼德勃罗集的内部点。
点的颜色与
- 其轨道到原点[11][12]的最小距离成正比
- 迭代过程中 z 获得的最小值[13]
- 阐明了原点(临界点)的迭代在集合内部到原点的最近距离
- “每个视频帧的每个像素都代表一个特定的复数 c = a + ib。对于每个连续帧 n,z(c,n) := z(c, n-1)^2 + c 的幅度显示为这些点 c 中的每个点的灰度强度值:幅度较大的点更白,幅度较小的点更暗。当 n 从 1 增加到 256 时,曼德勃罗集外部的点会迅速饱和为纯白色,而曼德勃罗集内部的点会在较暗的强度之间振荡。” 布莱恩·高沃特[14]
距离的水平集是具有相同距离的点集。[15]
if (Iteration==IterationMax)
/* interior of Mandelbrot set = color is proportional to modulus of last iteration */
else { /* exterior of Mandelbrot set = black */
color[0]=0;
color[1]=0;
color[2]=0;
}
- 代码片段 : 来自 Gnofract4d 的 fractint.cfrm[16]
bof60 {
init:
float mag_of_closest_point = 1e100
loop:
float zmag = |z|
if zmag < mag_of_closest_point
mag_of_closest_point = zmag
endif
final:
#index = sqrt(mag_of_closest_point) * 75.0/256.0
}
另请参阅
- Bof61
-
动画
-
2D
-
3D

曼德勃罗集的双曲分量的周期是临界轨道的极限集的周期。
用于计算周期的算法
- 直接从动力学平面上的临界点 z = 0.0 的迭代中检测周期
- “快速而肮脏”算法:检查是否,则将 c 点用颜色 n 着色。这里 n 是吸引轨道的周期,eps 是吸引点周围圆的半径 = 数值计算的精度
- “如果正确实现,基于区间算术的方法能够找到相当大的 n 的所有周期 n 循环。” (ZBIGNIEW GALIAS)[17]
- Floyd 的循环查找算法[18]
- 蜘蛛算法
- 原子域,BOF61
- 周期检测
内部检测
[edit | edit source]如果以下所有内容都成立,则像素很有可能是内部[19]
- 像素被标记为内部(黑色)
- 所有周围的像素都被标记为内部(黑色)
- 所有黑色像素具有相同的周期
内部坐标和乘数映射
[edit | edit source]

克劳德·海兰德-艾伦的算法
- 检查 c
- 当 c 在曼德布罗集之外时
- 现在放弃
- 或使用外部坐标
- 当 c 不在外部(在内部或边界上)时:对于每个周期 p,从 1 开始并递增
- 找到周期点 z0,使得 fp(z0,c)=z0,使用牛顿法在一个复变数中
- 通过在 z0 处对 fp 关于 z 的一阶导数进行求值来找到 b
- 如果 |b|≤1,则返回 b,否则继续下一个 p
- 当 c 在曼德布罗集之外时
计算
[edit | edit source]对于周期:[23]
- 1 到 3 可以使用显式方程[24]
- >3 必须使用数值方法来找到
周期 1
[edit | edit source]从边界方程开始
c+(w/2)^2-w/2=0;
并针对 w 求解
(%i1) eq1:c+(w/2)^2-w/2=0;
2
w w
(%o1) -- - - + c = 0
4 2
(%i2) solve(eq1,w);
(%o2) [w = 1 - sqrt(1 - 4 c), w = sqrt(1 - 4 c) + 1]
(%i3) s:solve(eq1,w);
(%o3) [w = 1 - sqrt(1 - 4 c), w = sqrt(1 - 4 c) + 1]
(%i4) s:map(rhs,s);
(%o4) [1 - sqrt(1 - 4 c), sqrt(1 - 4 c) + 1]
所以
w = w(c) = 1.0 - csqrt(1.0-4.0*c)
周期 2
[edit | edit source]w = 4.0*c + 4;
周期 3
[edit | edit source]
它可以使用 Maxima CAS 求解
(%i1) e1:c^3 + 2*c^2 - (w/8-1)*c + (w/8-1)^2 = 0;
3 2 w w 2
(%o1) c + 2 c + (1 - -) c + (- - 1) = 0
8 8
(%i2) solve(e1,w);
(%o2) [w = (- 4 sqrt((- 4 c) - 7) c) + 4 c + 8, w = 4 sqrt((- 4 c) - 7) c + 4 c + 8]
数值逼近
[edit | edit source]complex double AproximateMultiplierMap(complex double c, int period, double eps2, double er2)
{
complex double z; // variable z
complex double zp ; // periodic point
complex double zcr = 0.0; // critical point
complex double d = 1;
int p;
// first find periodic point
zp = GivePeriodic( c, zcr, period, eps2, er2); // Find periodic point z0 such that Fp(z0,c)=z0 using Newton's method in one complex variable
// Find w by evaluating first derivative with respect to z of Fp at z0
if ( cabs2(zp)<er2) {
z = zp;
for (p=0; p < period; p++){
d = 2*z*d; /* first derivative with respect to z */
z = z*z +c ; /* complex quadratic polynomial */
}}
else d= 10000; //
return d;
}
另请参阅
内角
[edit | edit source]
Renato Fonseca 的方法:[25] “集合中的一个点 c 的色调等于参数
(适当缩放,以便最终得到 0 到 255 范围内的数字)。数字 z_nmax 是 z 序列中计算的最后一个数字。”
另请参阅
Fractint
[edit | edit source]Fractint:颜色参数:INSIDE=ATAN
颜色通过确定最后一次迭代值相对于实轴的角度(以度为单位)并使用绝对值来确定。此功能应与 periodicity=0[26] 一起使用
内部射线
[edit | edit source]沿着内部射线从双曲参数到抛物线参数[27]
-
内部和外部射线
-
乘数映射和内部射线
-
内部和外部射线
当 变化而 保持不变时, 沿着 内部射线 移动。 [28] 它被用作曼德勃罗集内部的 路径。
double complex Give_c(double t, double r, int p)
{
/*
input:
InternalRadius = r in [0,1]
InternalAngleInTurns = t in range [0,1]
p = period
output = c = complex point of 2D parameter plane
*/
complex double w = 0.0;
complex double c = 0.0;
t = t*2*M_PI; // from turns to radians
// point of unit circle
w = r* cexp(I*t);
// map circle to component
switch (p){
case 1: c = (2.0*w - w*w)/4.0; break;
case 2: c = (w -4.0)/ 4.0; break;
}
return c;
}
/* find c in component of Mandelbrot set
uses complex type so #include <complex.h> and -lm
uses code by Wolf Jung from program Mandel
see function mndlbrot::bifurcate from mandelbrot.cpp
http://www.mndynamics.com/indexp.html
*/
double complex GiveC(double InternalAngleInTurns, double InternalRadius, unsigned int period)
{
//0 <= InternalRay<= 1
//0 <= InternalAngleInTurns <=1
double t = InternalAngleInTurns *2*M_PI; // from turns to radians
double R2 = InternalRadius * InternalRadius;
double Cx, Cy; /* C = Cx+Cy*i */
switch ( period ) {
case 1: // main cardioid
Cx = (cos(t)*InternalRadius)/2-(cos(2*t)*R2)/4;
Cy = (sin(t)*InternalRadius)/2-(sin(2*t)*R2)/4;
break;
case 2: // only one component
Cx = InternalRadius * 0.25*cos(t) - 1.0;
Cy = InternalRadius * 0.25*sin(t);
break;
// for each period there are 2^(period-1) roots.
default: // safe values
Cx = 0.0;
Cy = 0.0;
break; }
return Cx+ Cy*I;
}
// draws points to memory array data
int DrawInternalRay(double InternalAngleInTurns, unsigned int period, int iMax, unsigned char data[])
{
complex double c;
double InternalRadius;
double RadiusStep; // between radius of points
int i; // number of point to draw
RadiusStep = 1.0/iMax;
for(i=0;i<=iMax;++i){
InternalRadius = i * RadiusStep;
c = GiveC(InternalAngleInTurns, InternalRadius, period);
DrawPoint(c,data);
}
return 0;
}
示例:角度为 1/6 的主心形的内部射线。
内角
射线的半径
单位圆的内部半径点
将点 映射到参数平面
对于 ,这是主心形的方程。
当 保持不变而 变化时, 沿着内部曲线移动。
/* find c in component of Mandelbrot set
uses complex type so #include <complex.h> and -lm
uses code by Wolf Jung from program Mandel
see function mndlbrot::bifurcate from mandelbrot.cpp
http://www.mndynamics.com/indexp.html
*/
double complex GiveC(double InternalAngleInTurns, double InternalRadius, unsigned int period)
{
//0 <= InternalRay<= 1
//0 <= InternalAngleInTurns <=1
double t = InternalAngleInTurns *2*M_PI; // from turns to radians
double R2 = InternalRadius * InternalRadius;
double Cx, Cy; /* C = Cx+Cy*i */
switch ( period ) {
case 1: // main cardioid
Cx = (cos(t)*InternalRadius)/2-(cos(2*t)*R2)/4;
Cy = (sin(t)*InternalRadius)/2-(sin(2*t)*R2)/4;
break;
case 2: // only one component
Cx = InternalRadius * 0.25*cos(t) - 1.0;
Cy = InternalRadius * 0.25*sin(t);
break;
// for each period there are 2^(period-1) roots.
default: // safe values
Cx = 0.0;
Cy = 0.0;
break;
}
return Cx+ Cy*I;
}
// draws points to memory array data
int DrawInternalCurve(double InternalRadius , unsigned int period, int iMax, unsigned char data[])
{
complex double c;
double InternalAngle; // in turns = from 0.0 to 1.0
double AngleStep;
int i;
// int iMax =100;
AngleStep = 1.0/iMax;
for (i=0; i<=iMax; ++i) {
InternalAngle = i * AngleStep;
c = GiveC(InternalAngle, InternalRadius, period);
DrawPoint(c,data);
}
return 0;
}
教程
- 在 Basic 中,请参见 Mandelbrot Dazibao
- 在 Java 中,请参见 Evgeny Demidov
- 在 C 中,请参见 Linas Vepstas
- 在 C++ 中,请参见 Wolf Jung 页面,
- 在 Factor 中,请参见由 Slava Pestov 编写的 程序
- 在 Gnuplot 中,请参见由 T.Kawano 编写的 教程
- 在 Lisp(Maxima)中,请参见
- Jaime E. Villate 编写的 Dynamics
- Robert P. Munafo 编写的 Mu-Ency - 曼德勃罗集百科全书
- Yannick Gingras 编写的 Frac,以及其精美的 [1] 图像库
- Takaya Iwamoto 编写的 Lisp 中的分形
- 在 Octave 中,请参见 华夏公益教科书 或由 Christopher Wellons 编写的另一个版本
- 如何手动绘制曼德勃罗集
- 各种语言的比较
- 计算机语言基准游戏:使用 ≈12 个有缺陷的基准测试,比较 ≈30 种编程语言在 4 种不同的操作系统/机器组合下的性能。
- rosettacode
- 由 Erik Wrenholt 编写的,在 Ruby、Io、PHP、Python、Lua、Java、Perl、Applescript、TCL、ELisp、Javascript、OCaml、Ghostscript 和 C 中的 分形基准测试
- 由 Xavier Calbet 编写的,在 PDL、IDL、MATLAB、Octave、C 和 FORTRAN77 中
- ASCII 图形:[29]
- Robert P. Munafo 编写的,在 Mu-Ency 上的 ASCII 图形
- 由 Warp 编写的,使用脚本语言
- Theo Wollenleben 编写的分形基准测试
- 在 Bill Clementson 的博客 上,使用 Lisp
- 3D
-
这是图像“Mandel zoom 03 seehorse.jpg” DEM 的 3D 版本。
-
半 3D 超复数 Mandelbrot 分形。使用 Mandelbulber 0.80 渲染。
- ↑ 维基百科中的参数平面
- ↑ 维基百科中的 Mandelbrot 集
- ↑ 维基百科中的复二次多项式
- ↑ reenigne 博客:mandelbrot-set-taxonomy
- ↑ 通过 A Cunningham 展示 Mandelbrot 集的内部结构(带有 python 3 程序和代码)
- ↑ Adam Cunningham 展示 Mandelbrot 集的内部结构
- ↑ 2013 年 10 月 4 日,Didier Gonze 的逻辑方程
- ↑ janthor 的 Lyapunov 指数和 Mandelbrot 集
- ↑ Anders Sandberg 的图像
- ↑ github 库 JPBotelho:Fractal-Megacollection(Unity 的 HLSL 着色器)
- ↑ Fractint:各种选项和算法
- ↑ Java™ Number Cruncher:Java 程序员的数值计算指南,作者 Ronald Mak
- ↑ Firefly 应用程序帮助,作者 Terry W. Gintz
- ↑ Mandelbrot 振荡,作者 Brian Gawalt
- ↑ Fractint 文档,作者 Noel Giffin
- ↑ gnofract4d
- ↑ 使用区间方法对电子电路中的周期轨道进行严格研究,作者 Zbigniew Galias
- ↑ Milan 的 Mandelbrot 集绘制
- ↑ fractalforums.org:使用级数逼近确定跳过的最佳迭代次数
- ↑ Mandelbrot 集内部坐标,作者 Claude Heiland-Allen
- ↑ 内部距离渲染实践,作者 Claude Heiland-Allen
- ↑ math.stackexchange 问题:测试 Mandelbrot 球中周期为 n 的成员资格/1151953#1151953
- ↑ Brown 方法,作者 Robert P. Munafo,2003 年 9 月 22 日。
- ↑ 精确坐标,作者 Robert P. Munafo,2003 年 9 月 22 日。
- ↑ Mandelbrot 集,作者 Renato Fonseca
- ↑ fractint 颜色参数
- ↑ 沿着内射线的双曲参数到抛物线参数,作者 Yi-Chiuan Chen 和 Tomoki Kawahira
- ↑ 维基百科中的内部射线
- ↑ ASCII 图形