交通基础/土方工程

土方工程是交通项目很少能避免的。为了建立一个正常运行的道路，地形通常需要进行调整。在许多情况下，几何设计通常涉及最大限度地降低土方移动的成本。土方工程用体积单位表示（公制单位为立方米）。体积的增加需要额外的卡车（或同一卡车的更多行程），这会花费金钱。因此，设计师必须设计出土方工程量非常少的道路。

横断面和体积计算

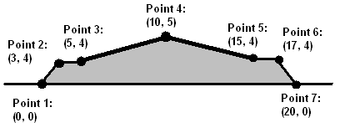
为了确定某一特定地点的土方工程量，必须计算体积。对于线性设施（包括高速公路、铁路、跑道等），体积可以通过将整个走廊长度的横断面面积（垂直于中心线的切片）积分来轻松计算。更简单地说，可以在走廊上选择几个横断面，并对整个长度取平均值。有几种不同的程序可以用来计算土方工程横断面的面积。过去，流行的方法是手工绘制横断面，并使用描迹仪测量面积。在现代，计算机使用坐标法来评估土方工程计算。为了执行此任务，需要在横断面周围识别具有已知高程的点。这些点在 (X, Y) 坐标平面中被认为是，其中 X 表示平行于地面的水平轴，Y 表示垂直轴，即高程。可以使用以下公式计算面积

$A=|{\frac {1}{2}}\sum \limits _{i=1}^{n}{X_{i}(Y_{i+1}-Y_{i-1})}|\,\!$

其中

$A\,\!$ = 横断面面积
$n\,\!$ = 横断面上点的数量（注意：n+1 = 1 且 1-1=n，用于索引）
$X\,\!$ = X 坐标
$Y\,\!$ = Y 坐标

有了这些，就可以计算土方工程量。最简单的方法是使用平均端面法，即在它们之间的整个长度上对两个端面取平均值。

$V={\frac {A_{1}+A_{2}}{2}}L\,\!$

其中

$V\,\!$ = 体积
$A_{1}\,\!$ = 第一面横断面面积
$A_{2}\,\!$ = 第二面横断面面积
$L\,\!$ = 两个面积之间的长度

如果一个端面面积的值为零，则土方工程量可以被认为是金字塔，正确的公式为

$V={\frac {AL}{3}}\,\!$

一个更准确的公式是棱柱体公式，它消除了平均端面法所累积的大部分误差。

$V_{p}={\frac {L(A_{1}+4A_{m}+A_{2})}{6}}\,\!$

其中

$V_{p}\,\!$ = 棱柱公式给出的体积
$A_{m}\,\!$ = 两个横截面之间中点平面的面积

挖方和填方

道路设计中的各个路段需要填土。其他路段需要挖土。填入的土被称为填方，而移除的土被称为挖方。通常，设计师会绘制名为挖方/填方图的图纸，以说明在任何给定地点存在的挖方或填方情况。该图纸非常标准，仅仅是一个图表，其中 X 轴表示位置，Y 轴的正值范围表示填方，而负值范围表示挖方。

土方平衡

使用挖方和填方数据，可以计算出总体土方平衡。土方平衡表示根据设计在该地点到该点为止的剩余土方总量（如果为正）或需要土方总量（如果为负）。这是一个有用的信息，因为它可以确定项目完成时剩余土方或需要土方的数量，从而允许设计师计算出运出多余土方或运入所需土方的成本。此外，图形表示的土方平衡图可以帮助设计师在内部移动土方以节省资金。

与挖方/填方图类似，土方平衡图也绘制在两个轴上。X 轴表示沿着道路走廊的位置，Y 轴表示土方数量，可以是多余的（正）或需要的（负）。

演示

示例

示例 1：计算体积

TProblem

问题

要在平坦的地形上设计一条道路。这条道路长 150 米。选择了四个横截面，分别位于 0 米、50 米、100 米和 150 米处。这些横截面的面积分别为 40 平方米、42 平方米、19 平方米和 34 平方米。这条道路需要多少土方量？

示例

解决方案

在所有这些横截面之间存在三个路段。由于没有一个路段以面积为零结束，因此可以使用平均端面积法。可以计算出各个路段的体积，然后将它们加起来。

0 到 50 米之间的路段

$V={\frac {A_{1}+A_{2}}{2}}L={\frac {40\ \mathrm {m^{2}} +42\ \mathrm {m^{2}} }{2}}\cdot 50\ \mathrm {m} =2050\ \mathrm {m^{3}} \,\!$

50 到 100 米之间的路段

$V={\frac {A_{1}+A_{2}}{2}}L={\frac {42\ \mathrm {m^{2}} +19\ \mathrm {m^{2}} }{2}}\cdot 50\ \mathrm {m} =1525\ \mathrm {m^{3}} \,\!$

100 到 150 米之间的路段

$V={\frac {A_{1}+A_{2}}{2}}L={\frac {19\ \mathrm {m^{2}} +34\ \mathrm {m^{2}} }{2}}\cdot 50\ \mathrm {m} =1325\ \mathrm {m^{3}} \,\!$

计算得出总土方量为

$2050\ \mathrm {m^{3}} +1525\ \mathrm {m^{3}} +1325\ \mathrm {m^{3}} =4900\ \mathrm {m^{3}} \,\!$

示例 2：质量平衡

TProblem

问题

假设在 10 米长的非常非常丘陵地形上建造的道路，每米沿线的开挖/填筑剖面如下，估计该项目剩余或需要的土方量。

0 米：3 米填筑
1 米：1 米填筑
2 米：2 米开挖
3 米：5 米开挖
4 米：7 米开挖
5 米：8 米开挖
6 米：2 米开挖
7 米：1 米填筑
8 米：3 米填筑
9 米：6 米填筑
10 米：7 米填筑

示例

解决方案

如果“开挖”被视为可用土方的剩余，“填筑”被视为可用土方的减少，问题就变成了简单的加减运算。

$[(-3\ \mathrm {m} )+(-1\ \mathrm {m} )+2\ \mathrm {m} +5\ \mathrm {m} +7\ \mathrm {m} +8\ \mathrm {m} +2\ \mathrm {m} +(-1\ \mathrm {m} )+(-3\ \mathrm {m} )+(-6\ \mathrm {m} )+(-7\ \mathrm {m} )]\cdot 1\ \mathrm {m^{2}} =3\ \mathrm {m^{3}} \,\!$

剩余 3 立方米土方。

思考题

问题

如果发现质量平衡确实是平衡的（最终值为零），这是否意味着不需要任何土方运输，无论是运出或运入现场？

解决方案

不。任何土壤科学家都会热心地指出，土壤类型会随着位置迅速变化，具体取决于区域。因此，如果一条高速公路的一半从地面开挖，而另一半需要填筑，则不能简单地将从第一半开挖的土方倾倒到第二半，即使在数学上它们是平衡的。如果土壤类型不同，则所需的具体体积可能也不同，因为不同的土壤类型具有不同的性质（沉降，储水等）。在最糟糕的情况下，不咨询土壤科学家可能会导致您的道路被冲毁！