交通运输/交通流基础

葡萄牙的交通拥堵

交通流是研究单个驾驶员和车辆在两点之间移动以及他们相互之间相互作用的学科。不幸的是，研究交通流很困难，因为驾驶员行为无法百分之百确定地预测。幸运的是，驾驶员往往在合理一致的范围内表现；因此，交通流往往具有一定的合理一致性，并且可以粗略地用数学表示。为了更好地表示交通流，已经建立了三个主要特征之间的关系：（1）流量，（2）密度和（3）速度。这些关系有助于道路设施的规划、设计和运营。

交通流理论

时空图

显示车辆随时间和空间变化轨迹的时空图

交通工程师用时空图来表示特定时间特定车辆的位置。这个二维图显示了车辆从特定起点到特定终点的移动轨迹。该图可以表示多辆车，因此可以确定某些特征，例如在特定时间特定地点的流量。

流量和密度

流量 (q) = 车辆通过固定点（车辆数/小时）的速率，$t_{measured}$ = 平均测量时间间距

$q={\frac {3600N}{t_{measured}}}\,\!$

密度（浓度）(k) = 一段路段 (L) 上的车辆数 (N)（单位为车辆数/公里）

$k={\frac {N}{L}}\,\!$

其中

• $N$ = 占用长度为 $L$ 的公路段的车辆数
• $q$ = 等效每小时流量
• $L$ = 道路长度
• $k$ = 密度

速度

测量交通速度并不像看起来那么简单；我们可以对一段时间或空间内单个车辆的速度测量进行平均，而每种方法都会产生略微不同的结果。

时间平均速度

时间平均速度 (${\overline {v_{t}}}\,\!$) = 通过某一点的车辆速度的算术平均值

${\overline {v_{t}}}={\frac {1}{N}}\sum \limits _{n=1}^{N}{v_{n}}\,\!$

空间平均速度

空间平均速度 (${\overline {v_{s}}}\,\!$) 被定义为一段时间内通过某一点的速度的调和平均值。它也等于一段路段上的平均速度。

${\overline {v_{s}}}={\frac {N}{\sum \limits _{n=1}^{N}{\frac {1}{v_{n}}}}}\,\!$

时间平均速度和空间平均速度的关系

请注意，时间平均速度是指通过某一点的平均速度，不同于空间平均速度，后者是指沿一段长度的平均速度。

两种速度之间的关系如下：

${\overline {v_{t}}}={\overline {v_{s}}}+{\frac {\sigma _{s}^{2}}{\overline {v_{s}}}}\,\!$

时间平均速度高于空间平均速度，但二者之间的差异会随着车辆速度可变性的程度而变化。在高速（自由流动）状态下，差异很小，而在拥堵情况下，二者之间的差异可能达到两倍。

间距

以下定义给出了所谓的brutto间隙（Asela）（意大利语，意思是“总的”），与之相对的是netto间隙（意大利语，意思是“净的”）。Netto间隙指的是车辆后保险杠与下一辆车前保险杠之间的距离或时间。

时间间距

时间间距 ($h_{t}\,\!$) = 一辆车的车头到达高速公路上某一点的时间与下一辆车的车头到达同一点的时间之间的差值（以秒为单位）。

平均时间间距 (${\overline {h_{t}}}\,\!$) = 每单位距离的平均行驶时间 * 平均空间间距

${\overline {h_{t}}}={\overline {t}}*{\overline {h_{s}}}\,\!$

空间间距

空间间距 ($h_{s}$) = 一辆车的车头与下一辆车的车头之间的位置差（以米为单位）。

平均空间间距 (${\overline {h_{s}}}\,\!$)= 空间平均速度 * 平均时间间距

${\overline {h_{s}}}={\overline {v_{s}}}*{\overline {h_{t}}}\,\!$

请注意，密度和空间车头间距是相关的。

$k={\frac {1}{\overline {h_{s}}}}\,\!$

交通流量的基本图

传统的交通流量基本图

2000年11月1日在明尼阿波利斯第49/53大道I-94检测器688上，流量随密度变化

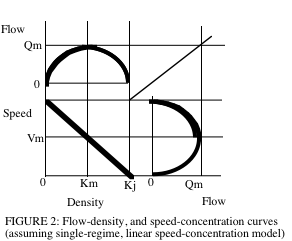
流量、密度和空间平均速度这三个变量在定义上是相关的，如

$q=k{\overline {v_{s}}}\,\!$

传统模型（抛物线型）

传统基本图的属性。

• 当高速公路上的密度为零时，流量也为零，因为高速公路上没有车辆。
• 随着密度的增加，流量也增加。
• 当密度达到最大拥堵密度 ($k_{j}$) 时，流量必须为零，因为车辆将首尾相连排成一行。
• 流量也会增加到最大值 ($q_{m}$)，超过该点的密度增加会导致流量减少。
• 速度是空间平均速度。
• 当密度 = 0 时，速度是自由流动速度 ($v_{f}$)。流量曲线的上半部分是不拥挤的，下半部分是拥挤的。
• 流量密度曲线的斜率表示速度。上升/下降 = 流量/密度 = 每小时车辆数/每公里车辆数 = 公里/小时。

观察结果（三角形或截断三角形）

实际交通数据通常比理想模型所建议的要嘈杂得多。然而，我们往往看到的是，随着密度的增加，速度保持不变到一定程度（容量），然后如果受到下游交通的影响（排队溢出）就开始下降。对于单个路段而言，流量和密度之间的关系因此更接近三角形而不是抛物线。当我们将多个路段汇总在一起（例如，网络）时，我们会看到更接近抛物线的形状。

微观模型和宏观模型

描述交通流量的模型可以分为两类：微观模型和宏观模型。理想情况下，宏观模型是微观模型中所见行为的集合。

微观基本图（截断三角形）中的交通阶段

排队累积输入-输出（Newell）图中的交通阶段

微观模型

微观模型预测汽车的以下行为（速度和位置的变化）作为领先车辆行为的函数。

宏观模型

宏观交通流量理论将交通流量、行驶速度和密度联系起来。将交通流量比作河流，它主要是在有限通道道路上发展起来的（Leutzbach 1988）。基本关系“q=kv”（流量 (q) 等于密度 (k) 乘以速度 (v)）由基本图说明。许多实证研究量化了组成成分的双变量关系（q 与 v、q 与 k、k 与 v），改进参数估计和函数形式（Gerlough 和 Huber 1975、Pensaud 和 Hurdle 1991；Ross 1991；Hall、Hurdle 和 Banks 1992；Banks 1992；Gilchrist 和 Hall 1992；Disbro 和 Frame 1992）。

最常用的模型是 Greenshields 模型，它假设速度和密度之间的关系是线性的。在高性能计算机出现之前，这些模型是最合适的，当时高性能计算机使得使用微观模型成为可能。宏观属性（如流量和密度）是单个（微观）决策的产物。然而，这些微观决策者会受到周围环境的影响，即交通的宏观属性。

虽然交通流量理论家将交通流量表示为流体，但排队分析本质上将交通流量视为一组离散粒子。这两种表示并不一定是矛盾的。右侧的图形显示了基本图和排队输入-输出图中的相同 4 个阶段。这将在下一节中详细讨论，请参见 下一节。

示例

示例 1：时间平均速度和空间平均速度

T问题

问题

给定五个观察到的速度（50 公里/小时、35 公里/小时、45 公里/小时、20 公里/小时和 50 公里/小时），时间平均速度和空间平均速度是多少？

示例

解决方案

时间平均速度

${\overline {v_{t}}}={\frac {1}{5}}(60+35+45+20+50)=42\,\!$

时均速度

${\overline {v_{s}}}={\frac {N}{\sum \limits _{n=1}^{N}{\frac {1}{v_{n}}}}}={\frac {5}{{\frac {1}{60}}+{\frac {1}{35}}+{\frac {1}{45}}+{\frac {1}{20}}+{\frac {1}{50}}}}=36.37\,\!$

时均速度为 42 公里/小时，空均速度为 36.37 公里/小时。

示例 2：计算交通流量特征

T问题

问题

已知 40 辆车在 1 分钟内经过某一点，并行驶了 1 公里，请问流量、密度和时间间隔分别为多少？

示例

解决方案

计算流量和密度

$q={\frac {3600(40)}{60s}}=2400veh/hr\,\!$

$k={\frac {40}{1}}=40veh/km\,\!$

查找空均速度

$q=k{\overline {v_{s}}}=2400=40{\overline {v_{s}}}\,\!$

${\overline {v_{s}}}=60km/hr\,\!$

计算空间间隔

$k=40={\frac {1}{\overline {h_{s}}}}\,\!$

${\overline {h_{s}}}=0.025km=25m\,\!$

计算时间间隔

${\overline {h_{s}}}={\overline {v_{s}}}*{\overline {h_{t}}}=25=(60*1000/3600){\overline {h_{t}}}\,\!$

${\overline {h_{t}}}=1.5s\,\!$

时间间隔为 1.5 秒。

示例 3：在某路段观察到的点速度（单位：公里/小时）分别为 66、62、45、79、32、51、56、60、53 和 49。中位速度（单位：公里/小时）为 。

解决方案：中位速度是在一系列按升序排列的瞬时速度中位于中间值的速率。50% 的速度值将大于中位数，50% 的速度值将小于中位数。瞬时速度研究的升序排列为 32、39、45、51、53、56、60、62、66、79。

中位速度 = (53 + 56) / 2 = 54.5 公里/小时。

思考问题

问题

微观交通流模拟单个车辆的行为，而宏观交通流模拟整个交通流的行为。从概念上讲，微观交通流似乎更准确，因为它基于驾驶员行为而不是简单的流量特征。假设微观模拟可以校准以真正解释驾驶员行为，那么模拟大型网络的主要缺点是什么？

解决方案

计算能力。要使用微观模拟来模拟非常大的网络，需要评估的车辆数量非常大，需要大量的计算机内存。目前，计算机在及时完成非常大的微观网络方面存在问题，但未来可能会有所突破，从而解决这个问题。

示例问题

• 问题 (解决方案)

变量

• $d_{n}$= 第 n 辆车的距离
• $t_{n}$= 第 n 辆车的行驶时间
• $v_{n}$= 第 n 辆车的速度（速度）
• $h_{t,nm}$= 第 n 辆车和第 m 辆车之间的时间间隔
• $h_{s,nm}$ = 第 n 辆车和第 m 辆车之间的空间（距离）间隔
• $q$ = 经过固定点的流量（每小时车辆数）
• $N$ = 车辆数量
• $t_{measured}$ = 测量持续时间（秒数）
• $t$= 行驶时间
• $k$= 密度（每公里车辆数）
• $L$= 道路路段长度（公里）
• $v_{t}$= 时间平均速度
• $v_{s}$= 空间平均速度
• $v_{f}$= 自由流速度（无拥堵速度）
• $k_{j}$= 拥堵密度
• $q_{m}$= 最大流量

关键词

• 时空图
• 流量，速度，密度
• 车头间距（空间和时间）
• 空间平均速度，时间平均速度
• 微观，宏观

补充阅读

• 交通流理论修订专著

视频

• 交通流

参考文献

• Banks, J.H. (1991). 高速公路瓶颈处的两种容量现象：匝道控制的基础？交通研究记录 1320, pp. 83–90.
• Banks, James H. (1992). “高速公路速度-流量-浓度关系：更多证据和解释”。交通研究记录 1225:53-60.
• Cassidy, M.J. 和 R.L. Bertini (1999) 高速公路瓶颈处的一些交通特征。交通研究第 B 部分 第 33 卷, pp. 25–42
• Disbro, John E. 和 Frame, Michael. (1992). “交通流理论和混沌行为”。交通研究记录. 1225: 109-115.
• Gerlough, Daniel L. 和 Huber, Matthew J. (1975). 交通流理论：TRB 特别报告 165. 交通研究委员会，华盛顿特区。
• Gilchrist, Robert S. 和 Fred L. Hall. (1992). “交通流理论变量的三维关系”。交通研究记录. 1225:99-108.
• Hall, F.L. 和 K. Agyemang-Duah (1991). 高速公路容量下降和容量定义。交通研究记录 1320, pp. 91–98
• Hall, Fred L.，Hurdle, V. F. 和 Banks, James H. (1992). “关于高速公路速度-流量和流量-占用（或密度）关系的最新研究综述”。在 TRB 第 71 届年会上发表，华盛顿特区。
• Knoop, V.L.，Hoogendoorn, S.P. 和 Van Zuylen, H.J. (2009) 时间平均速度和空间平均速度之间的经验差异。在 Appert-Rolland, C.，Chevoir, F.，Gondret, P.，Lassarre, S.，Lebacque, J.-P. 和 Schreckenberg, M.（编辑）交通和颗粒流 07 会议论文集。第 351-356 页，施普林格，纽约
• Pensaud, B.N. 和 Hurdle, V. F. (1991). “一些挑战关于速度-流量关系的旧观念的新数据”。交通研究记录. 1194: 191-8.
• Ross, Paul. (1991). “宏观交通模型的一些属性”。交通研究记录. 1194: 129-34.