小学几何/变换
变换是指我们改变图形的大小、方向和/或位置。请注意,变换通常在方格纸上完成,以避免过多的测量并确保准确性。

反射是指图形沿轴反射,形成一个反射对称图形。反射轴也是新图形的对称轴。
看右边图。假设你只被给了左边部分。如何反射图形?首先,找出A点和轴之间的距离。是四格。然后找到A′(读作“A撇”),它应该与轴距离相同,但在轴的另一侧。看看图形右边。如果你找到了那个点,你就对了。在那儿画一个小十字 - 如果你的老师不允许你这样做,就稍后擦掉它!现在对另外两点做同样的事情。把它们连接起来。现在你就形成了反射后的图形!
反射图形时的一个常见错误是忘记标记点。这会导致你损失很多分数,所以不要犯这个错误!此外,永远不要错误地标记点。记住要添加“′”符号,并检查点是否对应!
旋转是最难的一种变换。它需要参考一个点旋转图形。因此,在这个阶段,你只会要求旋转90°、180°和270°。(360°没有意义,但如果你真的碰巧遇到它,你非常幸运!)在旋转图形之前,我们需要注意三件事。
- 旋转的度数
- 你应该顺时针还是逆时针旋转
- 旋转中心在哪里
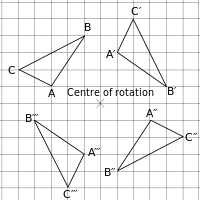
让我们看看左边的例子。假设我们只被给了上面的左边部分。我们需要用不同的方法旋转它。
- 绕中间点逆时针旋转90°
- 绕中间点逆时针旋转180°
- 绕中间点逆时针旋转270°
- 绕中间点顺时针旋转90°
- 绕中间点顺时针旋转180°
- 绕中间点顺时针旋转270°
看看#1和#6。如果你仔细观察,你会发现#1和#6实际上是一样的!可以通过这个例子来解释。要将三角形ABC绕中间点逆时针旋转90°,我们可以先使用点A。点A位于旋转中心的左边三格,上面一格,所以我们可以将它旋转90度。这无法用语言解释,所以试着看看右边图。正如你所看到的,A和A′与旋转中心距离相同。我们对另外两点做同样的事情,产生一个看起来像图中三角形的三角形。如果我们对第6个点做同样的事情,你将产生一个相同的三角形!第3个和第4个点也是一样的。
那么2和5呢?正如我们所看到的,它们都涉及旋转180°;然而,一个是顺时针,另一个是逆时针。让我们先尝试顺时针旋转它。你应该得到图中的三角形A′′B′′C′′。然后对逆时针方向做同样的事情。它们看起来一样吗?
既然我们已经尝试从一个旋转中心旋转了6种可能性,并且发现只有三种,你能尝试将三角形ABC绕点A旋转吗?如果你正在阅读电子书,请在方格纸上复制三角形ABC。如果你使用的是印刷版本,你可以直接在书上画新三角形。将你的新三角形命名为DEF。
平移是一种简单的变换。简单来说,平移是指改变图形的位置。例如,如果我们想将图形向左平移五格,我们只需将它向左移动五格。
平移的过程非常简单。假设我们在方格纸上有一个直角三角形ABC。我们的任务是将其向上平移四格,向左平移两格。我们将直角顶点,命名为A,作为我们的点,将其向上平移四格,然后向左平移两格。在那里画一个小十字,并标记为A′。现在我们参考原始图形重新创建图形。记住要正确命名点。
我们经常被要求追溯在给定平移中发生的平移。我们会得到原始图形和新图形。当处理这种类型的问题时,使用一个点可能会有所帮助,就像我们上面所做的那样。取同一个直角三角形。我们看到A被向上平移了四格。所以我们写道:将A向上平移四格。然后我们看到A向左平移了两格,所以我们写道,然后将A向左平移两格。然后我们就完成了问题!
下表显示了进行变换时会发生哪些变化。
| 变换类型 | 大小 | 形状 | 方向(方向) | 位置 |
|---|---|---|---|---|
| 反射 | 从不 | 从不 | 总是 | 有时 |
| 旋转 | 从不 | 从不 | 总是 | 有时 |
| 平移 | 从不 | 从不 | 从不 | 总是 |
| 放大(缩放) | 总是 | 从不 | 从不 | 有时 |
| 缩小(缩放) | 总是 | 从不 | 从不 | 有时 |
注意:对于所有这些变化,形状永远不会改变。三角形永远是三角形,矩形永远是矩形。
