HSC 扩展 1 和 2 数学/3-单元/预备/参数方程

曲线的参数形式是一种代数表示，它将曲线上的每个点的坐标表示为一个引入的参数的函数，最常见的是 $t$。这与笛卡尔形式形成对比，参数方程没有描述 $x$ 和 $y$ 之间的明确关系。必须推导出这种关系才能从参数形式转换为笛卡尔形式。

在 3-单元中，参数方程侧重于二次函数的参数表示，从参数形式转换为笛卡尔形式，反之亦然，并使用参数方程操作二次函数的几何方面。识别其他参数形式也很有用，更多形式将在 4-单元主题中引入和处理，圆锥曲线.

使用参数形式的原因

在特定情况下（在学校教学大纲中，主要是 圆锥曲线），参数表示可能是有用的，因为

• 曲线上的点由一个数字而不是两个数字表示，简化了代数；
• 一些优雅的结果是可能的；例如，在二次函数的标准参数化中，梯度等于参数，$t$；
• 一些无法用函数形式表示的曲线（例如圆，既不是 $x$ 的函数，也不是 $y$ 的函数）可以用参数形式方便地表示；
• 从直观上讲，它提供了一种更简单的方法来找到图上的点：你可以代入参数的任何值，并立即找到一个点，而关系形式并非以相同的方式确定性。

此外，参数形式出现在某些自然现象中。例如，使用运动方程，可以用抛射运动定律计算抛出球在任何时间的位置。这隐含地通过时间对球的路径进行参数化；为了找到球路径的形状（我们知道它是一个抛物线），我们必须使用参数方程，从方程中消除时间，$t$。

将参数方程转换为笛卡尔方程

最简单的参数形式之一是直线

${\begin{aligned}x&=t\\y&=t\end{aligned}}$

通过观察，很明显这描述了直线 $y=x$。但是，正式执行此操作的方法是什么？

我们正在寻找 $x$ 和 $y$ 之间的某种关系，其中没有 $t$ 。换句话说，我们想要消去方程中的 $t$ 。在上面的例子中，我们通过将第一个和第二个方程相等来消除 $t$ 。

另一个例子

${\begin{aligned}x&=3t+1\\y&=9t^{2}-1\end{aligned}}$

我们解第一个方程得到t，并代入第二个方程

${\begin{aligned}x&=3t+1\\t&={\frac {x-1}{3}}\end{aligned}}$

代入第二个方程

${\begin{aligned}y&=9t^{2}-1\\&=9\left({\frac {x-1}{3}}\right)^{2}-1\\&=x^{2}-2x+1-1\\&=x^{2}-2x\end{aligned}}$

这里我们得到了一个笛卡尔形式，如所要求的那样。

三种标准参数形式

这些参数形式经常出现，三单元和四单元的学生应该认识它们。

抛物线

抛物线的标准参数化描述了一个焦距为 $a\,$ 且顶点在原点的抛物线。在笛卡尔形式中，它表示为

$x^{2}=4ay\,$

在参数形式中，它表示为

${\begin{aligned}x&=2at\\y&=at^{2}\end{aligned}}$

消去 $t\,$ 可以验证它等效于笛卡尔形式

${\begin{aligned}x&=2at\\x^{2}&=4a^{2}t^{2}\\&=4a(at^{2})\\&=4ay\end{aligned}}$

如需。

圆

圆的图示，指示参数的几何意义

半径为 $r\,$ 且圆心位于原点的圆可以用笛卡尔坐标系表示为

$x^{2}+y^{2}=r^{2}\,$

引入参数 $\theta \,$，它就是

${\begin{aligned}x&=r\cos \theta \\y&=r\sin \theta \end{aligned}}$

我们转换为笛卡尔坐标系如下

${\begin{aligned}x^{2}&=r^{2}\cos ^{2}\theta \\y^{2}&=r^{2}\sin ^{2}\theta \\x^{2}+y^{2}&=r^{2}\cos ^{2}\theta +r^{2}\sin ^{2}\theta \\&=r^{2}(\cos ^{2}\theta +\sin ^{2}\theta )\end{aligned}}$

回顾三角恒等式，

$\sin ^{2}\theta +\cos ^{2}\theta =1\,$

我们得出结论

$x^{2}+y^{2}=r^{2}\,$

如需。

几何解释

与大多数参数方程不同，圆锥曲线由 $\theta \,$ 而不是 $t\,$ 参数化。对于圆来说，这意味着一种几何表示：$\theta \,$ 代表该点与 $x$ 轴的夹角。

椭圆

从概念上讲，椭圆只是一个“压扁”的圆。参数形式清楚地表明了这一点。

${\begin{aligned}x&=a\cos \theta \\y&=b\sin \theta \end{aligned}}$

余弦和正弦仍然存在，但现在它们被乘以了 *不同的* 常数，以便$x$ 和 $y$ 分量以不同的方式拉伸。我们可以以类似于圆形的方式将其转换为参数形式。

${\begin{aligned}x^{2}&=a^{2}\cos ^{2}\theta \\y^{2}&=b^{2}\sin ^{2}\theta \\{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}&=\cos ^{2}\theta +\sin ^{2}\theta \\&=1\end{aligned}}$

这是椭圆的标准形式，其中 $x$ 和 $y$ 截距分别为 $\pm a\,$ 和 $\pm b\,$。

抛物线的性质

3-Unit 的学生应该记住抛物线的参数描述 ($x=2at,y=at^{2}$)。他们也应该知道（或者能够快速推导出）抛物线上点 $t$ 和点 $(x_{1},y_{1})$ 的切线和法线方程。

切线和法线方程的推导

对每个参数方程关于 $t\,$ 求导数，

${\begin{aligned}{\frac {dy}{dt}}&=2at\\{\frac {dx}{dt}}&=2a\end{aligned}}$

那么，梯度 ${\tfrac {dy}{dx}}$ 可以通过将 ${\tfrac {dy}{dt}}$ 除以 ${\tfrac {dx}{dt}}$ 获得（这是链式法则）。

${\begin{aligned}{\frac {dy}{dx}}&={\frac {dy}{dt}}{\frac {dt}{dx}}\\&={\frac {2at}{1}}{\frac {1}{2a}}\\&=t\end{aligned}}$

请注意，此结果无需链式法则即可得出，只需对笛卡尔形式（相对于 $x\,$）求导，并解出 $t\,$。然而，以上推导更快更优雅。

点 *P* 处的切线方程

抛物线的示意图，显示了点 *P* 处的法线和切线

点 $P(2at,at^{2})$ 处的切线的斜率为 $t$。点 $P$ 处的切线方程为

使用点斜式公式 $y-y_{1}=m(x-x_{1})\,$，方程为

${\begin{aligned}y-at^{2}&=t(x-2at)\\&=tx-2at^{2}\\y+at^{2}&=tx\\y-tx+at^{2}&=0&{\mbox{ or }}y=xt-at^{2}\end{aligned}}$

点 *P* 处的法线方程

点 $P$ 处的法线的斜率为 ${\tfrac {-1}{t}}$（因为两条垂直线的斜率 $m_{1}\,$ 和 $m_{2}\,$ 必须满足 $m_{1}m_{2}=-1\,$）。类似于切线方程的推导

${\begin{aligned}y-at^{2}&={\tfrac {-1}{t}}(x-2at)\\&={\tfrac {-x}{t}}+{\tfrac {2at}{t}}\\yt-at^{3}&=-x+2at\\yt+x-at(t^{2}+2)&=0&{\mbox{or }}x+ty=2at+at^{3}\end{aligned}}$

抛物线的弦

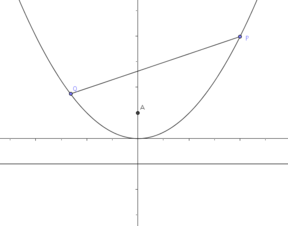抛物线和弦 PQ 的示意图

假设$P(2ap,ap^{2})$ 和 $Q(2aq,aq^{2})$ 是抛物线 $x^{2}=4ay$ 上的两个不同点。我们可以通过求斜率并使用点斜式来推导出直线 $PQ$ 的方程

${\begin{aligned}m&={\frac {ap^{2}-aq^{2}}{2ap-2aq}}\\&={\frac {a(p-q)(p+q)}{2a(p-q)}}\\&={\tfrac {1}{2}}(p+q)\end{aligned}}$

所以弦为

${\begin{aligned}y-ap^{2}&={\tfrac {1}{2}}(p+q)(x-2ap)\\&={\tfrac {1}{2}}(p+q)x-ap^{2}-apq\\y&={\tfrac {1}{2}}(p+q)x-apq\end{aligned}}$

切线的交点

点 $P(2ap,ap^{2})$ 和 $Q(2aq,aq^{2})$ 位于抛物线 $x^{2}=4ay$ 上。点 $P$ 和 $Q$ 处切线的交点可以用 $p$ 和 $q$ 表示。

切线是

${\begin{aligned}y&=px-ap^{2}\\y&=qx-aq^{2}\end{aligned}}$

将两式相减，得

${\begin{aligned}y-y&=px-ap^{2}-(qx-aq^{2})\\0&=px-ap^{2}-qx+aq^{2}\\0&=px-qx+aq^{2}-ap^{2}\\x(p-q)&=a(p^{2}-q^{2})\\x(p-q)&=a(p+q)(p-q)\\x&=a(p+q)\end{aligned}}$

将此结果代入原始的切线公式，得

${\begin{aligned}y&=p(a(p+q))-ap^{2}\\&=ap(p+q)-ap^{2}\\&=ap^{2}+apq-ap^{2}\\&=apq\end{aligned}}$

因此，交点可由 $T(a(p+q),apq)\,$ 描述。