高中化学/原子大小

在元素周期表中，有许多物理性质并不像以前定义的那样“相似”，而是更像趋势。这意味着，当您沿着一组元素或一个周期移动时，您将看到这些性质的趋势变化。我们将讨论三个特定的周期趋势。本章的第一课专门研究元素周期表中原子大小的趋势。接下来的两节课将讨论电离能和电子亲和能。这些趋势都可以用原子的电子构型来理解。

观察到的原子大小的实际趋势与三个因素有关。这些因素是

原子核中质子的数量（称为核电荷）。
容纳电子的能级数量（以及外层能级中电子的数量）。
原子核与其最外层电子之间容纳的电子数量（称为屏蔽效应）。

学习目标

定义原子半径。
说明原子大小的边界问题。
描述测量原子大小的方法。
定义屏蔽效应。
描述决定原子大小趋势的因素。
描述原子大小在族和周期中的总体趋势。
描述元素周期表中各行原子半径的趋势。
描述原子半径趋势如何适用于过渡金属。
使用总体趋势预测原子的相对大小。
使用有效核电荷的概念来解释为什么主族元素的原子半径在元素周期表中向下移动一个族时会增加
由于 f 轨道的复杂结构和 f 电子对的屏蔽效果差，导致镧系收缩现象。

原子没有明确的边界

原子电子云占据的空间区域通常被认为是电子的概率分布，因此，电子云没有明确的“外边缘”。原子大小的定义有几种不同的方式，这些不同的定义通常会产生一些原子大小测量值的变化。

由于从原子核到电子云最外边缘测量原子大小非常困难，化学家使用其他方法来获得一致的原子大小测量值。化学家定义原子大小的一种方法是使用原子半径。原子半径是指双原子分子（双原子分子是指由两个原子组成的分子，同核分子是指两个原子都是相同的元素）中心之间的距离的一半。下图表示原子大小定义的可视化表示。

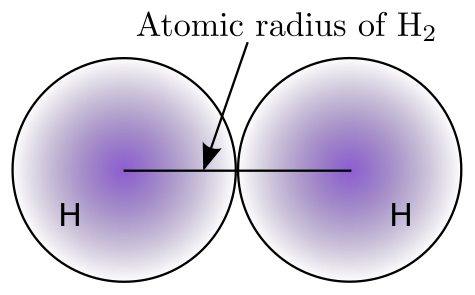
我们如何测量原子的尺寸？卢瑟福因其用α粒子轰击金箔的实验而闻名。卢瑟福在1911年首次进行的金箔实验，在这一单元中对我们特别重要，因为它第一次为科学提供了原子大小的近似测量值。他利用 1900 年代初期的技术，能够定量地确定原子核的近似尺寸为 4×10⁻¹² cm。原子的尺寸略大，直径约为 2×10⁻⁸ cm。

原子大小在同一族中从上到下增加

现在让我们从一个族或族（从上到下）来看原子半径或原子的尺寸。例如，让我们看一下第 1 族金属。这个族（以及所有其他主族）中的每个原子在外层能级中具有与该族中所有其他原子相同的电子数。元素周期表中的每一行（周期）表示另一个添加的能级。当我们第一次学习主能级时，我们了解到每个新的能级都比之前的能级更大。能级 2 比能级 1 大，能级 3 比能级 2 大，等等。因此，当我们从元素周期表中的一周期向下移动到另一周期时，每个连续的周期表示添加了更大的能级。很明显，当我们从元素族向下移动时，每个新原子都添加了一个能级，因此会更大。

影响原子大小的另一个因素是屏蔽效应。原子核中的质子由于静电荷相反，会吸引外层能级中的价电子。这种吸引力的强度取决于电荷的大小、电荷之间的距离，以及原子核和价电子之间的电子数。核心电子屏蔽价电子免受原子核的影响。核心电子的存在削弱了原子核和价电子之间的吸引力。这种吸引力的减弱称为屏蔽效应。屏蔽的程度取决于原子核和价电子之间的电子数。原子核对价电子的吸引力越强，当吸引力强时，价电子层可以收缩得更紧密，而当吸引力减弱时，价电子层不会收缩得那么紧密。屏蔽作用越强，价电子层可以扩展得越远。

表 10.1
元素	质子数	电子构型	能级数
Li	3	[Ne]2s¹	2
Na	11	[He]3s¹	3
K	19	[Ar]4s¹	4
Rb	37	[Kr] 5s¹	5
Cs	55	[Xe]6s¹	6

例如，如果您正在观察钠元素，它的电子构型为

Na: 1s²2s²2p⁶3s¹

外层能级为n = 3，有一个价电子，但这个单个价电子与具有 11 个质子的原子核之间的吸引力被另外 10 个内部（或核心）电子屏蔽了。

当我们将钠原子与铯原子进行比较时，我们注意到质子数和被电子占据的能级数都在增加。原子核和外层电子之间还有更多的电子，从而屏蔽了原子核的吸引力。

Cs: 1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s²4d¹⁰5p⁶6s¹

因此，最外层的电子 6s¹ 被非常松散地束缚。换句话说，由于屏蔽作用，原子核对这个 6s¹ 电子的控制力比它对 3s¹ 电子的控制力弱。所有这一切的结果是原子的大小会更大。表 10.2 给出了第 1 族金属的原子半径值，以及一个可视化表示，以更好地了解元素周期表中一个族中原子大小的变化（原子半径的测量单位为皮米 [pm] 或 1×10⁻¹² 米）。

表 10.2：第 1 族金属的原子半径值
元素	原子半径	视觉
Li	123 pm
Na	157 pm
K	203 pm
Rb	216 pm
Cs	235 pm

对于第 1 族金属而言，元素周期表中所有族或家族都是如此。当您沿元素周期表中的一个族向下移动时，原子的尺寸会增加。例如，卤族中最大的原子是溴和碘（因为砹具有放射性，并且仅存在很短时间，所以我们将它排除在讨论之外）。

示例问题

以下哪一个更大？解释。

(a) As 或 Sb

(b) Ca 或 Be

(c) Po 或 S

解决方案:

(a) Sb，因为它在第 15 族中位于 As 之下。

(b) Ca，因为它在第 2 族中位于 Be 之下。

(c) Po，因为它在第 16 族中位于 S 之下。

如前所述，对于主族金属而言，电子构型中的最外层能级由周期数表示。因此，镁元素 (Z = 12) 位于周期 3，第 2 族。据此，我们可以说有 3 个能级，最外层能级中有 2 个电子。让我们看一下镁的电子构型。

Mg: 1s²2s²2p⁶3s²

从镁移动到锶，锶位于周期 5 的第 2 族。这意味着最外层能级中有两个电子。锶的电子也占据了五个能级。

Sr: 11s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s²

您可以想象，随着能级数的增加，原子的尺寸也会增加。电子云中能级数的增加占据了更多的空间。

因此，元素周期表中一个族或家族内的趋势是，原子尺寸随着能级数的增加而增加。下面的元素周期表显示了原子大小在族中的趋势。箭头表示增加的方向。

原子大小在同一周期中从左到右减小

为了确定周期的趋势，我们需要观察质子数（**核电荷**）、能级数和屏蔽效应。对于元素周期表中的一行，原子序数仍然增加（正如它在族中所做的那样），因此质子数会增加。当我们检查第二周期的能级时，我们发现最外层的能级在电子数增加时不会发生变化。在第二周期中，每个额外的电子都进入第二能级。所以能级数*不会增加*。当我们从左到右穿过一个周期时，最外层能级中的电子数增加*但它仍然是同一个最外层能级*。表 10.3 显示了第二周期元素的电子构型。

表 10.3：第二周期元素的电子构型
元素	质子数	电子构型
锂 (Li)	3	1s²2s¹
铍 (Be)	4	1s²2s²
硼 (B)	5	1s²2s²2p¹
碳 (C)	6	1s²2s²2p²
氮 (N)	7	1s²2s²2p³
氧 (O)	8	1s²2s²2p⁴
氟 (F)	9	1s²2s²2p⁵

观察第二周期元素，质子数从锂（3 个质子）增加到氟（9 个质子）。因此，核电荷在周期中增加。同时，被电子占据的能级数*保持不变*。最外层能级中的电子数从左到右沿着一个周期增加，但这将如何影响半径？我们知道，第二行中的每一种元素在其内层能级中都有两个电子（2 个核心电子）。核心电子屏蔽了外层电子免受原子核电荷的影响。对于锂，有两个核心电子和一个价电子，因此这两个核心电子将屏蔽那个价电子。在铍中，有 4 个质子被 1s² 电子屏蔽。随着质子数增加吸引着外层电子，而核心电子的屏蔽作用相同，*价电子被拉得更靠近原子核，使原子变小*。

在第 17 族中，该族中的第一个元素是氟。对于氟，有 9 个质子和 9 个电子。电子构型是 1s²2s²2p⁵。然而，与锂和铍一样，核心电子仍然相同，即 1s² 电子。由于质子更多，因此核电荷增加。随着核电荷的增加，质子和外层能级之间的拉力也增加，将外层电子拉向原子核。屏蔽原子核的量没有增加，因为核心电子的数量保持不变（本周期为 1s²）。最终结果是，原子尺寸在横跨该行时*减小*。在表 10.4 中，显示了从锂开始到氟结束的行中原子半径的值，以及一个视觉表示来理解元素周期表中族中尺寸变化。

表 10.4：第二周期原子半径值
元素	原子半径	视觉
Li	123 pm
Be	111 pm
B	86 pm
C	77 pm
N	74 pm
O	73 pm
F	72 pm

让我们将这个新趋势添加到元素周期表中。看下面我们新的“周期趋势表”的图表。在图表中你会注意到，周期的趋势箭头显示原子半径从右到左增加，这与从左到右减小相同。

考虑到关于原子尺寸的所有信息，你会认识到元素周期表中最大的原子位于最左边和最底部，即钫，#87，而最小的原子位于最右边和最顶部，即氦，#2。

在族中向下移动时原子变大的事实可能正是你在阅读本节之前所期望的，但原子在周期中向右移动时变小的这一事实很可能是一个巨大的惊喜。确保你理解这个趋势及其原因。

对于过渡元素，趋势不那么有规律

元素周期表中原子半径的一般趋势与下面图表中发现的趋势相似。原子半径最小的元素位于右上角；原子半径最大的元素位于左下角。

到目前为止，我们只研究了主族金属。让我们看看我们的三个因素，并看看这些因素如何符合过渡金属系列。观察过渡金属的第一行，即 3d 行，表 10.5 显示了该行中 10 个元素中每个元素的质子数。质子数正在增加，因此核电荷正在增加。

表 10.5：金属数据汇总
元素	质子数	电子构型
钪 (Sc)	21	[Ar]3d¹4s²
钛 (Ti)	22	[Ar]3d²4s²
钒 (V)	23	[Ar]3d³4s²
铬 (Cr)	24	[Ar]3d⁵4s¹
锰 (Mn)	25	[Ar]3d⁵4s²
铁 (Fe)	26	[Ar]3d⁶4s²
钴 (Co)	27	[Ar]3d⁷4s²
镍 (Ni)	28	[Ar]3d⁸4s²
铜 (Cu)	29	[Ar]3d¹⁰4s¹
锌 (Zn)	30	[Ar]3d¹⁰4s²

电子数量正在增加，但以一种特殊的方式增加。我们知道，随着电子数量在横跨一个周期时增加，这些电子对原子核的吸引力也更大。但是，对于d电子，存在一些额外的**电子-电子排斥**。看一下表 10.5，注意铬的非寻常电子构型。

在铬中，一个 4s 电子被提升以半填充 3d 亚层，电子-电子排斥力较小，原子尺寸也较小。该行的后半部分正好相反。表 10.6 显示了过渡金属的第一行及其尺寸。

表 10.6：3d 金属的原子半径
元素	原子半径
钪 (Sc)	164 pm
钛 (Ti)	147 pm
钒 (V)	135 pm
铬 (Cr)	129 pm
锰 (Mn)	137 pm
铁 (Fe)	126 pm
钴 (Co)	125 pm
镍 (Ni)	125 pm
铜 (Cu)	128 pm
锌 (Zn)	137 pm

我们可以看到，3d 过渡金属中的趋势不像主族元素那样有规律。

课程总结

原子尺寸是指从原子核到价电子所在的价电子层之间的距离。
原子尺寸很难测量，因为它没有明确的边界。围绕原子核的电子存在于电子云中。你可以预测电子的存在概率，但不能预测其确切位置。
原子尺寸是间接确定的。
原子半径是定义原子尺寸的一种更明确、更可测量的量。它是同核双原子分子中两个原子中心之间的距离。
卢瑟福通过他的金箔实验为确定原子的大小做出了贡献。
有三个因素有助于预测元素周期表中的趋势：原子核中的质子数、电子层数和屏蔽效应。
由于三个因素都增加，原子尺寸在任何族中从上到下增加。（随着能级数的增加，尺寸必须增加。）
横跨一个周期（从左到右），质子数增加，因此核电荷增加。（横跨一个周期，电子能级数保持不变，但这些能级内的电子数增加。因此电子被拉得更靠近原子核。）
屏蔽相对恒定，因为核心电子保持不变。
元素周期表中的趋势是，当您从左到右穿过元素周期表时，原子半径减小。对于过渡金属，这种趋势不那么有规律，因为其他因素起作用。

复习题

为什么原子尺寸被认为是“没有明确的边界”？
原子尺寸是如何测量的？
(a) 使用分光光度计

(b) 使用微型尺（称为纳米尺）

(c) 间接

(d) 直接
画出碘分子原子半径的视觉表示。
以下哪一个更小？
(a) In 或 Ga

(b) K 或 Cs

(c) Te 或 Po
用你自己的话说解释为什么碘比溴大。
哪些三个因素决定了族中原子尺寸的趋势？
哪些族倾向于表现出这种趋势？
以下哪一个具有最大的原子半径？
(a) Si

(b) C

(c) Sn

(d) Pb
以下哪一个具有最小的原子半径？
(a) 2s²

(b) 4s²4p³

(c) 2s²2p⁴

(d) 4s²
按原子半径递增的顺序排列以下元素：Tl、B、Ga、Al、In。
按原子半径递增的顺序排列以下元素：Ge、Sn、C。
以下哪一个更大？
(a) Rb 或 Sn

(b) Ca 或 As
按原子半径递增的顺序排列以下元素：Mg、Cl、S、Na。
描述元素周期表中行的原子尺寸趋势。
绘制元素周期表的视觉表示，描述原子尺寸的趋势。
以下哪一个具有最大的原子半径？
(a) Sr

(b) Sn

(c) Rb

(d) In
以下哪一个具有最小的原子半径？
(a) K

(b) Kr

(c) Ga

(d) Ge
按原子半径递增的顺序排列以下元素：In、Ca、Mg、Sb、Xe。
按原子半径递减的顺序排列以下元素：Al、Ge、Sr、Bi、Cs。
了解行的趋势，你预计原子获得一个电子后对原子半径的影响是什么？用一个例子来解释。
了解行的趋势，你预计原子失去一个电子后对原子半径的影响是什么？用一个例子来解释。

词汇

原子半径: 同核分子中两个原子核心的距离的一半。
原子大小: 原子尺寸是指从原子核到价电子所在的价电子层之间的距离。
电子-电子排斥: 由于电子具有相同的电荷而产生的分离。
核电荷: 原子核中质子的数量。
屏蔽效应: 原子中的内层电子会干扰原子核对最外层电子的吸引。

← 周期表中的趋势 · 电离能 →

本资料改编自可在此处找到的原始 CK-12 书籍。本作品根据知识共享署名-相同方式共享 3.0 美国许可发布。