高中三角函数/实数的圆函数

在本课中，您将以连续的圆函数形式查看围绕坐标网格旋转的角度的三角比。将建立旋转角度增加或减少时比率如何变化以及函数的图形如何描述这种变化之间的联系。

学习目标

将六个基本三角比识别为围绕原点旋转角度的连续函数。
识别六个基本三角函数的定义域和值域。
识别弧度和角度度量，以及单位圆上象限角的坐标，以及参考角为 30°、45° 和 60° 的坐标。

y = sin(x), 正弦图

到目前为止，您已经对围绕坐标网格的某些旋转角度的正弦、余弦和正切的特定值非常熟悉。在数学中，我们经常可以通过观察一个量在另一个量一致变化时如何变化来了解很多。在这种情况下，当我们逐渐绕坐标网格旋转时，例如，角度的正弦值会发生什么变化。我们将正弦值视为围绕坐标网格旋转角度的函数。我们将任何此类函数称为圆函数，因为它们可以使用单位圆来定义。首先，您可能还记得从前面的部分中，坐标网格中标准位置角的正弦是 ${\tfrac {y}{r}}$ 的比率，其中 y 是角度上任何点的 y 坐标，r 是从原点到该点的距离。

由于无论半径 r 的长度如何，给定角度的比率都是相同的，因此我们可以使用单位圆来使事情更方便。

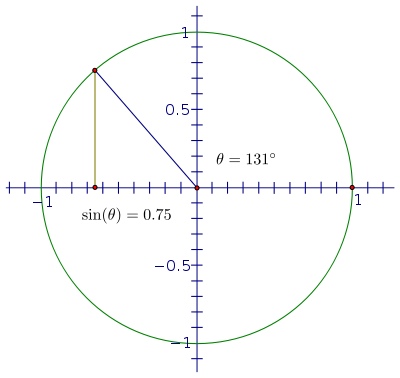
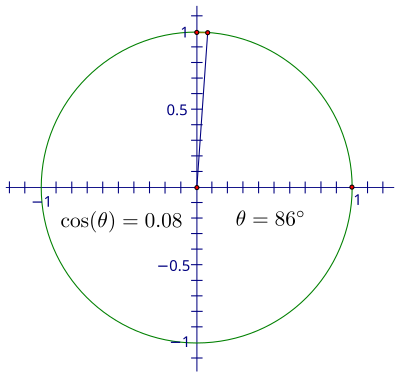
现在分母为 1，所以我们有更简单的表达式 sin(θ) = y。这样做的好处是我们可以使用单位圆上点的 y 坐标来追踪 sin(θ) 的值在整个旋转过程中。想象一下，如果我们从 0 开始，然后逆时针旋转，角度逐渐增大。由于 y 坐标是正弦值，因此请在旋转时观察点的垂直高度。

在第一象限，该高度会变大，从 0 开始，一开始增长很快，然后逐渐变慢，直到角度达到 90°，此时，高度达到最大值 1。

当您旋转到第三象限时，高度的变化现在反转，并开始向 0 减少。

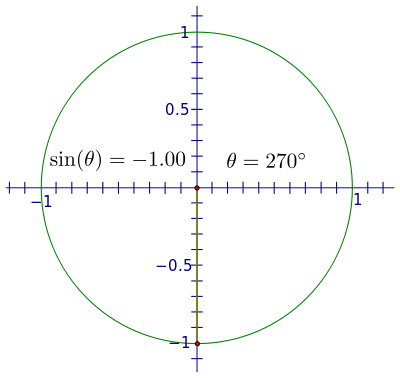
当您开始旋转到第三和第四象限时，线段的长度会增加，但这次是负方向，在 270° 增长到 −1，并在 360° 回到 0。

完成一次旋转后，即使角度继续增加，正弦值也会简单地重复。如果我们选择顺时针旋转来研究负角度，也会发生同样的情况，这解释了为什么正弦函数是周期性的。周期是 2π 弧度或 360°，因为这是角度度量所需的度数，在此之前角度的正弦将简单地重复之前的数值序列。

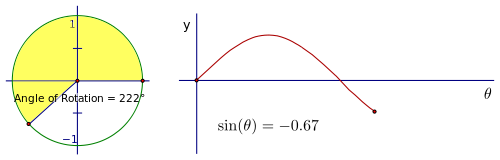
让我们将这种圆周运动转换为正弦值与旋转角度的图形。以下图片序列演示了这种联系。随着旋转角度的增加，观察角度上点的 y 坐标，它水平地进行追踪。此时忽略水平轴上的值，因为它们只是相对的。重要的是您在圆周旋转和点垂直高度的变化之间建立联系。

请注意，一旦我们旋转一圈，该点就会沿着相同的值再次追踪。您看到的红色曲线是正弦“波”的一个周期。下面的动画展示了这种情况在“实时”中的发生。

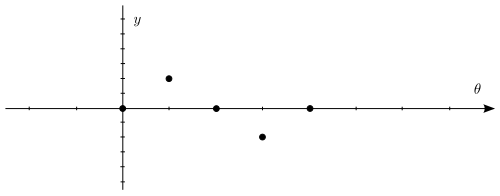
让我们看一些特定值，以便更精确地绘制正弦函数。由于我们已经知道它们之间的变化情况，因此您可以通过绘制象限角（0、 ${\tfrac {\pi }{2}}$ 、π、 ${\tfrac {3\pi }{2}}$ 、2π）的点来绘制一个相当准确的草图。

sin(θ) 的值从 0 到 1 到 0 到 −1 然后再回到 0。沿着显示 θ 的水平轴绘制时，它看起来像这样

填充它们之间的间隙，并允许多次旋转以及负角度，从而得出 y = sin(x) 的图形，其中 x 是任何旋转角度（通常用弧度表示）

正如我们已经提到的，sin(x) 的周期为 2π。您还应该注意，y 值从不超过 1 或低于 −1，因此正弦波的值域为 {−1 ≤ y ≤ 1}。由于我们可以无限期地继续绕圆旋转，因此对角度 x 没有限制，因此 sin(x) 的定义域是所有实数。

y = cos(x), 余弦图

在第 1 章中，您学习了正弦和余弦密切相关。角度的余弦与补角的正弦相同。因此，正弦和余弦波非常相似这一事实应该不会让您感到惊讶，因为它们都是周期性的，周期为 2π，值域从 −1 到 1，定义域是所有实数角度。

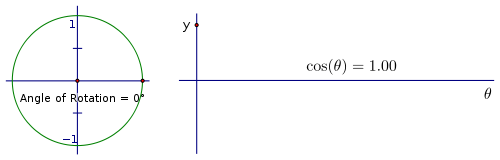
角度的余弦是 ${\tfrac {x}{r}}$ 的比率，因此在单位圆中，余弦是旋转点的 x 坐标。如果我们通过旋转追踪 x−坐标，您会注意到距离的变化类似于 sin(x)，但 cos(x) 从不同的位置开始。0° 角的 x−坐标为 1，90° 的 x 坐标为 0，因此余弦值在第一象限从 1 减少到 0。

这是一个类似于我们用于正弦的旋转序列。这次将旋转点的 x 坐标与它沿着水平线追踪时的点的高度进行比较。

y = cos(x) 的图形的周期为 2π。与 sin(x) 一样，x 值从不“逃离”单位圆，因此它们始终保持在 −1 和 1 之间。余弦波的值域也是 {−1 ≤ y ≤ 1}。并且也与正弦函数一样，对旋转角度没有限制，因此 cos(x) 的定义域是所有实数。

y = tan(x), 正切图

正切比作为旋转角度的函数的图形呈现了一些复杂性。首先，定义域不再是所有实数角度。您可能还记得，对于某些角度（例如，90° 和 270°），正切是未定义的。正如我们将在本节中看到的，tan(x) 的值域实际上是所有实数。

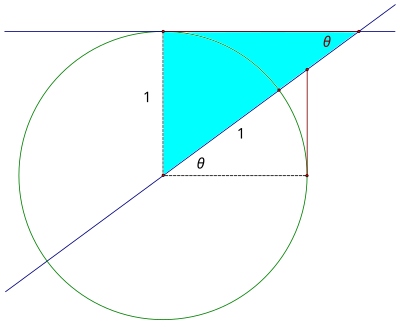
可以使用单位圆上的单一线段来测量六个三角函数中的每一个，但是，其余函数不像正弦和余弦那样明显。正切函数的名称来自正切线，正切线是指与圆的半径垂直于圆上一点的直线，因此该直线仅在一个点上与圆相交。所以，要创建正切线段，我们首先画一条垂直于x轴的正切线。

如果我们将角度θ穿过单位圆，使其与正切线相交，则正切函数定义为红色线段的长度。

虚线段为 1，因为它就是单位圆的半径。回想一下，θ的正切是 ${\tfrac {y}{x}}$ ，因此我们可以使用相似三角形来验证该线段确实是正切。

\tan(\theta )={\frac {y}{x}}={\frac {t}{1}}=t

\tan(\theta )=t\,\!

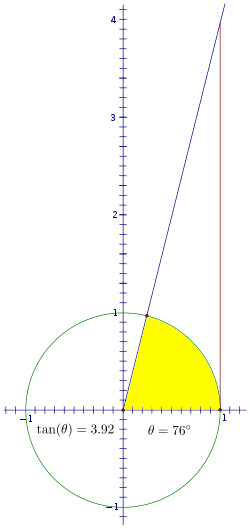
所以，随着我们增加旋转角度，思考一下这个线段是如何变化的。当角度为 0 时，线段没有长度。当我们开始在第一象限旋转时，它会增加，最初会非常缓慢。

但是，你可以很快看到值超过了 1。随着角度越来越接近 90°，线段需要向上延伸很远才能与角度的延伸部分相交，并且它将以越来越快的速度增长。

当我们非常接近y轴时，线段变得无限大，直到角度真正达到 90°，此时角度的延伸部分和正切线将实际平行，因此永远不会相遇！

这意味着正切线段的长度没有定义，或者，可以将其理解为，正切线段无限大。

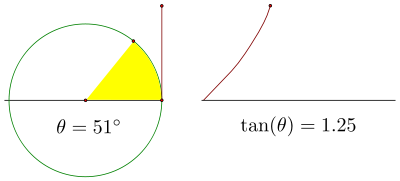
在继续之前，让我们看一下该图形在第一象限的部分。正切从 0 开始，对应 0° 角，然后最初缓慢增加。随着我们接近 90° 旋转，该增量变得更加陡峭。

再次，这些图形中x轴上的一个小间断将更清楚地表明这两个需要注意的概念并排位于同一坐标系中。

事实上，随着我们无限接近 90°，正切值无限制地增加，直到我们真正达到 90°，此时正切是未定义的。图形无限接近但没有接触的直线称为渐近线。因此正切函数在 90° 处有一个渐近线。

当我们旋转超过 90° 时，现在角度的延伸部分和正切线的交点实际上位于x轴下方。这与我们对第二象限角的正切为负的认识非常吻合。它将首先非常负，但随着角度旋转，线段变短，达到 0，然后随着角度进入第三象限，再次回到正数。

随着线段接近 270°，它将再次变得无限大。在 270° 处未定义后，角度进入第四象限，并且再次从无限负值变为接近零，直到我们完成完整的旋转。

所以，这个运动在多个旋转中绘制的图形将如下所示

注意，x轴以弧度（不是以π为单位）测量。我们的渐近线每π弧度出现一次，从 ${\tfrac {\pi }{2}}$ 开始。因此，图形的周期为π弧度。定义域为所有实数，除了 ${\tfrac {\pi }{2}}$ 、 ${\tfrac {3\pi }{2}}$ 、− ${\tfrac {\pi }{2}}$ 等处的“空洞”，值域为所有实数。

三个倒数函数：cot(x)、csc(x) 和 sec(x)

余切

余切是正切的倒数，因此在y轴上的一点画正切线并延长角度（而不是x轴）来生成余切的圆函数是有意义的。

我们可以再次使用相似三角形来验证这一点。因为假定的余切线段平行于黄色三角形的底边，所以角度θ位于对角，三角形确实是相似的，即使它们的位置颠倒。

所以，

\cot(\theta )={\frac {x}{y}}={\frac {t}{1}}=t

\cot(\theta )=t\,\!

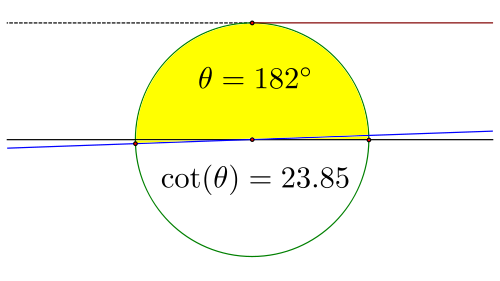
现在我们已经建立了余切线段，思考一下当我们从 0° 开始绕坐标网格旋转时，这条线段是如何变化的。首先，在 0° 本身，余切是未定义的，因为线段平行于角度 θ 的射线。当我们开始增加旋转角度时，线段将变得非常大，并且在我们接近 90° 时开始变小，一开始速度非常快，但随着它越来越接近 90° 时的 0 长度，速度会变慢。

经过 90° 后，线段将再次开始变长，但这次它将在负方向上，一开始缓慢增加，然后在负方向上无限增大，直到 180°，此时它再次变得未定义。

经过这一点后，周期性行为开始出现，当我们从 180° 旋转回 360° 时，该函数现在重复相同的值序列。

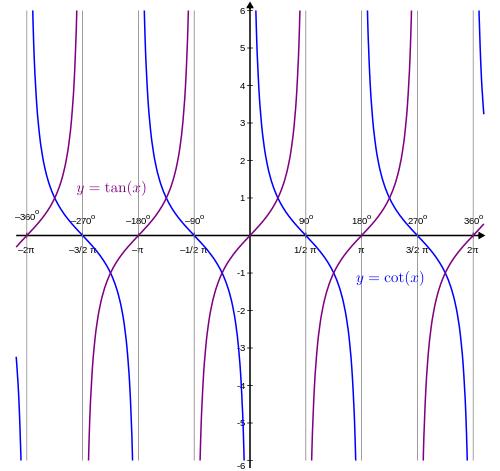
在几个周期内将此运动轨迹绘制在图形上，得到

记住余切和正切互为倒数，因此在正切等于 0 的任何点，余切都将是未定义的，而在正切未定义的任何点，余切等于 0。

您可能还会注意到，这些图形始终在 1 和 -1 处相交。这些是具有 45° 参考角的角度，这些角度的正切和余切总是等于 1 或 -1。一个函数及其倒数是相同的唯一值是 1 和 -1 是有道理的。当我们查看余割和正割与其倒数正弦和余弦的比较时，请记住这一点。

余切函数的定义域是所有实数角度，除了 π 的倍数 {… − 2π. − π.0, π, 2π …}。值域是所有实数。

余割

找到余割线段有很多可能的方法。一种方法是查看由余切线段形成的直角三角形，并使用勾股定理来生成余割。

a^{2}+b^{2}=c^{2}\,\!

1^{2}+\left({\frac {x}{y}}\right)^{2}=c^{2}

\left({\frac {y}{y}}\right)^{2}+\left({\frac {x}{y}}\right)^{2}=c^{2}

{\frac {y^{2}}{y^{2}}}+{\frac {x^{2}}{y^{2}}}=c^{2}

{\frac {y^{2}+x^{2}}{y^{2}}}=c^{2}

从单位圆中的原始三角形，y² + x² = r²

{\frac {r^{2}}{y^{2}}}=c^{2}

\left({\frac {r}{y}}\right)^{2}=c^{2}

由于 ${\tfrac {r}{y}}$ 是余割，则余割必须与边 c 相同。

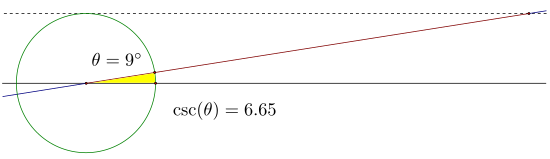
追踪这条线段的长度，它在 0° 时未定义，对于非常小的角度来说是无限大的，在 90° 时减小到 1，然后无限增大，直到在 180° 时未定义。这个过程从 180° 重复到 360°，但是，线段从无限负开始，在 270° 时增加到 -1，然后接近无限负长度。

因此，该函数的周期为 2π，定义域为所有实数角度，除了 π 的倍数 {… −2π, −π, 0, π, 2π …}。值域是所有大于 1 或小于 -1 的实数。

然后图形将如下所示

这是 y = sin(x) 的图形

再次注意 0 处的倒数关系和渐近线。还要注意图形在 1 和 -1 处的交点。许多学生在看到余割图形的一半周期时会想起抛物线。虽然它们在每个都有一个局部最小值或最大值并且它们在相同的方向开始和结束方面相似，但比较到此为止，它们不应被视为抛物线。定义图形值，因此也定义图形形状的数学完全不同于抛物线的二次函数。

正割

与正弦和余弦之间的关系非常相似，正割和余割也有很多相似之处。用于生成 y = sec(x) 的线段如下所示

你将在练习部分演示这一点。这个线段在 0° 时为 1 个单位，然后在第一象限增长，并在 90° 时未定义。它在第二象限无穷地缩小到 −1，然后在第三象限再次向无穷负方向伸长，并在 270° 时未定义。将此运动转换为 y = sec(x) 的图形，得到

将它与余弦图形进行比较

周期为 2π，范围与 y = csc(x) 相同 {y : y ≥ 1 或 y ≤ −1}，定义域为所有实数角度，除了 ${\tfrac {\pi }{2}}$ 的倍数 {… − ${\tfrac {3\pi }{2}}$ , − ${\tfrac {\pi }{2}}$ , ${\tfrac {\pi }{2}}$ , ${\tfrac {3\pi }{2}}$ …}.

课程总结

通过将它们视为绕以原点为中心、半径为一的圆旋转的点 (x, y) 来考虑，可以将定义为直角三角形中比率的六个三角函数置于坐标网格的上下文中。这个圆被称为**单位圆**。旋转角的正弦是点的 y 坐标，旋转角的余弦是 x 坐标，切线是 ${\tfrac {y}{x}}$ 。其他三个比率的值；余切、余割和正割也可以根据它们的倒数关系找到，但所有这些值都可以通过几何方式构造为单位圆上旋转角周围的各种线段。与其找到孤立的值，不如将每个比率视为旋转角的**函数**。这些被称为**圆函数**。以下是六个圆三角函数的定义域和值域。

表 2.3
函数	定义域	值域
sin(x)	所有实数	{y : −1 ≤ y ≤ 1}
cos(x)	所有实数	{y : −1 ≤ y ≤ 1}
tan(x)	{x : x ≠ n · ${\tfrac {\pi }{2}}$ ，其中 n 是任何奇数整数}	所有实数
csc(x)	{x : x ≠ nπ，其中 n 是任何整数}	{y : y > 1 或 y < −1}
sec(x)	{x : x ≠ n · ${\tfrac {\pi }{2}}$ ，其中 n 是任何奇数整数}	{y : y > 1 或 y < −1}
cot(x)	{x : x ≠ n · ${\tfrac {\pi }{2}}$ ，其中 n 是任何奇数整数}	所有实数

复习问题

证明该图中边 A 等于 sec(θ)。
在第 1 章中，你学习了 tan²(θ) + 1 = sec²(θ)。使用该图和问题 1 的结果来证明这个恒等式。
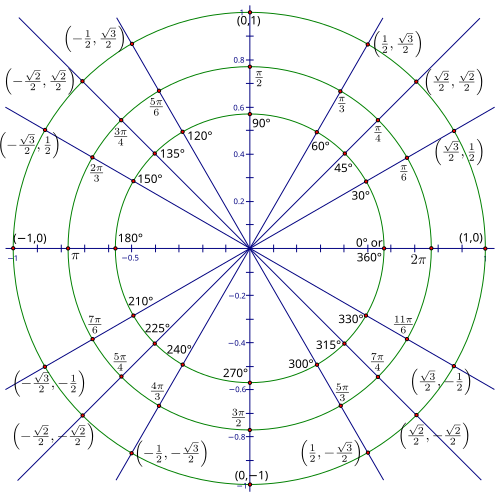
该图显示了单位圆，其中所有角度的参考角为 30°、45° 和 60°，以及象限角。标注单位圆上所有点的坐标。在最小的圆圈上，以度数标注角度，在中间的圆圈上，以弧度标注角度。
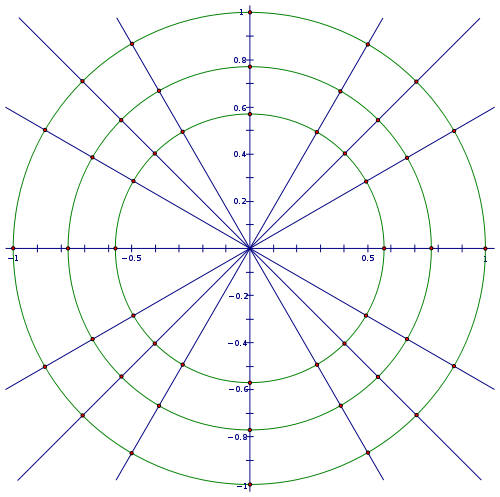
在以下图中绘制并标注表示六个三角函数（正弦、余弦、正切、余割、正割、余切）的线段。
以下哪些选项显示了当 x 从 0 增加到 ${\tfrac {\pi }{2}}$ 时都增加的函数？
(a) sin(x) 和 cos(x)

(b) tan(x) 和 csc(x)

(c) sec(x) 和 cot(x)

(d) csc(x) 和 sec(x)
当 x 从 ${\tfrac {3\pi }{2}}$ 增加到 2π 时，以下哪些陈述是正确的？
(a) cos(x) 趋近于 0

(b) tan(x) 变得无穷大

(c) cos(x) < sin(x)

(d) cot(x) 变得无穷小

复习答案

使用相似三角形

所以

${\frac {x}{1}}=$	${\frac {1}{A}}$
$Ax=\,\!$	$1\,\!$
$A=\,\!$	${\frac {1}{x}}$
$\cos(\theta )=\,\!$	$x\,\!$
${\frac {1}{\cos(\theta )}}=$	${\frac {1}{x}}$
${\frac {1}{\cos(\theta )}}=$	$\sec(\theta )={\frac {1}{x}}$
$\therefore \sec(\theta )=\,\!$	$A\,\!$