高中三角函数/弧度制应用

在本课中，您将把弧度制应用于涉及旋转的各种问题解决情境中。

学习目标

• 使用弧度制解决涉及旋转角度的问题。
• 通过计算弧长来解决问题。
• 通过计算扇形面积来解决问题。
• 根据中心角和半径来近似估计弦长。

旋转

示例 1 时钟的指针显示 11:20。用弧度制将时针和分针形成的钝角表示为最接近的十分之一弧度。 下图显示了指针在指定时间的位置。 解决方案: 由于时钟上有 12 个刻度，每个小时标记之间的角度为 ${\tfrac {2\pi }{12}}$ = ${\tfrac {\pi }{6}}$（或 30°）。因此，12 和 4 之间的角度为 4 · ${\tfrac {\pi }{6}}$ = ${\tfrac {2\pi }{3}}$（或 120°）。由于从 12 到 4 的旋转是完整旋转的三分之一，因此假设时针连续移动，并且已经移动了 11 和 12 之间距离的三分之一，这似乎是合理的。因此，${\tfrac {2}{3}}$ · ${\tfrac {\pi }{6}}$ = ${\tfrac {2\pi }{18}}$，因此角度的总量为 ${\tfrac {2\pi }{18}}$ + ${\tfrac {2\pi }{3}}$ = ${\tfrac {2\pi }{18}}$ + ${\tfrac {12\pi }{18}}$ = ${\tfrac {14\pi }{18}}$。使用计算器近似角度将得到 14π/18 2.44346 最接近的十分之一弧度是 2.4 弧度。

弧长

圆上弧的长度取决于旋转角度和圆的半径长度。如果你还记得上一课的内容，我们将弧度定义为一个角度为θ的弧的长度，以弧度为单位，定义为一个半径长度截取的弧的长度，因此半旋转为 π 弧度，或略大于圆周的 3 个半径长度。如果半径为 4 厘米？半圆弧的长度将为 π 个半径长度，即 4π 厘米。

这得出了一个可以用来计算任何弧长的公式。

$s=r\theta \,\!$

其中s 是弧长，r 是半径，θ 是以弧度为单位的角度。

求解此方程以求θ 将得到一个公式，用于在给定弧长和半径长度的情况下找到弧度量

$\theta ={\frac {s}{r}}$

示例 2 NCAA 篮球场的罚球线宽 12 英尺。在国际比赛中，它只有大约 11.81 英尺。NCAA 球场罚球线上方半圆的长度比国际比赛长多少？ 解决方案: 弧长计算 NCAA 国际 s1 = rθ s2 = rθ s1 = 6(π) s2 ≈ 5.905(π) s1 = 6π s2 ≈ 5.905π 因此答案约为 6π − 5.905π ≈ 0.095π。 .095π .0.29845130209103 这大约是 0.3 英尺，或大约 3.6 英寸。

示例 3 两个连接的齿轮正在旋转。较小的齿轮的半径为 4 英寸，较大的齿轮的半径为 7 英寸。当较小的齿轮完成一次完整旋转时，较大的齿轮旋转的角度是多少？ 解决方案: 由于蓝色齿轮完成一次完整旋转，因此所行进的弧长为 s = rθ s = 4 · 2π 因此，较大切圆上的 8π 弧长将形成以下角度 θ = ${\tfrac {s}{r}}$ θ = ${\tfrac {8\pi }{7}}$ θ ≈ 3.6 所以这个角度大约是3.6弧度。 3.6 · ${\tfrac {180}{\pi }}$ ≈ 206°

扇形面积

最常见的几何公式之一是圆形的面积

$A=\pi r^{2}\,\!$

就角度旋转而言，这是由2π弧度产生的面积。

$2\pi {\text{ radian angle}}=\pi r^{2}{\text{ area}}\,\!$

半圆或π弧度旋转将产生一个圆形的部分，或称为扇形，其面积等于圆形面积的一半，即

${\frac {1}{2}}\pi r^{2}$

因此，1弧度角将定义一个扇形的面积等于

${\frac {2\pi }{2\pi }}=$	${\frac {\pi r^{2}}{2\pi }}$
$1=\,\!$	${\frac {1}{2}}r^{2}$

由此我们可以确定任何角度θ弧度所产生的扇形面积为

$A={\frac {1}{2}}r^{2}\theta$

示例4 作物通常采用中心支点灌溉技术种植，这种技术会形成圆形田地。 以下是堪萨斯州使用这种灌溉系统的田地的卫星图像。 如果灌溉管长度为450米，那么旋转${\tfrac {2\pi }{3}}$弧度后可以灌溉的面积是多少？ 解决方案: 使用公式 $A={\frac {1}{2}}r^{2}\theta$ $A={\frac {1}{2}}(450)^{2}\left({\frac {2\pi }{3}}\right)$ .5*4502*2π/3 212057.5041 该面积约为212,058平方米。

弦长

你可能还记得你在几何学习中，弦是连接圆周上两点的线段。

${\overline {AB}}$是圆形中的弦。

如果我们知道角度和半径的长度，就可以计算出任何弦的长度。因为弦的每个端点都在圆周上，所以从圆心到A和B的距离与半径长度相同。

接下来，如果我们平分这个角，角平分线必须垂直于弦（我们将在几何课上证明这一点）。这就形成一个直角三角形。

现在我们可以使用一个简单的正弦比率来找到弦的一半，这里称为c，然后将结果加倍以找到弦的长度。

$\sin \left({\frac {\theta }{2}}\right)=$	${\frac {c}{r}}$
$c=\,\!$	$r\cdot \sin \left({\frac {\theta }{2}}\right)$

所以弦长为

$2c=2r\sin \left({\frac {\theta }{2}}\right)$

例 5 求半径为 8 厘米，圆心角为 110° 的圆的弦长。将答案四舍五入到最接近的毫米。 解决方案: 先估计答案始终是一个好的问题解决技巧。估计量度的思考过程可能如下所示 角度略大于 90° 或 ${\tfrac {\pi }{2}}$ 弧度。 ${\tfrac {\pi }{2}}$ 弧度略大于 1.5 个半径长度。一个半径是 12，所以我们可能期望答案略大于 12 厘米。让我们看看实际答案与之相比如何。 我们必须首先将角度测量转换为弧度 $100\cdot {\frac {\pi }{180}}={\frac {11\pi }{18}}$ 使用公式，弦长的一半应等于圆的半径乘以角度一半的正弦值。 ${\frac {11\pi }{18}}\cdot {\frac {1}{2}}={\frac {11\pi }{36}}$ 8 · sin $\left({\tfrac {11\pi }{36}}\right)$ （确保你的计算器处于弧度模式！） 将结果乘以 2。 8sin(11π/36) 6.553216354 Ans*2 13.10643271 因此，弧长约为 13.1 厘米。根据我们的估计，这似乎非常合理。

复习题

1. 右边的图像显示了巴西巴拉那州库里提巴的 24 小时制时钟。

   (a) 时钟上每个数字之间的角度用以下方式表示

   i. 用 π 表示的精确弧度量？

   ii. 四舍五入到最接近的十分之一弧度？

   iii. 角度量？

   (b) 估计显示时间时指针之间的角度量

   i. 四舍五入到最接近的整数度

   ii. 用 π 表示的弧度量

2. 

   右边的图片是新泽西州普林斯顿普林斯顿大学校园建筑的窗户。

   (a) 用 π 表示的窗户中央小圆上两个相邻圆点的精确弧度量是多少？

   

   (b) 如果这个圆的半径约为 0.5 米，则每个相邻点中心之间的弧长是多少？将答案四舍五入到最接近的厘米。

   

3. 现在看看窗户中下一个更大的圆。

   

   (a) 找到这个窗户中两个相邻点之间的精确弧度量，用 π 表示。

   (b) 这个窗户玻璃部分的半径约为 1.20 米。计算突出显示的弦长估计值，四舍五入到最接近的厘米。解释你解决方法背后的推理。

   

4. 州冠军赛将在雷·迪亚兹纪念体育馆举行。座位在球场周围形成一个完美的圆圈。阿基米德高中的校长收到了以下图表，显示了分配给学校学生的座位。
   
   从球场中心到看台起点距离为 55 英尺，从球场中心到终点距离为 110 英尺。计算以下各组的近似平方英尺数

   (a) 来自阿基米德的学生

   (b) 普通入场

   (c) 新闻界和官员

5. 

   右边是科罗拉多州旗的图片。事实证明，金色圆圈的直径是 ${\tfrac {1}{3}}$ 国旗的总高度（与黄色条纹的宽度相同），红色圆圈的外径是 ${\tfrac {2}{3}}$ 国旗的总高度。红色条带缺失部分形成的角度为 ${\tfrac {\pi }{4}}$ 弧度。在一面高 33 英寸的旗帜上，红色部分的面积是多少平方英寸（四舍五入到最接近的平方英寸）？

复习答案

1.  

   (a) i. ${\tfrac {\pi }{12}}$

       ii. ≈ 0.3 弧度

       iii. 15°

   (b) i. 20°。答案可能会有所不同，约为 15° 且小于 25° 都是合理的。

       ii. ${\tfrac {\pi }{9}}$。同样，答案可能会有所不同。

2.  

   (a) ${\tfrac {\pi }{6}}$

   (b) ≈ 26 厘米

3.  

   (a) ${\tfrac {\pi }{16}}$

   (b) 为了简化，我们假设弦延伸到每个点的中心。我们需要找到连接这两个点的圆心角的度数。
   
   由于有 13 个点，该角为 ${\tfrac {13\pi }{16}}$。弦的长度则为

   $=2r\sin \left({\frac {\theta }{2}}\right)$

   $=2\cdot 1.2\cdot \sin \left({\frac {1}{2}}\cdot {\frac {13\pi }{16}}\right)$

   2*1.2sin(13π/32)

   2.296656806

   弦的长度大约为 2.30 厘米。

4. 每一段都是 ${\tfrac {\pi }{6}}$ 弧度。因此，看台每一部分的面积为外扇形面积减去内扇形面积

   (a) 学生占有四部分，约为 9,503 平方英尺

   (b) 有三部分为普通入场区，约为 7,127 平方英尺

   (c) 只有一个新闻和官员区，约为 2,376 平方英尺

   $A=A_{\text{outer}}-A_{\text{inner}}\,\!$

   $A={\frac {1}{2}}(r_{\text{outer}})^{2}\cdot {\frac {\pi }{6}}-{\frac {1}{2}}(r_{\text{inner}})^{2}\cdot {\frac {\pi }{6}}$

   $A={\frac {1}{2}}(110)^{2}\cdot {\frac {\pi }{6}}-{\frac {1}{2}}(55)^{2}\cdot {\frac {\pi }{6}}$

   .5*110²*π/6-.5*55²
   *π/6

   2375.829444

   每部分的面积大约为 2376 平方英尺。

5. 解决这个问题有很多不同的方法。以下是一种可能的解决方案。

   首先，计算红色环的面积，就好像它完全绕着圆圈一样

   $A=A_{\text{total}}-A_{\text{gold}}\,\!$

   $A=\pi \left({\frac {2}{3}}\cdot 33\right)^{2}-\pi \left({\frac {1}{3}}\cdot 33\right)^{2}$

   $A=\pi \cdot 22^{2}-\pi \cdot 11^{2}\,\!$

   $A=484\pi -121\pi =363\pi \,\!$

   $A\approx 1140.4{\text{ in}}^{2}\,\!$

   

   接下来，计算形成“c”开口的整个扇形的面积。

   $A={\frac {1}{2}}r^{2}\theta$

   $A={\frac {1}{2}}(22)^{2}\left({\frac {\pi }{4}}\right)$

   $A\approx 190.1{\text{ in}}^{2}\,\!$

   

   然后，计算黄色扇形的面积，并从之前的答案中减去它。

   $A={\frac {1}{2}}r^{2}\theta$

   $A={\frac {1}{2}}(11)^{2}\left({\frac {\pi }{4}}\right)$

   $A\approx 47.5{\text{ in}}^{2}\,\!$

   $190.1-47.5=142.6{\text{ in}}^{2}\,\!$

   最后，从第一个计算出的面积中减去这个答案。

   

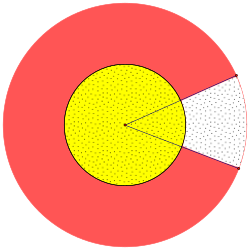
   面积约为 998 平方英寸。

本材料改编自原始的 CK-12 图书，可在此处找到 此处。本作品根据知识共享署名-相同方式共享 3.0 美国许可协议授权。