高中三角学/弧度制

在本课中，您将被介绍到弧度作为三角学中常用的角度单位。熟练地在度数和弧度之间进行转换非常重要。最终，就像学习一门外语一样，当您可以学会用弧度“思考”而不是总是从度数转换时，您将对弧度制感到舒适。最后，我们将回顾基于 30 度、45 度和 60 度旋转的基本三角函数的计算。

学习目标

• 定义弧度制。
• 将角度度数转换为弧度，并将弧度转换为角度。
• 计算以弧度或角度表示的特殊角的六个三角函数的值。

了解弧度制

许多度量单位来自看似随意和古老的根源。一些甚至随着时间的推移而改变。例如，米最初旨在基于地球的周长，现在有一个基于特定频率的相干光的周期数（波长）的极其复杂的科学定义！我们通常使用度数来测量角度，就像我们使用秒来表示分钟，使用分钟来表示小时一样。所有 60 和 12 的倍数，西方文明从大约 60 个世纪前发明的古苏美尔帝国的六十进制系统中继承下来，或多或少——当时时尚的场景是文明的摇篮，大多数部落是游牧民族，勉强维持生计，不会饿死。

度数到底是什么？一个度数是围绕圆形旋转的完整旋转的 1/360^th。弧度是三角学中用于测量角度的替代单位，有时被称为自然角。让我们看看为什么可能是这样。

顾名思义，弧度基于圆形的半径。事实证明，精确地一弧度是由在单位圆的弧上弯曲单位半径的长度（弧的长度）所产生的角度。一弧度的旋转、与该弧度长度相同的半径和所描绘的一弧度长度的弧——这实际上是“圆形一弧度段的弧长”。反过来：假设一个长度，用该长度做一个圆，称其为单位（一或底），并在圆周上测量相同的长度。无论长度是多少，该角度始终是一个弧度。
是否有另一个原因它可能被称为自然角，也许一个与三角学中的 TRI（意思是 THREE）相关的理由，这是我们的研究主题？顺便说一句，你可能听说过常数 PI（'π'），甚至可能知道它大约是 3.1459 个东西。什么东西？{{efn|关于 PI ('π') 的历史 你会猜是 3.1459 弧度，并且是正确的吗？让我们通过单位分析看看什么抵消了什么保留。从上面推断，我们是否不能写

段（长度） = 角（弧度）⋅ 半径长度) ⇔ s = (∅ ⋅ r)，其中 's' 是弧长的常用变量，因此为了使方程与长度作为单位相平衡，弧度必须为 [ 1/(长度/旋转角) ]——这归结为旋转角 因为弧度基于圆形的实际部分而不是任意划分，所以它是高等数学中更自然的角度单位，当您继续学习微积分时它将特别有用。

如果我们要绕圆形旋转一圈怎么办？继续添加半径长度，我们发现需要超过 6 个半径长度才能完成旋转。

但完整旋转的弧长实际上是周长！周长等于半径长度的 2π 倍。2π 大约为 6.28，因此周长略大于 6 个半径长度。或者，用弧度制表示，完整旋转（360 度）为 2π 弧度。

以此为起点，我们可以轻松找到其他角度的弧度制。因此，旋转的一半，即 180 度，必须为 π 弧度，而 90 度必须为二分之一 π。完成下面的表格

表 2.1

角度（度数）	角度（弧度）
90	${\tfrac {\pi }{2}}$
45
30
60
75

因为 45 是 90 的一半，所以二分之一 π 的一半是四分之一 π。30 是直角的三分之一，所以相乘得到

${\frac {\pi }{2}}\cdot {\frac {1}{3}}={\frac {\pi }{6}}$

并且因为 60 是 30 的两倍

$2\cdot {\frac {\pi }{6}}={\frac {2\pi }{6}}={\frac {\pi }{3}}$

这是完成的表格

表 2.2

角度（度数）	角度（弧度）
90	${\tfrac {\pi }{2}}$
45	${\tfrac {\pi }{4}}$
30	${\tfrac {\pi }{6}}$
60	${\tfrac {\pi }{3}}$
75	${\tfrac {5\pi }{12}}$

最后一个值是通过添加 30 和 45 的弧度制找到的

${\frac {\pi }{4}}+{\frac {\pi }{6}}=$	${\frac {3\cdot \pi }{3\cdot 4}}+{\frac {2\cdot \pi }{2\cdot 6}}$
${\frac {3\pi }{12}}+{\frac {2\pi }{12}}=$	${\frac {5\pi }{12}}$

可能你已经发现了一个将弧度与角度互换的公式，我们很快就会讨论它，但大多数你常用的角度都可以从这张表的值中轻松找到，所以根据圆周学习它们可以极大地提高你对弧度的理解。例如，大多数学生发现记住30和60很容易。30是π的六分之一，60是π的三分之一。如果你知道这些角度，你就可以找到任何以30和60为参考角的特殊角度，因为它们都具有相同的分母。同样，π的四分之几的倍数（45度）和π的二分之一的倍数（90度）也是如此。

弧度“计数”

你还记得小时候在芝麻街看伯爵吗？他会数苹果之类的物体，“一个苹果，两个苹果，三个苹果……”然后发出邪恶的笑声，周围响起闪电和雷声。嗯，要成功地使用弧度制，你需要重新学习用弧度而不是苹果来计数。让我们开始计数直角，实际上是${\tfrac {\pi }{2}}$弧度。

“一个π的二分之一，两个π的二分之一（实际上就是π），三个π的二分之一，四个π的二分之一（实际上就是2π）”

图2.1：用弧度制表示的90度旋转。

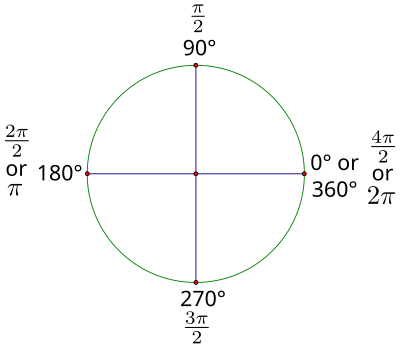图2.1：用弧度制表示的90度旋转。

你刚刚用一次旋转涵盖了所有90度的倍数的角度。

以下是45度角的图示

图2.2：45度旋转。

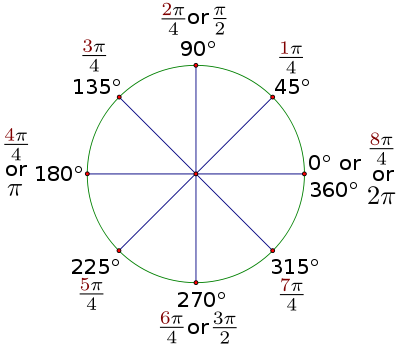图2.2：45度旋转。

请注意，图中额外的角度的参考角都是45度，它们的弧度值都是${\tfrac {\pi }{4}}$的倍数。通过计算${\tfrac {\pi }{3}}$和${\tfrac {\pi }{6}}$的倍数，完成以下弧度值。

图2.3：60度参考角。 图2.3：60度参考角。

图2.4：30度参考角。 图2.4：30度参考角。

图2.5：60度参考角的弧度制表示，经过一次旋转。

图2.5：60度参考角的弧度制表示，经过一次旋转。

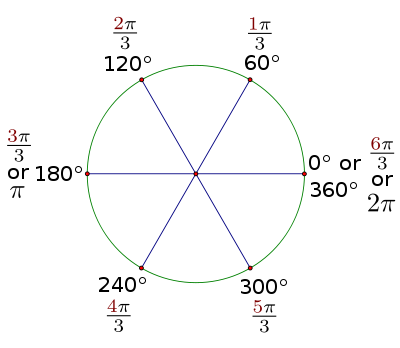图2.6：30度参考角的弧度制表示，经过一次旋转。

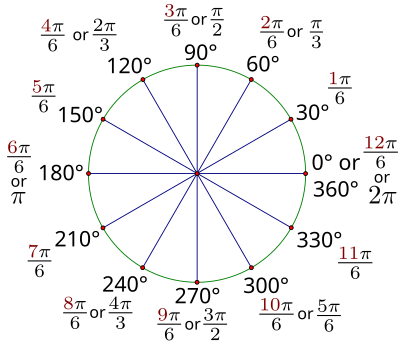图2.6：30度参考角的弧度制表示，经过一次旋转。

请注意，所有具有60度参考角的角度都是${\tfrac {\pi }{3}}$的倍数，而所有具有30度参考角的角度都是${\tfrac {\pi }{6}}$的倍数。如果你能学会用这些术语来计数，而不是总是将角度转换回度，它将帮助你有效地处理大多数你会遇到的弧度值。

对于其他示例，有一个公式。记住，

$\pi {\text{ radians}}=180{\text{ degrees}}\,\!$

如果你将这个等式的两边都除以180，你就会发现这个便于转换的公式

${\frac {\pi }{180}}{\text{ radians}}=1{\text{ degree}}$

所以

${\text{radians}}\cdot {\frac {180}{\pi }}={\text{degrees}}$

如果我们有一个度数，并希望将其转换为弧度，那么对上述等式进行运算得到

${\text{degrees}}\cdot {\frac {\pi }{180}}={\text{radians}}$

示例 1 将 ${\tfrac {11\pi }{3}}$ 转换为度数。 解: 如果按照上一节的内容，你应该认识到这个角度是 ${\tfrac {\pi }{3}}$（或 60 度）的倍数，因此在这个角度中有 11 个独立的 ${\tfrac {\pi }{3}}$：${\tfrac {\pi }{3}}$ · 11 = 60 · 11 = 660°。 以下是使用公式的结果 ${\text{radians}}\cdot {\frac {180}{\pi }}=$ ${\text{degrees}}\,\!$ ${\frac {11\pi }{3}}\cdot {\frac {180}{\pi }}=$ $11\cdot 60=660^{\circ }\,\!$

示例 2 将 −120° 转换为弧度制。答案用 π 表示。 解: 使用公式 ${\text{degrees}}\cdot {\frac {\pi }{180}}=$ ${\text{radians}}\,\!$ $-120\cdot {\frac {\pi }{180}}=$ ${\frac {-120\pi }{180}}$ 简化到最低项得到 $-{\frac {2\pi }{3}}$ 但是，你也可以意识到 120 是 2 · 60。因为 60° 是 ${\tfrac {\pi }{3}}$ 弧度，则 120 是 2 个独立的 ${\tfrac {\pi }{3}}$，或者 ${\tfrac {2\pi }{3}}$。将其变为负数，你就得到了答案，−${\tfrac {2\pi }{3}}$.

示例 3 将 ${\tfrac {11\pi }{12}}$ 弧度表示为度数。 解: ${\frac {11\pi }{12}}\cdot {\frac {180}{\pi }}=$   $11\cdot 15=\,\!$ $165^{\circ }$

弧度、度数和计算器

大多数科学计算器和图形计算器都有一个[MODE]设置，可以让你在弧度和度数之间进行转换，或者使用任一单位来寻找三角函数的近似值。重要的是，如果你使用计算器来估计三角函数，你应该知道你正在使用的模式。请看以下屏幕

sin(30)

-.9880316241

如果你希望找到 30 度 的正弦，你会根据上一章意识到有些问题，因为它应该是 ${\tfrac {1}{2}}$。事实上，正如你可能已经猜到，计算器将它解释为 30 弧度。在这种情况下，将模式改为度数并重新计算会给出预期结果。

sin(30)

-.9880316241

sin(30)

.5

科学计算器通常会有一个 3 个字母的显示，显示为DEG或RAD来告诉你你正在使用的模式。在计算三角比率之前一定要检查!

例 4 求 ${\tfrac {3\pi }{4}}$ 的正切。 解: 首先，如果你使用计算器来寻找答案，那你就太丢人了! 你应该知道这个! ${\tfrac {3\pi }{4}}$ 是一个第二象限角，其参考角为 ${\tfrac {\pi }{4}}$（45 度）。${\tfrac {\pi }{4}}$ 的正切是 1，因为正切在第二象限为负，所以答案是 -1。为了在你的计算器上验证这一点，确保模式设置为 弧度，并计算 ${\tfrac {3\pi }{4}}$ 的正切。 tan(3π/4) -1

例 5 求 cos $\left({\tfrac {11\pi }{6}}\right)$ 的值，保留四位小数。 解: 再次，您应该根据之前的工作知道确切的值。 ${\tfrac {11\pi }{6}}$ 的参考角是 ${\tfrac {\pi }{6}}$（30 度），并且 ${\tfrac {\pi }{6}}$ 的符号是 ${\tfrac {\sqrt {3}}{2}}$。因为 ${\tfrac {11\pi }{6}}$ 在第四象限，因此余弦为正，因此确切答案为 ${\tfrac {\sqrt {3}}{2}}$。使用计算器得到 cos(11π/6) .8660254038 四舍五入后，结果为 0.8660。您也可以使用计算器验证它确实是我们确切答案的非常好的近似值。 cos(11π/6) .8660254038 √(3)/2 .8660254038

示例 6 将 1 弧度转换为度数。 解: 许多学生习惯使用 π 来表示弧度，因此他们错误地认为 1 弧度表示 1π 弧度。虽然用 π 表示弧度更方便更常见，但不要忘记，π 弧度实际上是一个数字！它指定了大约 3.14 个半径长度旋转所形成的角度。因此，1 弧度是由长度仅为单个半径的弧所形成的旋转。回顾图 1.1。您估计这个角的度数是多少？它显然是锐角，并且看起来类似于 60° 角。为了找到更接近的近似值，我们将需要公式和计算器。 ${\text{radians}}\cdot {\frac {180}{\pi }}={\text{degrees}}$ 所以 1 弧度将是 ${\tfrac {180}{\pi }}$ 度。使用任何科学计算器或绘图计算器都可以得到这个度数的合理近似值，大约为 57.3°。 180/π 57.29577951

示例 7 找到具有 sin θ = 0.7071 的锐角θ 的弧度。 解: 首先，重要的是要理解，您的计算器很可能不会以 π 表示弧度，而是以小数近似值表示。在这种情况下，您需要使用反正弦函数。 sin-1(.7071) .7853885734 这个答案可能看起来并不熟悉，但 0.7071 可能听起来很熟悉。它是 ${\tfrac {\sqrt {2}}{2}}$ 的一个近似值。因此，如您所知，这实际上是一个 45° 角。的确，评估 ${\tfrac {\pi }{4}}$ 将表明计算器正在给出其对弧度测量的最佳近似值。 sin-1(.7071) .7853885734 π/4 .7853981634 如果它们并非完全相同让您感到困扰，很好，应该这样！请记住，0.7071 只是 ${\tfrac {\pi }{4}}$ 的一个近似值，因此我们已经从一定的舍入误差开始。

课程总结

角度可以用度数或弧度来衡量。弧度是由等于弯曲在圆周上的半径长度的弧长定义的角度。围绕圆周的一次完整旋转，或 360° 等于 2π 弧度。要从度数转换为弧度，请使用以下公式

${\text{degrees}}\cdot {\frac {\pi }{180}}={\text{radians}}$

要从弧度转换为度数，公式变为

${\text{radians}}\cdot {\frac {180}{\pi }}={\text{degrees}}$

就像学习外语需要记忆词汇才能取得成功一样，如果你熟悉象限角的弧度制（90° = ${\tfrac {\pi }{2}}$, 180° = π, 270° = ${\tfrac {3\pi }{2}}$, 360° = 2π) 和特殊角（30° = ${\tfrac {\pi }{6}}$, 45° = ${\tfrac {\pi }{4}}$, 60° = ${\tfrac {\pi }{3}}$），对你理解和使用弧度制将大有帮助。

复习问题

1. 右边的图片是出售奶酪的商店的招牌。

   (a) 估计圆中缺失部分的角度大小（度数）。

   (b) 将度数转换为弧度制。

   (c) 剩余奶酪部分的弧度是多少？

2. 将以下度数转换为弧度制，结果用 π 表示，不要使用小数近似值。

   (a) 240°

   (b) 270°

   (c) 315°

   (d) −210°

   (e) 120°

   (f) 15°

   (g) −450°

   (h) 72°

   (i) 720°

   (j) 330°

3. 将以下弧度制转换为度数

   (a) ${\tfrac {\pi }{2}}$

   (b) ${\tfrac {11\pi }{5}}$

   (c) ${\tfrac {2\pi }{3}}$

   (d) $5\pi \,\!$

   (e) ${\tfrac {7\pi }{2}}$

   (f) ${\tfrac {3\pi }{10}}$

   (g) ${\tfrac {5\pi }{12}}$

   (h) $-{\tfrac {13\pi }{6}}$

   (i) ${\tfrac {8}{\pi }}$

   (j) ${\tfrac {4\pi }{15}}$

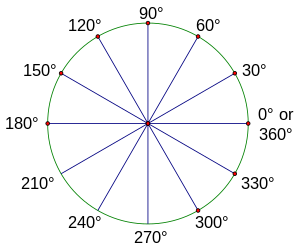
4. 图中显示了所有象限角以及参考角为 30°、45° 和 60° 的角。在内圆上，用 π 表示所有角的弧度制；在外圆上，用度数表示所有角。
   
5. 使用计算器，找出每个弧度角的度数近似值（精确到小数点后一位）。

   (a) ${\tfrac {6\pi }{7}}$

   (b) 1 弧度

   (c) 3 弧度

   (d) ${\tfrac {20\pi }{11}}$

6. 吉娜想计算 210 的正弦值，并在她的计算器上得到了以下答案

   sin(210)

   .4677185183

   (a) 写出正确的答案。

   (b) 解释她错在哪里。

7. 完成以下表格。将你的答案写成最简根式。

   x	sin(x)	cos(x)	tan(x)
   ${\frac {5\pi }{4}}$
   ${\frac {11\pi }{6}}$
   ${\frac {2\pi }{3}}$
   ${\frac {\pi }{2}}$
   ${\frac {7\pi }{2}}$

答案回顾

1.  

   (a) 答案可能会有所不同，但 120° 似乎比较合理。

   (b) 根据 (a) 部分的答案，合理的答案应该是 ${\tfrac {2\pi }{3}}$

   (c) 同样，根据 (a) 部分的答案，${\tfrac {4\pi }{3}}$

2.  

   (a) ${\tfrac {4\pi }{3}}$

   (b) ${\tfrac {3\pi }{2}}$

   (c) ${\tfrac {7\pi }{4}}$

   (d) $-{\tfrac {7\pi }{6}}$

   (e) ${\tfrac {2\pi }{3}}$

   (f) ${\tfrac {\pi }{12}}$

   (g) $-{\tfrac {5\pi }{2}}$

   (h) ${\tfrac {2\pi }{5}}$

   (i) $4\pi$

   (j) ${\tfrac {11\pi }{6}}$

3.  

   (a) 90°

   (b) 396°

   (c) 120°

   (d) 540°

   (e) 630°

   (f) 54°

   (g) 75°

   (h) −210°

   (i) 1440°

   (j) 48°

4. 
5.  

   (a) 154.3°

   (b) 57.3°

   (c) 171.9°

   (d) 327.3°

6.  

   (a) 正确答案是 $-{\tfrac {1}{2}}$

   (b) 她的计算器处于错误的模式，她计算的是 210 弧度 的正弦值。

7. x	sin(x)	cos(x)	tan(x)
   ${\frac {5\pi }{4}}$	$-{\frac {\sqrt {2}}{2}}$	$-{\frac {\sqrt {2}}{2}}$	$1\,\!$
   ${\frac {11\pi }{6}}$	$-{\frac {1}{2}}$	${\frac {\sqrt {3}}{2}}$	$-{\frac {\sqrt {3}}{3}}$
   ${\frac {2\pi }{3}}$	${\frac {\sqrt {3}}{2}}$	$-{\frac {1}{2}}$	$-{\sqrt {3}}$
   ${\frac {\pi }{2}}$	1	0	未定义
   ${\frac {7\pi }{2}}$	−1	0	未定义

此材料改编自原始的 CK-12 书籍，可在 此处 找到。本作品采用知识共享署名-相同方式共享 3.0 美国许可协议授权。