历史地质学/放射性衰变
作为对放射性年代测定文章的序言,读者应该了解放射性衰变机制。本文提供了对它是什么以及它是如何工作的非技术性解释。
读者应该从高中回忆起原子的原子核由质子(带正电荷的粒子)和中子(不带电荷的粒子,其质量几乎与质子相同)组成。原子核被电子云包围,电子是带负电荷的粒子,其重量可以忽略不计。电子的数量等于质子的数量。
原子中质子的数量是它的原子序数,质子和中子的总和给出它的原子量。
原子的化学性质由其电子的行为决定,因此实际上由其原子序数决定。因此在化学中,原子根据其原子序数被分类为元素:例如,像碳这样的元素被定义为具有 6 的原子序数。然而,两个原子可以具有相同的原子序数但不同的原子量。因此,例如,12C(碳-12)具有 6 个质子和 6 个中子,而14C(碳-14)具有 6 个质子和 8 个中子。它们都是碳,它们在化学上都表现得像是碳,但它们具有不同的原子量。因此,它们被称为是同一元素,即碳,但它们是碳的不同同位素。同位素由其原子序数和原子量定义。
在上一段的示例中,我们展示了用于同位素的符号。具有 6 个质子和 8 个中子的原子写为14C。它具有 6 个质子的事实是由“C”揭示的,这是碳的化学符号;根据定义,所有碳原子都具有 6 个质子。它具有 8 个中子的事实是由写在“C”左侧上方的“14”揭示的:这是同位素的原子量,因此由于原子量是质子和中子的数量,并且由于所有碳原子都具有 6 个质子,这告诉我们碳的这种同位素必须具有 8 个中子。
放射性衰变可以定义为任何自发事件,这些事件会改变原子核的状态,在此过程中从原子核中释放能量。除了伽马衰变(这里我们无需关心),这将涉及改变质子或中子的数量,或两者都改变,因此也会改变原子序数、原子量或两者都改变。
衰变可能发生的机制有很多。对于我们的目的,最重要的机制是

- α 衰变。在这种衰变形式中,原子核会发射一个由两个中子和两个质子组成的α 粒子,使原子序数减少两个,原子量减少四个。
- β 负衰变。在这种衰变形式中,原子中的一个中子通过原子发射一个电子而被转化为一个质子。因此,原子序数增加一个,而原子量保持不变。
- β 正衰变。在这种衰变形式中,一个质子通过发射一个正电子(一种类似于电子但带正电荷的粒子)而被转化为一个中子,结果是原子序数减少一个,而原子量保持不变。
- 电子俘获。在这种衰变形式中,原子自身的一个电子与它自己的一個质子结合,将质子转化为一个中子。这使原子序数减少一个,同时使原子量保持不变。
当衰变发生时,原始原子被称为母原子,而衰变产生的新原子被称为子原子。那些由放射性衰变产生的同位素被称为放射成因。并非所有同位素都会发生衰变:那些会发生衰变的被称为不稳定同位素(或放射性同位素),反之,那些不会发生衰变的被称为稳定同位素。因此,例如,12C 是稳定的,并将永远保持12C;相反,14C 不稳定,并倾向于衰变为14N(氮-14)。正如我们从这个例子中看到的,同一元素的不同同位素在稳定性上有所不同是完全可能的。
读者应该注意,当母原子衰变为子原子时,子原子不一定稳定;有时子原子将进一步发生衰变。这种情况被称为衰变链。
理解放射性衰变如何以及为什么发生很重要。根据物理学家的说法,放射性衰变是随机发生的:一个(例如)22Na(钠-22)原子会发生β 衰变并产生一个22Ne(氖-22)原子,仅仅是因为它的号码出来了。
原子的年龄与之无关。以类比为例,一个人用六发左轮玩俄罗斯轮盘赌。他每次玩都有 1/6 的几率死亡,无论他玩了多长时间都是如此。放射性衰变也是如此。如果我们有一个22Na 原子,那么无论它有多老,它在接下来的 2.6 年内都有 50% 的几率衰变;如果它在 2.6 年内幸存下来,那么它在接下来的 2.6 年内有 50% 的几率衰变;等等。
考虑一下如果我们有一个大的22Na 样本这意味着什么。因为样本很大,它的行为将非常接近我们对其统计期望值:因此,在 2.6 年后,50% 的原子将衰变为22Ne;在接下来的 2.6 年后,剩余的22Na 的 50% 将衰变(只剩下原始22Na 的 25%);在接下来的 2.6 年后,这些22Na 原子的 50% 将衰变,剩下原始样本的 12.5%;等等。
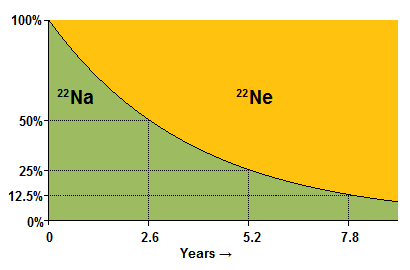
这个 2.6 年的数字被称为22Na 的半衰期:也就是说,一个22Na 原子有 50% 的几率衰变的时间;或者,等效地,我们统计期望值是样本的 50% 衰变的时间。
这种情況在数学上是众所周知的,可以用指数衰减方程表示
- N(t) = N0 × 2-t/2.6
其中,N0 是22Na 的原始数量,2.6 是以年为单位的半衰期,t 是以年为单位测量的经过时间,N(t) 是时间t 时样本中剩余的22Na 的数量。
这种情况可以用右边的图表来表示。
为了便于解释,我们始终使用22Na 作为示例,但相同的规则适用于所有放射性同位素,唯一的区别是不同同位素的半衰期不同:例如107Pd(钯-107)的半衰期为 650 万年。
人们有时会对这样的陈述感到惊讶:他们问道,当我们没有观察107Pd 样本 650 万年来验证它需要多长时间才能让它的一半衰变时,我们怎么能说呢?
然而,这并不是一个真正的问题。毕竟,以类比为例,警察无需观察你的汽车一个小时才能报告你正以 72 公里/小时的速度行驶。观察你在一秒钟内行驶 20 米就足够了,然后进行计算。
同样,如果我们只花一年观察一个107Pd 样本,并发现在这段时间内,该样本只有 0.0000106638% 衰变,那么我们可以写
- 100 - 0.0000106638 = 100 × 2-1/h
然后解方程求解h 将得到以年为单位的半衰期。
从这个例子中可以明显看出,我们对半衰期的了解的准确性将取决于我们对样本初始大小和其衰变速率的测量准确性。
因此,每个不稳定的同位素都有其自己的特征半衰期。更重要的是,对于每个同位素来说,这个半衰期是恒定的:它是同位素的一个属性,几乎不受外部环境的影响。
我们如何知道这一点?首先,从原理上讲应该是正确的:它可以从量子力学的基本定律推导出来。其次,它得到了实际观测的证实:在发现放射性衰变后不久,科学家就开始尝试通过将不稳定同位素置于热、压力、磁场等环境下改变其衰变速率,但结果是负面的。
在某些同位素中,根据它们与其他化学物质形成的分子键的不同,观察到了微小的变化。例如,7Be(铍-7)的衰变速率会根据其所处化学环境的不同而变化约 1%。从理论上讲,7Be 应该特别容易受到这种影响:它是一个非常小的原子,并且通过电子俘获衰变。即便如此,这种变化也很小。出于同样的原因,在对 7Be施加强压后,也实现了更小的变化。
我们还应该提到奇特的同位素 187Re(铼-187)。由于原子核衰变时释放的能量非常小,因此可以通过电离改变其半衰期。如果它完全剥夺了所有电子,它的半衰期将从 430 亿年下降到 33 年!然而,由于这种情况在地球上除物理实验室外不会发生,因此在所有地质目的中,我们可以将它的半衰期视为 430 亿年。
因此,为了真正影响同位素的半衰期,需要采用高度人工的方法——例如将它丢入核反应堆的核心。在自然界,尤其是在岩石中,有充分的理论和观测理由得出结论,不稳定同位素将具有恒定或几乎恒定的半衰期,因此将以规律和可预测的方式发生衰变,并且已经发生了衰变。
敏锐的读者可能已经猜到了事情的发展方向。在不稳定同位素的衰变中,我们有一组自然过程,每个过程都以完全可预测的速率进行。
简单地说,放射性年代测定的理念是这样的。如果我们有一块岩石,并且知道岩石刚形成时所含的某种放射性同位素的原始数量,并且知道它的半衰期,并且能够准确测量目前岩石中该同位素的数量,那么我们就可以计算出岩石的年龄。或者,如果我们知道放射性同位素的子同位素的原始数量和目前数量,那么我们同样可以计算出岩石的年龄。这种绝对年代测定技术被称为 **放射性年代测定**。
但是,我们如何才能知道岩石的原始成分呢?这个问题的答案取决于我们谈论的是哪种放射性同位素;因此,现在是停止笼统地谈论,而是详细了解放射性年代测定的具体方法的时候了。这些将是接下来的几篇文章的主题。
