舍入误差

学习目标

识别溢出和下溢误差的来源
在十进制表示和浮点表示之间转换
理解计算机上浮点表示的 IEEE 754 标准
计算表示的机器ε。

整数溢出（误差）

整数如何在计算机上表示？

大多数计算机使用二进制补码表示。假设我们有 4 位来存储和操作一个整数，我们可能会遇到以下情况

 0111 (7)
+0001 (1)
-----
 1000 (-8)

括号中的数字是 2 的补码二进制整数表示的十进制值。结果显然是错误的，因为添加正数永远不会导致负数。错误的原因是结果超出了 4 位可以使用 2 的补码表示法存储的值范围。

以下示例由于相同的原因给出了错误的答案。无法存储前面的 1。

 1000 (-8)
+1111 (-1)
-----
10111 (7)

浮点数下溢（误差）

在数学中，数字具有无限精度，但数字（数字的表示）具有有限精度。三分之一 (1/3) 无法用十进制精确表示，否则它将需要无限多个数字，这是不可能的。类似地，0.2 无法用二进制精确表示，这意味着它的二进制表示不精确（近似）。

当在计算机上计算/计算数字时，数字的表示被操纵，结果很可能是不精确的。这是计算的一个重要限制。本质上，计算机必须被认为是我们模型的一部分，当我们以计算方式解决问题时。我们必须将计算机考虑在内，因为它是一个二进制计算机，它近似于十进制数。

一个浮点下溢或下溢发生在计算结果太小而无法存储时。下溢可能是由于指数的（负）溢出引起的。

11.1875_{10}

的二进制表示是什么？

定点表示

任何实数都可以用二进制表示为定点数。要将数字从其十进制（基数 10）表示转换为其二进制表示，我们需要分别将整数部分和小数部分转换为二进制，因为需要不同的方法。请查看以下资源，了解如何做到这一点 [1]。

使用固定数量的数字和固定的小数点，可表示值的范围是固定的。给定五个数字如下 $nnn.nn_{10}$ ，我们可以表示从 $0.01_{10}$ 到 $999.99_{10}$ 的正值。使用以下科学计数法 $nnn\times 10^{nn}$ ，我们可以表示从 $0.01_{10}$ 到 $99900_{10}$ 的正值，这远远大于定点表示的范围。

浮点表示

使用固定数量的数字，我们可以使用浮点格式表示更大范围的值。IEEE 754 格式是计算机中数字浮点表示的国际标准。一个 32 位浮点数（单精度）使用三个部分表示，如图所示：符号位、（有偏）指数和分数。

IEEE 754 单精度浮点数表示的值可以使用以下公式计算

(-1)^{sign}\times 1.fraction\times 2^{exponent-127}

例如，要以 IEEE 单精度浮点数格式存储 $0.15625_{10}=0.00101_{2}=1.01_{2}\times 2^{-3}$ ，我们需要存储一个符号位 $0$ （0 表示正数，1 表示负数），一个小数部分 $.01$ ，以及一个偏移指数 $-3_{10}+127_{10}=124_{10}=1111100_{2}$ 。由于除 0 外的所有数字在二进制“科学”表示中都有一个前导 1，这个 1 在 IEEE 754 格式中没有存储，以节省一个位。我们稍后会说明如何表示值 0。

偏移指数只是巧妙地利用了可用位来表示更多值，并使数字比较更快。我们将以 8 位指数为例。在上图中，我们有 8 位，可以表示 $2^{8}=256_{10}$ 个不同的值。位模式本身没有内在含义，因此我们可以用它们来表示任何我们想要的东西。绿色部分显示了这些位模式在被视为无符号整数的二进制表示时所表示的值。问题是我们也想要表示负值。一种简单的解决方案是将最左边的位视为符号位：0 表示正数，1 表示负数，这会导致两个零 $+0$ 和 $-0$ 。蓝色部分显示了当我们使用 2 的补码方案来表示正数和负数时，使用相同的一组位模式会发生什么。回想一下，2 的补码方案通常用于简化硬件设计，以便我们可以使用加法来进行减法：a - b 等同于 a + ( -b 的 2 的补码)。要获得正整数的 2 的补码，就是将所有位反转并加 1。现在所有减法都可以用一次反转和两次加法来完成。2 的补码表示的问题是，一个看起来“更大”的模式并不一定表示更大的值。

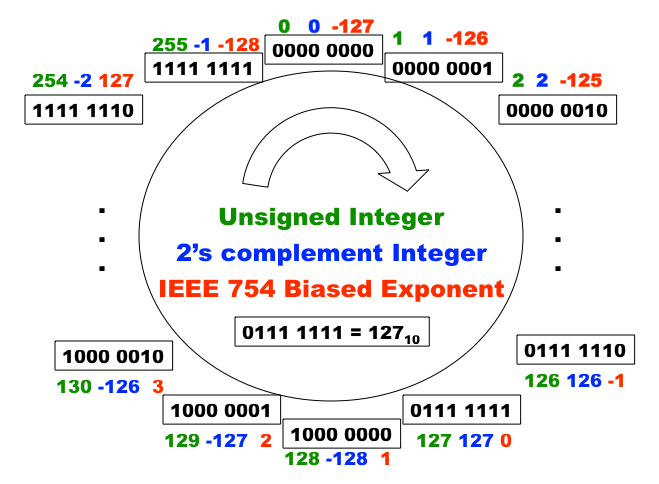
This figure shows how the biased exponent for IEEE 754 works. — 此图显示了 IEEE 754 的偏移指数是如何工作的。

红色部分显示了由相同一组位模式表示的偏移指数。正如你所看到的，一个看起来“更大”的模式总是表示更大的值，除了全为一的模式，它用于表示一个特殊的值。偏移指数表示的优点是每个值都由一个唯一的模式表示（没有两个零），并且比较浮点数更容易。指数放在 IEEE 754 标准中分数的前面，以便可以将浮点数按其位模式作为无符号整数进行比较（速度更快）。

下表显示了一些由特殊位模式表示的特殊值。

偏移指数	小数部分	数字
00...00	0	0
00...00	非零	非规格化
11...11	0	+/- 无穷大
11...11	非零	NaN（非数字）

因为总是将隐式/隐藏的 1 添加到小数部分以获得表示的值，所以需要一个特殊的模式来表示零值。现在，除以零的结果可以表示为 +/- 无穷大（整数运算中的除以零会导致程序崩溃）。 ${\sqrt {-4}}$ ，和 $0/0$ 可以表示为 NaN，这有助于调试你的程序。

这个数字的 IEEE 754 浮点数表示是什么：

-2.340625\times 10^{1}

这个 IEEE 754 浮点数的十进制等效值是什么：1100 0000 1111 0000 0000 0000 0000 0000？

最大的 IEEE 754 单精度浮点数是什么？

浮点型或科学计数法的缺点是什么？使用五个数字，我们可以用定点表示法精确地表示 $999.99_{10}$ 。但是，当我们使用以下科学/浮点表示法 $n.nn\times 10^{nn}$ 时，我们可以表示的最接近的值是 $9.99\times 10^{02}$ ，误差是 $999.99-999=0.99$ - 精度损失。

实数与浮点数数轴

这个图展示了实数和浮点数数轴的不同。可以做出以下观察结果

实数轴是连续的、稠密的、无限的。
浮点数（表示）轴是离散的、稀疏的、有限的。
一组实数用同一个浮点数（近似值）表示。
随着浮点数变大，组的大小也越来越大。

让我们研究一个具体的例子。使用四个小数位和定点表示法（ $nnn.n$ ），我们可以用相等距离表示 0、0.1、0.2、0.3、...、999.8、999.9。使用浮点表示法（ $+n.nn\times 10^{\pm n}$ ），我们可以表示的最小值为 $1.00\times 10^{-9}=0.\underbrace {0...0} _{8}1$ ，可以表示的最大值为 $1.11\times 10^{+9}=1110000000$ 。现在让我们看看这种浮点型数字格式在数轴上的某些点周围可以表示的值

在 0 旁边： $1.00\times 10^{-9}=0.\underbrace {0...0} _{8}1,1.01\times 10^{-9}=0.\underbrace {0...0} _{8}101,1.02\times 10^{-9}=0.\underbrace {0...0} _{8}102,...$ （连续数字之间的距离为 0.00000000001）
在 1 旁边： $1.00\times 10^{0}=1,1.01\times 10^{0}=1.01,1.02\times 10^{0}=1.02,...$ （连续数字之间的距离为 0.01）
在 10 旁边： $1.00\times 10^{1}=10,1.01\times 10^{1}=10.1,1.02\times 10^{1}=10.2,...$ （连续数字之间的距离为 0.1）
在 100 旁边： $1.00\times 10^{2}=100,1.01\times 10^{2}=101,1.02\times 10^{2}=102,...$ （连续数字之间的距离为 1）
在 1000 附近： $1.00\times 10^{3}=1000,1.01\times 10^{3}=1010,1.02\times 10^{3}=1020,...$ （相邻数字之间的距离为 10）