线性代数/集合、函数、关系

线性代数
← 证明技巧	集合、函数、关系	许可和历史 →

集合

数学家使用称为集合的集合。一个集合可以用大括号之间的列表表示，例如 $\{1,4,9,16\}$ ，或者，如果这很笨拙，可以使用集合生成器符号，例如 $\{x\,{\big |}\,x^{5}-3x^{3}+2=0\}$ （读作“所有 $x$ 的集合，使得……”）。我们用大写罗马字母为集合命名，例如素数 $P=\{2,3,5,7,11,\ldots \,\}$ ，除了少数特殊集合，例如实数 $\mathbb {R}$ 和复数 $\mathbb {C}$ 。为了表示某事物是集合的元素（或成员），我们使用“ ${}\in {}$ ”，因此 $7\in \{3,5,7\}$ ，而 $8\not \in \{3,5,7\}$ .

区分集合与任何其他类型集合的是外延原理，即两个具有相同元素的集合相等。由于这个原理，在集合中，重复项会合并 $\{7,7\}=\{7\}$ ，顺序也不重要 $\{2,\pi \}=\{\pi ,2\}$ .

我们使用“ $\subset$ "表示子集关系： $\{2,\pi \}\subset \{2,\pi ,7\}$ ，而“ $\subseteq$ "表示子集或相等（如果 $A$ 是 $B$ 的子集，但 $A\neq B$ ，那么 $A$ 是 $B$ 的**真子集**)。这些符号可以反转，例如 $\{2,\pi ,5\}\supset \{2,5\}$ .

由于外延性，要证明两个集合相等 $A=B$ ，只需要证明它们具有相同的成员。通常我们会证明互相包含，即 $A\subseteq B$ 和 $A\supseteq B$ 。

集合运算

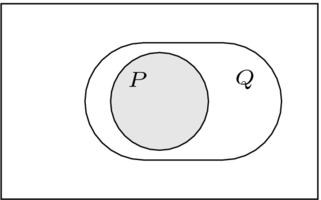
文氏图在这里很方便。例如， $x\in P$ 可以表示为

而“ $P\subseteq Q$ "看起来像这样。

注意，这与“如果……那么……”命题的图相同。这是因为“ $P\subseteq Q$ "意味着“如果 $x\in P$ ，那么 $x\in Q$ ”。

通常，对于每一个命题逻辑运算符，都有一个相关的集合运算符。例如， $P$ 的补集是 $P^{\text{comp}}=\{x\,{\big |}\,{\text{not }}(x\in P)\}$

并集是 $P\cup Q=\{x\,{\big |}\,(x\in P){\text{ or }}(x\in Q)\}$

而交集是 $P\cap Q=\{x\,{\big |}\,(x\in P){\text{ and }}(x\in Q)\}.$

}}当两个集合没有公共元素时，它们的交集就是空集 $\{\}$ ，用符号 $\varnothing$ 表示。根据蕴涵定义的“空真”性质，任何集合都包含空集作为子集。

序列

我们还将使用顺序重要的集合，且重复元素不合并。这些是序列，用尖括号表示： $\langle 2,3,7\rangle \neq \langle 2,7,3\rangle$ 。长度为 $2$ 的序列有时被称为有序对，用括号表示： $(\pi ,3)$ 。我们有时也说“有序三元组”、“有序 $4$ 元组”等等。集合 $A$ 中所有有序 $n$ 元组的集合记作 $A^{n}$ 。因此实数对的集合是 $\mathbb {R} ^{2}$ 。

函数

我们首先在初等代数中看到函数，它们被表示为公式（例如， $f(x)=16x^{2}-100$ ），但随着数学的深入，我们发现了更通用的函数——三角函数、指数函数和对数函数，甚至像绝对值这样的构造，它们涉及将部分拼凑在一起——我们看到函数不是公式，相反，关键在于函数将输入 $x$ 关联到一个唯一的输出 $f(x)$ 。

因此，函数或映射被定义为有序对的集合 $(x,f(x)\,)$ ，使得 $x$ 足以确定 $f(x)$ ，也就是说：如果 $x_{1}=x_{2}$ 那么 $f(x_{1})=f(x_{2})$ （这个要求被称为函数是良定义的）。\footnote{更多内容请参见同构部分}

每个输入 $x$ 是函数的自变量，每个输出 $f(x)$ 是一个值。所有自变量的集合是 $f$ 的定义域，输出值的集合是它的值域。通常我们不需要知道值域中有哪些和没有哪些，而是使用值域的超集，即陪域。函数 $f$ 的记号，定义域为 $X$ ，陪域为 $Y$ 是 $f:X\to Y$ 。

我们有时使用符号 $x{\stackrel {f}{\longmapsto }}16x^{2}-100$ ，读作“ $x$ 在 $f$ 下映射到 $16x^{2}-100$ ”，或者“ $16x^{2}-100$ 是 $x$ 的“像”。

一些映射，比如 $x\mapsto \sin(1/x)$ ，可以被认为是简单映射的组合，在这里， $g(y)=\sin(y)$ 应用于 $f(x)=1/x$ 的像上。 $g:Y\to Z$ 与 $f:X\to Y$ 的 **复合**，是将 $x\in X$ 映射到 $g(\,f(x)\,)\in Z$ 的映射。它记为 $g\circ f:X\to Z$ 。这个定义只有当 $f$ 的值域是 $g$ 的定义域的子集时才有意义。

观察到恒等映射 ${\mbox{id}}:Y\to Y$ 由 ${\mbox{id}}(y)=y$ 定义，具有以下性质：对于任何 $f:X\to Y$ ，复合函数 ${\mbox{id}}\circ f$ 等于 $f$ 。因此，恒等映射在函数复合中的作用类似于实数加法中的 0，或者类似于乘法中的 1。

根据这个类比，定义映射 $f:X\to Y$ 的左逆为一个函数 $g:{\text{range}}(f)\to X$ ，使得 $g\circ f$ 是 $X$ 上的恒等映射。当然， $f$ 的右逆为一个 $h:Y\to X$ ，使得 $f\circ h$ 是恒等映射。

一个既是 $f$ 左逆又是右逆的映射，简称为 **逆映射**。如果存在逆映射，那么它是唯一的，因为如果 $g_{1}$ 和 $g_{2}$ 都是 $f$ 的逆映射，那么 $g_{1}(x)=g_{1}\circ (f\circ g_{2})(x)=(g_{1}\circ f)\circ g_{2}(x)=g_{2}(x)$ （中间等式来自函数复合的结合律），因此我们通常称之为“逆映射”，记为 $f^{-1}$ 。例如，函数 $f:\mathbb {R} \to \mathbb {R}$ 的逆映射，该函数由 $f(x)=2x-3$ 给出，是函数 $f^{-1}:\mathbb {R} \to \mathbb {R}$ ，该函数由 $f^{-1}(x)=(x+3)/2$ 给出。

函数逆映射的 “ $f^{-1}$ " 符号可能令人困惑 - 它并不意味着 $1/f(x)$ 。之所以使用它，是因为它符合一个更大的体系。具有相同陪域和定义域的函数可以迭代，因此对于 $f:X\to X$ ，我们可以考虑 $f$ 与自身的复合： $f\circ f$ 和 $f\circ f\circ f$ 等等。

自然而然地，我们将 $f\circ f$ 写成 $f^{2}$ ，而 $f\circ f\circ f$ 写成 $f^{3}$ 等。注意，实数的熟悉指数规则显然成立： $f^{i}\circ f^{j}=f^{i+j}$ 和 $(f^{i})^{j}=f^{i\cdot j}$ 。与上一段的关系是，当 $f$ 可逆时，将 $f^{-1}$ 表示逆函数，将 $f^{-2}$ 表示 $f^{2}$ 的逆函数等，表明这些熟悉的指数规则在定义 $f^{0}$ 为恒等映射后仍然成立。

如果陪域 $Y$ 等于 $f$ 的值域，那么我们说该函数是满射（或映上）。一个函数有右逆当且仅当它是满射（这并不难验证）。如果没有任何两个参数共享一个像，如果 $x_{1}\neq x_{2}$ 意味着 $f(x_{1})\neq f(x_{2})$ ，那么该函数是单射（或内射）。一个函数有左逆当且仅当它是单射（这也不难验证）。

根据上一段，一个映射有逆函数当且仅当它既是满射又是单射；这样的函数被称为双射。它将定义域中的一个且仅一个元素与值域中的每个元素关联起来（例如，有限集必须具有相同数量的元素才能以这种方式匹配）。由于单射映射的复合是单射的，满射映射的复合是满射的，因此双射映射的复合是双射的。

我们有时希望缩小函数的定义域。例如，我们可以取函数 $f:\mathbb {R} \to \mathbb {R}$ ，它由 $f(x)=x^{2}$ 给出，为了使其具有逆函数，我们将输入参数限制为非负实数 ${\hat {f}}:\mathbb {R} ^{+}\to \mathbb {R}$ 。从技术上讲， ${\hat {f}}$ 是一个与 $f$ 不同的函数；我们称之为 $f$ 在较小定义域上的 **限制**。

关于函数的最后一点： $x$ 或 $f(x)$ 不必是数字。例如，我们可以将 $f(x,y)=x+y$ 视为一个函数，它以有序对 $(x,y)$ 作为参数。

关系

一些熟悉的运算显然是函数：加法将 $(5,3)$ 映射到 $8$ 。但是，“ $<$ ” 或 “ $=$ ” 呢？我们这里采用将 “ $3<5$ ” 改写为 “ $(3,5)$ 属于关系 $<$ ” 的方法。也就是说，定义集合 $A$ 上的二元关系 为 $A$ 元素的有序对的集合。例如， $<$ 关系是集合 $\{(a,b)\,{\big |}\,a<b\}$ ；该集合中的一些元素是 $(3,5)$ 、 $(3,7)$ 和 $(1,100)$ 。

自然数上的另一个二元关系是等式；该关系正式写成集合 $\{\ldots ,(-1,-1),(0,0),(1,1),\ldots \}$ 。

另一个例子是“比 $10$ 更接近”，集合 $\{(x,y)\,{\big |}\,|x-y|<10\}$ 。该关系中的一些成员是 $(1,10)$ ， $(10,1)$ 和 $(42,44)$ 。既不是 $(11,1)$ 也不是 $(1,11)$ 是成员。

这些例子说明了定义的普遍性。各种关系（例如，“两个数字都是偶数”或“第一个数字是第二个数字的数字颠倒”）都包含在定义中。

等价关系

我们需要正式地说明两个物体在某种程度上是相似的。虽然这些相似的物体并不相同，但它们是相关的（例如，两个整数“在被 $2$ 除后得到相同的余数”）。

二元关系 $\{(a,b),\ldots \}$ 当它满足以下条件时被称为**等价关系**

自反性：任何物体都与自身相关；
对称性：如果 $a$ 与 $b$ 相关，那么 $b$ 与 $a$ 相关；
传递性：如果 $a$ 与 $b$ 相关，并且 $b$ 与 $c$ 相关，那么 $a$ 与 $c$ 相关。

（为了看到这些条件正式化了“相同”，请再次阅读它们，将“与……相关”替换为“与……相似”。）

一些例子（在整数上）：“ $=$ " 是一个等价关系，" $<$ " 不满足对称性，“同号”是一个等价关系，而“比 $10$ 更近”不满足传递性。

划分

在“同号” $\{(1,3),(-5,-7),(-1,-1),\ldots \}$ 中，有两类数对，第一类是两个数都是正数，第二类是两个数都是负数。所以整数恰好落在两个类别之一：正数或负数。

集合 $S$ 的划分是指子集 $\{S_{1},S_{2},\ldots \}$ 的一个集合，使得 $S$ 中的每个元素都属于且仅属于一个 $S_{i}$ ： $S_{1}\cup S_{2}\cup \ldots {}=S$ ，并且如果 $i$ 不等于 $j$ ，那么 $S_{i}\cap S_{j}=\varnothing$ 。想象 $S$ 被分解成不同的部分。

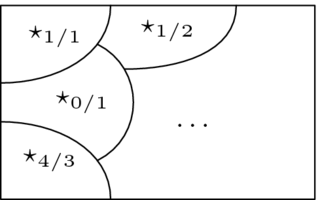
因此，第一段说“同号”将整数划分为正数和负数。

类似地，等价关系“=”将整数划分为单元素集。

另一个例子是分数。当然， $2/3$ 和 $4/6$ 是等价分数。也就是说，对于集合 $S=\{n/d\,{\big |}\,n,d\in \mathbb {Z} {\text{ and }}d\neq 0\}$ ，我们定义两个元素 $n_{1}/d_{1}$ 和 $n_{2}/d_{2}$ 等价，如果 $n_{1}d_{2}=n_{2}d_{1}$ 。我们可以检查这是否是一个等价关系，也就是说，它是否满足上述三个条件。有了它， $S$ 被分成若干部分。

在我们证明等价关系总是导致划分之前，我们首先说明这个论点。考虑两个整数之间“奇偶性相同”的关系，集合 $\{(-1,3),(2,4),(0,0),\ldots \}$ （即，“被 $2$ 除后得到相同的余数”）。我们想说自然数被分成两个部分，偶数和奇数，在一个部分内部，每个成员的奇偶性与其他成员相同。因此，对于每个 $x$ ，我们定义与它相关的数字集合： $S_{x}=\{y\,{\big |}\,(x,y)\in {\text{same parity}}\}$ 。一些例子是 $S_{1}=\{\ldots ,-3,-1,1,3,\ldots \}$ ，和 $S_{4}=\{\ldots ,-2,0,2,4,\ldots \}$ ，和 $S_{-1}=\{\ldots ,-3,-1,1,3,\ldots \}$ 。这些是部分，例如， $S_{1}$ 是奇数。

}}定理等价关系在基础集合上产生一个划分。

证明

将集合称为 $S$ ，关系称为 $R$ 。根据上段的说明，对于每个 $x\in S$ ，定义 $S_{x}=\{y\,{\big |}\,(x,y)\in R\}$ .

观察到，由于 $x$ 是 $S_{x}$ 的一个成员，所有这些集合的并集是 $S$ 。因此，如果我们能证明不同的部分是不相交的，那么我们就完成了：如果 $S_{x}\neq S_{y}$ ，那么 $S_{x}\cap S_{y}=\varnothing$ 。我们将通过逆否命题来验证这一点，也就是说，我们将假设 $S_{x}\cap S_{y}\neq \varnothing$ ，以便推导出 $S_{x}=S_{y}$ .

设 $p$ 是交集中的一个元素。根据 $S_{x}$ 和 $S_{y}$ 的定义，这两个 $(x,p)$ 和 $(y,p)$ 是 $R$ 的成员，并且由于这种关系的对称性， $(p,x)$ 和 $(p,y)$ 也是 $R$ 的成员。为了证明 $S_{x}=S_{y}$ ，我们将证明每个集合都是另一个集合的子集。

假设 $q\in S_{x}$ ，使得 $(q,x)\in R$ 。使用传递性以及 $(x,p)\in R$ 可以得出结论： $(q,p)$ 也是 $R$ 的元素。但是 $(p,y)\in R$ ，因此传递性的另一个应用表明 $(q,y)\in R$ 。因此 $q\in S_{y}$ 。所以 $q\in S_{x}$ 意味着 $q\in S_{y}$ ，因此 $S_{x}\subseteq S_{y}$ .