MATLAB 编程/向量和矩阵/矩阵运算

基本矩阵运算

加法和减法

如果两个矩阵的行数和列数相同，我们可以对它们进行加法和减法运算。

以下是一些示例

  >> a = [7,9,4;6,2,5]
  a =
     7     9     4
     6     2     5

  >> b=[2,0,1;4,7,3]
  b =
     2     0     1
     4     7     3

  >> % Addition of a and b matrices
  a+b
  ans =
     9     9     5
    10     9     8

  >> % Subtraction of a and b matrices
  a-b
  ans =
     5     9     3
     2    -5     2

矩阵乘法

对于矩阵乘法，有两种方法可以进行运算。

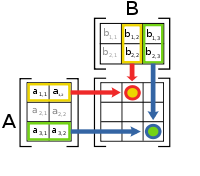
(i) 矩阵乘法（使用符号*或mtimes）

要求是第一个矩阵的列数必须等于第二个矩阵的行数。

如右侧示例所示，矩阵 A 有 3 X 2，矩阵 B 有 2 X 3

因此，2 X 3 <-> 3 X 2，因此满足上述要求。

此外，请注意，结果矩阵的大小取决于第一个矩阵的行数与第二个矩阵的列数。

>> A=[4,2,4;8,3,1]

A =
     4     2     4
     8     3     1

>> B=[3,5;2,8;7,9]

B =
     3     5
     2     8
     7     9

>> mtimes(A,B)

ans =
    44    72
    37    73

>> A*B

ans =

    44    72
    37    73

以下示例显示了如果矩阵维度不匹配会发生什么。

如所示，矩阵 C 有 5 X 4，矩阵 D 有 3 X 2

5 X 4 <-> 3 X 2，因此无法满足条件，也无法求解。

>> %Demonstrations what if matrices dimensions are incorrect 
>> C=randi(10,5,4)

C =

     2    10    10     3
     2    10     4     5
     3     5     2     1
     5     5     8     2
     1     4     4    10

>> D=randi(10,3,2)

D =

    10     3
     6     4
     1     9

>> mtimes(C,D)
Error using  * 
Incorrect dimensions for matrix multiplication. Check that the number of columns in the first
matrix matches the number of rows in the second matrix. To perform elementwise
multiplication, use '.*'.

(ii) 点积（注意：只有当两个矩阵大小相同时才能使用）以上面的示例为例，它不能求解方程，因为上面的矩阵 A 和 B 大小不同

>> A.*B % want to show dot product unable to solve this multiplication issues
Matrix dimensions must agree.

创建随机整数矩阵

要生成随机整数矩阵，可以键入以下内容 randi(IMAX,M,N)
注意：IMAX 是最大整数（从 1 开始），M * N 是矩阵

以下是一些示例

>> randi(50,3,4)

ans =
     9    14    42    48
    36     3    35     2
     2     5    16    22

转置

使用上面的矩阵，我们可以对矩阵进行转置。转置矩阵通常只是将行转换为列，将列转换为行。图示只是演示了转置操作。转置矩阵的应用之一是密码学。

有两种方法可以实现它。一种是在要转置的矩阵末尾添加 '，或者使用函数 transpose。

回到上面的幻方示例，我们将对其进行转置。我们可以看到，它沿着对角线转置看起来像这样 : \

  >> % transpose matrix c to d
  >> d = c'
  d =
    17    23     4    10    11
    24     5     6    12    18
     1     7    13    19    25
     8    14    20    21     2
    15    16    22     3     9

行列式

矩阵的行列式是一个特殊的数字，它只针对方阵定义。
行列式用于求解线性方程组并确定矩阵的逆矩阵。

2X2 矩阵的行列式 : $\mathbf {A} ={\begin{bmatrix}a&b\\c&d\\\end{bmatrix}}*|A|=ad-bc$

3X3 矩阵的行列式 : $\mathbf {A} ={\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}}*|A|=a(ei-fh)-b(di-fg)+c(dh-eg)$

>> A=[6,1,1;4,-2,5;2,8,7]

A =
     6     1     1
     4    -2     5
     2     8     7

>> det(A)
ans =
 -306.0000

逆矩阵

矩阵的逆矩阵是倒数矩阵，其公式表示为 ${A}^{-1}={\frac {1}{|A|}}adjA$
，其中 adj 代表矩阵的伴随矩阵。

注意：并非所有矩阵都有逆矩阵，如果它们的行列式等于零。

>>%matrix inversion using manual method

>> M=[2,-1,3;-5,3,1;-3,2,3]

M =

     2    -1     3
    -5     3     1
    -3     2     3

>> %First we find the matrix determinant
>> DM = det(M)

DM =
   -1.0000

>>%Since determinant IS NOT equal to 0, we can find the matrix inverses

>> AM = adjoint(M)
AM =
    7.0000    9.0000  -10.0000
   12.0000   15.0000  -17.0000
   -1.0000   -1.0000    1.0000

>> (1/DM)*AM

ans =
   -7.0000   -9.0000   10.0000
  -12.0000  -15.0000   17.0000
    1.0000    1.0000   -1.0000

%shortcut using function inv which should be same as manual calculation above
>> inv(M)

ans =
   -7.0000   -9.0000   10.0000
  -12.0000  -15.0000   17.0000
    1.0000    1.0000   -1.0000

现实生活中的应用

矩阵有许多应用，例如

密码学

矩阵用于加密消息代码。程序员使用矩阵来对字母进行编码或加密。消息由一系列二进制数字组成，这些数字使用编码理论来解决通信问题。因此，矩阵的概念用于求解此类方程。

要执行此矩阵运算，消息首先被分解成固定大小的块，每个块都表示为一个数字向量。公钥包含一个矩阵，称为加密矩阵或公钥矩阵，用于转换每个数字向量。然后将得到的转换后的向量乘以模数模幂，以获得密文。

% Define the message to encrypt
message = 'I LOVE MATLAB';

% Convert the message to a vector of numbers
message_vec = double(message);

% Define the public key parameters (modulus and exponent)
% Next, we define the public key parameters, which in this case are a modulus of 104729 and an exponent of 65537.
modulus = 104729;
exponent = 65537;

% Define the encryption matrix
% We also define an encryption matrix of size 2x2.
encryption_matrix = [3 5; 7 11];

% Break the message vector into blocks of length 2
block_size = 2;
num_blocks = ceil(length(message_vec) / block_size);
message_blocks = zeros(num_blocks, block_size);
message_blocks(1:length(message_vec)) = reshape(message_vec, [], block_size);

% Apply the encryption matrix to each message block
encrypted_blocks = mod(message_blocks * encryption_matrix, modulus);

% Raise each encrypted block to the exponent
exponentiated_blocks = mod(encrypted_blocks .^ exponent, modulus);

% Convert the encrypted blocks to a single vector of numbers
encrypted_vec = reshape(exponentiated_blocks, [], 1);

% Print out the encrypted message
fprintf('Encrypted message: %s\n', char(encrypted_vec'));

要解密消息，可以使用私钥，私钥包含两个部分：模数和模某个值的指数的逆。指数的逆用于将密文乘以一个幂，该幂将反转矩阵变换并恢复原始消息块。

% Define the encrypted message
encrypted_message = [16124 4546 84313 99848 16124 4546 84313 40458 16124 4546 84313 40458 32274 40458];

% Define the private key parameters (modulus and inverse exponent)
modulus = 104729;
inverse_exponent = 47027;

% Define the decryption matrix
decryption_matrix = [17 23; 21 29];

% Break the encrypted message vector into blocks of length 2
block_size = 2;
num_blocks = length(encrypted_message) / block_size;
encrypted_blocks = reshape(encrypted_message, block_size, num_blocks)';

% Raise each encrypted block to the inverse of the exponent
decrypted_blocks = mod(encrypted_blocks .^ inverse_exponent, modulus);

% Apply the decryption matrix to each decrypted block
decrypted_blocks = mod(decrypted_blocks * decryption_matrix, modulus);

% Convert the decrypted blocks to a single vector of numbers
decrypted_vec = reshape(decrypted_blocks, [], 1);

% Convert the decrypted vector to a string and print it out
fprintf('Decrypted message: %s\n', char(decrypted_vec'));

图像处理

矩阵运算在现实生活中的一种应用是图像处理。我们将研究一个比较简单的例子，例如图像模糊。

例如，我们希望对一张假设为黑白的图像进行模糊处理，这里展示了一个矩阵的示例，其中每个像素的值代表一个灰度值，从 1 到 255。

我们将使用矩阵卷积来计算图像中每个像素周围 3x3 邻域的像素值的平均值。

要应用此滤波器，我们将矩阵在图像的每个像素上滑动，并执行矩阵乘法。例如，要模糊图像中心的像素，您将获取其周围的 3x3 邻域，将每个像素值乘以模糊滤波器矩阵中的对应值，然后将结果相加。最终的值是模糊图像的新像素值。

我们对图像中的每个像素重复此过程，最终得到一张看起来更模糊的新图像。

% Define the input matrix
input_matrix = [1 2 3; 8 9 4; 7 6 5];

% Define the blur filter matrix
blur_filter = 1/9 * [1 1 1; 1 1 1; 1 1 1];

% Apply the filter using convolution
blurred_matrix = conv2(input_matrix, blur_filter, 'same');

% Display the original and blurred matrices side by side
disp('Original Matrix:');
disp(input_matrix);
disp('Blurred Matrix:');
disp(blurred_matrix);

电路分析

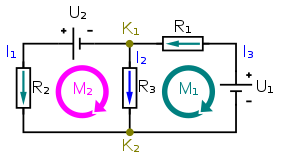
在电气工程中，基尔霍夫电压定律 (KVL) 指出，电路中闭合回路上的所有电压之和必须等于零。该定律可用于为具有 m 个回路的电路编写一组线性方程。这些方程可以排列在一个矩阵中，称为回路分支关联矩阵。

根据这些示例

回路 M1 : V1 - R1*I1 - R3*I2 = 0

回路 M2 : V2 - R2*I2 - R3*I1 = 0

[ R1 -R3 0 ] [ I1 ] = [ V1 ]

[-R3 R2+R3 -R2 ] [ I2 ] = [ -V2 ]

[ 0 -R2 1 ] [ V2 ] = [ 0 ]

使用符号数学工具箱，我们可以求解这些方程

% Define the symbolic variables
syms R1 R2 R3 V1 V2 I1 I2

% Define the Kirchhoff Voltage Law equations for each loop
eq1 = V1 - R1*I1 - R3*(I1-I2) == 0;
eq2 = V2 - R2*I2 - R3*(I2-I1) == 0;

% Define the Kirchhoff Current Law equation at node K1 and K2
eq3 = I1 - I2 == 0;

% Solve the system of equations for the currents and voltages
sol = solve(eq1, eq2, eq3, I1, I2, V2);

% Display the results
I1 = double(sol.I1);
I2 = double(sol.I2);
V2 = double(sol.V2);
fprintf('I1 = %.2f A\n', I1);
fprintf('I2 = %.2f A\n', I2);
fprintf('V2 = %.2f V\n', V2);

参考文献

^[1] ^[2] ^[3] ^[4]

[1] ttps://web.archive.org/web/20220712153202/https://collegedunia.com/exams/applications-of-determinants-and-matrices-and-solved-examples-mathematics-articleid-2195

[2] ttps://web.archive.org/web/20220719154910/https://www.embibe.com/exams/inverse-matrix/

[3] ttps://web.archive.org/web/20220814062118/https://www.theclickreader.com/dot-products-and-matrix-multiplication/

[4] ttps://web.archive.org/web/20220814062138/https://www.theclickreader.com/matrix-transpose-determinants-and-inverse/

[1]

[2]

[3]

[4]