电子材料/波粒二象性/双缝实验/理想

实验装置

双缝实验在理论上非常容易设置，它展示了波的一些非常有趣的特性，即使在量子物理之外也是如此。一个相干的单色波源被指向一块不透明屏上的两个缝隙。由于缝隙会衍射波，这将产生两个密切相关的光源

• 它们都具有相同的波长（因为原始光源是单色的）
• 它们都是相干的（波处于相位）

这在下面的图中以概念形式显示。这是一个非常简单的图表，但它有助于描述这个概念。

现在让我们为设置指定一些参数。我们将使用光源（如激光）产生波，其波长为 800nm。这正好位于可见光谱的红色端之外，人眼几乎看不到。然而，这是一个方便使用的数字，因为它很容易被除。如果你在现实生活中做这个实验，光很可能是大约 700nm（深红色）。我们将让我们的光穿过两个缝隙（我们假设这些缝隙非常窄，以至于衍射是完美的），间距为 0.1mm，正如我们将看到的，这会产生显著的效果，并且在实践中并不难实现。然后我们将我们的屏幕放置在距离缝隙 5 米的地方。所以，我们的参数是

• $\lambda =400\times 10^{-9}{\mbox{ m}}\,$
• $d=0.1\times 10^{-3}{\mbox{ m}}\,$
• $L=5{\mbox{ m}}\,$

假设我们的介质的折射率非常接近 1（如空气），我们也知道波速 c，因为这是一个普遍的常数

• $c=3\times 10^{8}{\mbox{ m s}}^{-1}$

因此我们可以计算出频率 f 和角频率 ω

• $f={\frac {c}{\lambda }}=375\times 10^{12}{\mbox{ Hz}}$
• $\omega =2\pi f=750\pi \times 10^{12}{\mbox{ rad s}}^{-1}$

也可以找到波数（每米的周期数） k

• $k={\frac {2\pi }{\lambda }}=2.5\pi \times 10^{6}{\mbox{ m}}^{-1}$.

单缝方程

让我们首先考虑从一个缝隙发出的波。如果我们假设缝隙非常长（是波长的很多倍）并且非常窄（远小于波长），并且激光发出的光是平面波（因此缝隙上每个点的相位都相同），那么我们可以说衍射波是圆柱形的

这可以通过波动方程直接证明。这意味着我们只需要考虑波前的“切片”，而不必担心垂直距离的影响（即缝隙方向），因为它不会影响波。在现实生活中，激光会产生一个紧密的亮点，因此产生的波是一个非常薄的圆柱形波（因为它没有被长缝隙垂直衍射）。

现在让我们考虑行波的方程。波在距离源 x 处和时间 t 处产生的扰动 u 由以下方程给出

$u\left(x,t\right)=A\left(x,t\right)\sin \left(kx-\omega t+\phi \right)$

其中 φ 是相位偏移量，从这里开始我们可以将其设置为零，因为我们处理的所有波都是同相的。A(x,t) 是波的振幅包络。为简单起见，我们假设波在这个实验中不会明显衰减。这是一个可以接受的简化，因为我们只关心波的相位关系。在现实生活中，圆柱形波的振幅与距离成反比（而不是球形波的距离平方）。

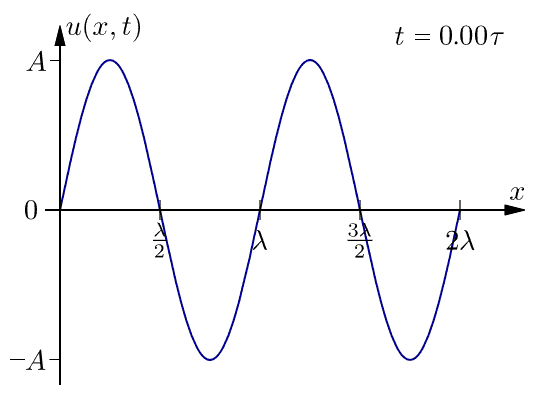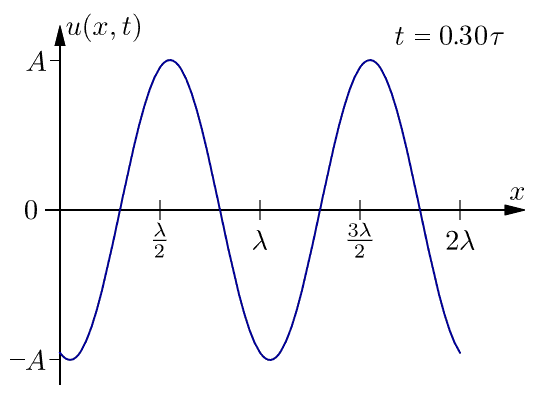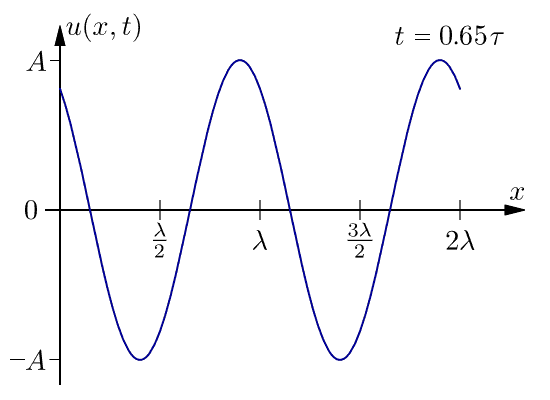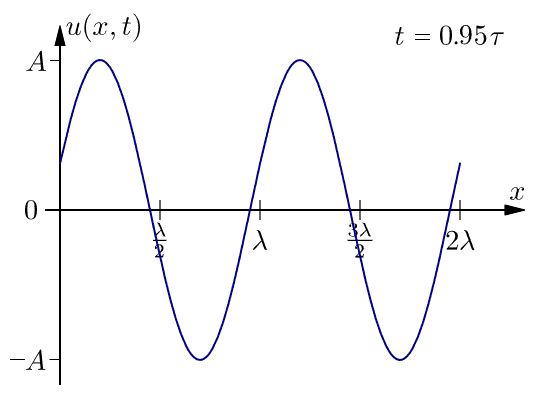
下面是在一个周期内一维行波的图。此波不会随着距离而衰减。

一维行波。您可以看到波在正 x 方向传播

现在，由于我们知道我们正在处理圆柱形波，我们只需要考虑整个系统的二维切片。我们将 x 和 y 轴设置为与页面顶部的图像中所示相同。在这种情况下，到 (x,y) 处的点的距离 r 由勾股定理给出

$r={\sqrt {x^{2}+y^{2}}}$

因此，我们二维空间中行波的方程式现在是（记住我们忽略了振幅和相位偏移）：

$u\left(x,y,t\right)=\sin \left(k{\sqrt {x^{2}+y^{2}}}-\omega t\right)$

下图显示了这个波在 t=0 时的样子。注意这个波在原点是不光滑的（你可以看到一个翻转过来的 - 实际上是相位差 180° - 的函数版本，这里）。如果这个波被动画化，它看起来像是向外流动。

我们可以使用以下公式，将其中一个点源定位在任意点 (x₀,y₀) 上：

$u\left(x,y,t\right)=\sin \left(k{\sqrt {(x-x_{0})^{2}+(y-y_{0})^{2}}}-\omega t\right)$

实验模型

现在我们可以构建我们的双缝实验模型。如果我们将光源放置在 $\left(\pm {\frac {d}{2}},0\right)$，我们就得到了我们想要的缝隙间距 d。因此，空间和时间中任意点的扰动公式由以下公式给出：

$u(x,y,t)=\sin \left(k{\sqrt {\left(x-{\frac {d}{2}}\right)^{2}+y^{2}}}-\omega t\right)+\sin \left(k{\sqrt {\left(x+{\frac {d}{2}}\right)^{2}+y^{2}}}-\omega t\right)$

我们的缝隙间距为 0.1mm，波长为 800nm。这意味着缝隙相隔 125 个波长，因此我们可以在一个合理大小的图表上很容易地识别出衍射图案。下面是我们的装置中衍射图案的密度图。黑色对应于最小振幅，白色对应于最大振幅，而中灰色对应于零振幅。我们现在只关注 y 值为正的情况，因为带有缝隙的屏幕在 y=0 处形成屏障。

我们可以清楚地看到交叉的图案，但我们无法直接看到任何“条纹”效应。这是因为条纹是波的平均值随位置变化的结果。事实上，图像中确实包含了条纹的微弱证据。你可能会注意到，波中有大约是径向的“带”，它们从白色变为黑色，然后再变回白色，还有一些带则保持在中灰色左右。这些带会随着时间保持在固定位置。跨越图像的带是波的周期性和行进性质的产物，这些带会随着时间推移而移动。当波在一段时间内平均后，条纹就会变得清晰可见。下图显示了同一区域的图，但与 b 中时间冻结的波不同，这个图是由波在时间上的多个样本组合而成的。亮区对应于合成的波振幅较高的位置，而黑区对应于波振幅为零的位置。

你可以在这里看到条纹，但它们非常靠近，肉眼无法轻易识别。此外，条纹也不是完美的径向（从单点发出），因此我们无法轻易确定它们的间距，除非绘制这个图。如果我们从更远的地方观察这个系统（如之前一样平均），我们就可以看到一个更简单的图案：

合成的波现在看起来像是一系列从缝隙发出（在这个尺度下缝隙不可见地分开）的径向线，这些线交替出现高低强度。正如我们在下一节中发现的那样，这使得一个非常有用的近似值是准确的。此外，条纹的间距也大得多，因此我们可以更容易地测量条纹间距。注意图的左下角的明显曲线 - 这里没有曲线，但规则的像素网格与倾斜的线结合在一起，会导致出现虚假图案。有关相关现象的更多信息，请参阅 莫尔纹 和 外差和拍频。

我们可以绘制一个 y=5m 处的波的图。下图是中央极大值，跨越一个波周期：

你无法在现实生活中看到这种振荡，因为可见光的频率极高（数百太赫兹）。然而，我们可以感知屏幕上的辐照度。（有关推导，请参阅此页面。现在，屏幕上某一点的辐照度 I 由以下公式给出：

$I=\epsilon v\langle \mathbf {E} ^{2}\rangle$

其中$\langle \mathbf {E} ^{2}\rangle$表示电场强度平方的时间平均值。这是场论的基本结果，这里不作证明。目前，由于我们正在处理相对强度，我们将省略常数并设置

$I=\langle \mathbf {E} ^{2}\rangle$

根据叠加原理，

$\mathbf {E} =\mathbf {E} _{1}+\mathbf {E} _{2}$

其中E₁和E₂是由每个狭缝产生的场的分量。现在我们可以写

$\mathbf {E} ^{2}=\left(\mathbf {E} _{1}+\mathbf {E} _{2}\right)^{2}$

$\mathbf {E} ^{2}=\mathbf {E} _{1}^{2}+\mathbf {E} _{2}^{2}+2\mathbf {E} _{1}+\mathbf {E} _{2}$

对该方程两边进行时间平均，得到

下图是 t=0 时中心的 5 个极大值。您可以轻松地看到波幅值高的规则极大值，以及波幅值非常小的极小值。您还应该能够看到强度变化类似于余弦波的绝对值。

您可以将此与现实生活中看到的条纹进行比较（上面的图案来自两个狭缝，下面的图案来自五个狭缝）

现在让我们找到系统物理属性和条纹间距之间的关系。

条纹间距的近似值

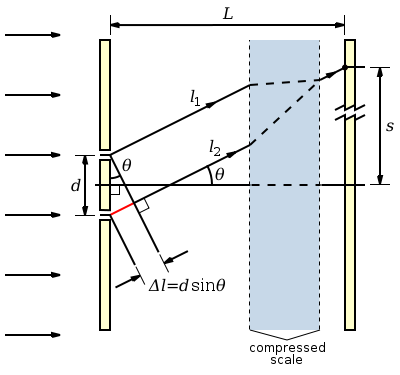
如果我们进行一些近似，就可以很容易地找到该系统中条纹间距的表达式。考虑右侧的图。它显示了两条光线，一条来自每个狭缝，都到达屏幕上的同一个点，用黑点标记。因为到屏幕的距离远大于狭缝之间的距离，所以这些光线实际上是平行的。

现在，下方的光线比上面的光线走得更远，我们将路径长度差称为Δl。这在图中用红色标记。对于完全的相长干涉，路径差必须是波长的整数倍

$\Delta l=n\lambda ,\quad n=(0,1,2,\ldots )$

因为光线是平行的，所以我们可以看到标记为θ的两个角度是相同的。这意味着我们可以使用三角函数从角度到点的距离来确定路径差

$\sin \theta ={\frac {\Delta l}{d}}$

我们还可以使用θ来计算点到屏幕中心的距离s

$\tan \theta ={\frac {s}{L}}$

对于小角度，我们可以进行以下近似

$\sin \theta \approx \tan \theta$.

因此，我们可以写

${\frac {\Delta l}{d}}={\frac {s}{L}}$

并将我们的最大相长干涉值代入，我们得到从中心线到第n个亮条纹的距离表达式

${\frac {n\lambda }{d}}={\frac {s}{L}}$

经过重新排列，得到

$s={\frac {n\lambda L}{d}},\quad n=(0,1,2,\ldots )$

让我们用前面理论中的例子来试一下。要找到基本条纹间距，只需将n设为1（这是中心条纹和一侧第一个条纹之间的间距）。

$s={\frac {\lambda L}{d}}$

$s={\frac {800\times 10^{-9}\times 5}{0.1\times 10^{-3}}}$

$s=0.04{\mbox{ m}}\,$

这与我们观察到的几乎完全一致（它只是一个近似值，所以技术上不完全精确）。为了使该公式有效，以下条件必须成立：

• 从狭缝到屏幕的距离 *L* 必须远大于狭缝间距 *d*。
• 从狭缝到条纹的角度 *θ* 必须很小。
• 如前所述，狭缝必须足够窄，以实现近乎完美的衍射。