物理数学方法/一般理论

对于线性算子$L$在$\mathbb {R}$上的格林函数是一个实函数$g$，使得$Lx=y$的解为$x=g*y$；其中$*$表示卷积。因此，$L(g*y)=y$，使得$g*y$是$L$的右逆，而$g*$是非齐次方程的特定解。

例如：$({\tfrac {d}{dt}})^{2}x+x=f$的解为$x=\sin *f=\int _{0}^{t}sin(t-\tau )f(\tau )d\tau$

这样的函数可能不存在，即使存在也可能不唯一。这种方法有效的条件需要仔细研究。然而，格林函数理论在分布理论或广义函数理论中获得了更完整和更正则的形式。

正如我们将看到的，格林函数理论提供了解微分方程的极其优雅的方法。我们希望在此以严格的基础介绍这种方法。

狄拉克δ函数

狄拉克δ函数$\delta (x)$不是通常定义的函数。然而，我们把它写成函数一样，记住定义的范围。

对于任何函数$f:\mathbb {R} \to \mathbb {R}$，我们定义

$\int _{-\infty }^{\infty }f(x)\delta (x)dx=f(0)$ 但对于每个 $\epsilon >0$,

$\int _{-\infty }^{-\epsilon }f(x)\delta (x)dx=\int _{\epsilon }^{\infty }f(x)\delta (x)dx=0$

由此可知 $\int _{-\infty }^{\infty }\delta (x)dx=1$

这些条件似乎满足了一个“函数” $\delta (x)$，当 $x\neq 0$ 时其值为零，但在 $x=0$ 时其值为“无穷大”。

近似

有几种方法可以用普通函数的序列来近似狄拉克函数。我们给出两个例子。

方波函数

方波函数 $B_{n}:\mathbb {R} \to \{0,n\}$，使得

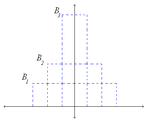
$B_{n}(x)={\begin{cases}0&|x|>{\tfrac {1}{2n}}\\n&|x|\leq {\tfrac {1}{2n}}\end{cases}}$

我们可以看到，序列 $\left\langle B_{n}\right\rangle$ 代表了对狄拉克函数的近似。

钟形曲线

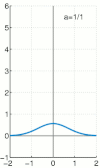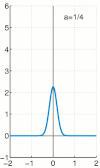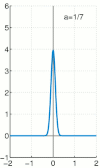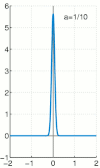
狄拉克函数也可以用无处不在的 高斯函数 来近似。

我们写 $G_{n}(x)={\frac {n}{\sqrt {\pi }}}\mathrm {e} ^{-x^{2}n^{2}}$

格林函数

考虑一个如下类型的方程 ${\mathcal {L}}u(x)=F(x)$...(1)，其中 ${\mathcal {L}}$ 是一个 *微分算子*。函数 $u,F$ 通常可能包含多个自变量，但为了清晰起见，这里我们将其写成实值函数。在大多数感兴趣的情况下，此方程可以写成

$a(x){\frac {d^{2}u}{dx^{2}}}+b(x){\frac {du}{dx}}+c(x)=F(x)$，需要在某个闭合集 $A$ 上求解 $u(x)$，其中 $a(x)$ 在 $A$ 上不为零。

现在，在物理问题中，求解方程 ${\mathcal {L}}u(x)=f(x)$ 更加方便，当 $f$ 是狄拉克函数 $f(x)=\delta (x-x_{0})$。

在这种情况下，算子 ${\mathcal {L}}$ 的解称为 **格林函数** $G(x,x_{0})$。也就是说，

${\mathcal {L}}G(x,x_{0})=\delta (x-x_{0})$

现在，根据狄拉克函数的定义，我们有 $F(x)=\int _{-\infty }^{\infty }F(x')\delta (x'-x)dx$，其中 $F(x')$ 充当狄拉克函数的“权重”。

因此，我们有， ${\mathcal {L}}u(x)=\int _{-\infty }^{\infty }F(x'){\mathcal {L}}G(x,x')dx$

请注意这里${\mathcal {L}}$ 是一个依赖于 $x$ 但不依赖于 $x'$ 的算子。因此，

${\mathcal {L}}u(x)={\mathcal {L}}\int _{-\infty }^{\infty }F(x')G(x,x')dx$。我们可以将此视为类似于 ${\mathcal {L}}$ 的反演，因此，我们写成

$u_{p}(x)=\int _{-\infty }^{\infty }F(x')G(x,x')dx$

下标 $p$ 表示我们已经找到了许多可能的解中的一个特定解。例如，考虑任何谐波解 ${\mathcal {L}}u_{h}(x)=0$。

如果我们添加 $u'(x)=u_{h}(x)+u_{p}(x)$，我们看到 $u'(x)$ 仍然是 (1) 的解。因此，我们有一类满足 (1) 的函数。

边界值问题

物理问题通常表示为算子方程 ${\mathcal {L}}u(x)=F(x)$，在闭集 $A$ 上求解 $u$，以及 **边界条件**，即 $u(x_{b})=u_{b}(x_{b})$ 对于所有 $x_{b}\in \partial A$ （$\partial A$ 是 $A$ 的边界）。

$u_{b}(x_{b})$ 是一个给定的函数，满足 ${\mathcal {L}}u_{b}(x)=0$，描述了该区域边界上解的行为。

因此，如果一个问题被描述为

${\mathcal {L}}u(x)=F(x)$，其中

$u(x_{b})=u_{b}(x_{b})$

需要在闭合集 $A$ 上求解 $u(x)$，

解可以表示为 $u_{S}(x)=u_{p}(x)+u_{b}(x)=\int _{-\infty }^{\infty }F(x')G(x,x')dx+u_{b}(x)$

从本征函数得到格林函数

考虑微分算子 ${\mathcal {L}}$ 的本征值 $\lambda _{n}$ 和对应的本征函数 $\phi _{n}$，即 ${\mathcal {L}}\phi _{n}=\lambda _{n}\phi _{n}$

不失一般性，我们假设这些本征函数是正交的。此外，我们假设它们构成一个基。

因此，我们可以写 $u(x)=\sum _{i=1}^{n}\alpha _{i}\phi _{i}$ 和 $F(x)=\sum _{i=1}^{n}\beta _{i}\phi _{i}$.

现在 ${\mathcal {L}}u(x)={\mathcal {L}}\sum _{i=1}^{n}\alpha _{i}\phi _{i}=\sum _{i=1}^{n}\alpha _{i}{\mathcal {L}}\phi _{i}=\sum _{i=1}^{n}\alpha _{i}\lambda _{i}\phi _{i}=\sum _{i=1}^{n}\beta _{i}\phi _{i}=F(x)$ 因此，$\alpha _{i}={\frac {\beta _{i}}{\lambda _{i}}}$

根据正交性的定义，$\beta _{n}=\int _{-\infty }^{\infty }F(x)\phi _{n}(x)dx=(F(x)\cdot \phi _{n}(x))$

现在，$u(x)=\sum _{i=1}^{n}\alpha _{i}\phi _{i}(x)=\sum _{i=1}^{n}{\frac {\beta _{i}}{\lambda _{i}}}\phi _{i}(x)=\sum _{i=1}^{n}{\frac {(F(x')\cdot \phi _{i}(x'))}{\lambda _{i}}}\phi _{i}$

因此，我们可以将格林函数写成 $G(x,x')=\sum _{i=1}^{n}{\frac {\phi _{i}(x)\phi _{i}(x')}{\lambda _{i}}}$