Pascal 编程/集合

本章介绍了一种新的自定义数据类型。集合是基本结构化数据类型之一。在编程中，您会经常发现某些逻辑可以用集合来建模。学习和掌握集合的使用是一项关键技能，因为您将在 Pascal 中经常遇到它们。

基础

概念

集合是（可能为空的）可区分对象的聚合。集合要么包含某个对象，要么不包含。对象作为集合的一部分也被称为该集合的元素。

假设我们知道对象“苹果”、“香蕉”和“铅笔”。集合 Fruit ≔ {“苹果”, “香蕉”} 包含对象“苹果”和“香蕉”。“铅笔”不是 Fruit 集合的成员。

数字化

当计算机需要存储和处理集合时，它实际上处理的是一系列Boolean值。 每一个Boolean值告诉我们某个元素是否属于集合。

计算机也存储一个Boolean值，用于每个不属于特定集合的对象。

Pascal 中的集合

计算机需要知道它需要保留多少个Boolean值。为了实现这一点，Pascal 中的集合需要一个序数类型作为集合的基类型。序数类型始终具有有限的允许离散值的范围，因此计算机预先知道要保留多少个Boolean值，我们最多可以期望一个集合包含多少个元素。因此，有效的集合type声明是

type
	characters = set of char;

数据类型characters的变量只能包含char值。例如，这个集合不能包含42，它是一个integer值，这些信息也不会以任何方式存储。

集合在与枚举数据类型结合使用时特别有用，您刚在上一章中学习了枚举数据类型。让我们考虑一个 Pascal 中的例子

program setDemo;

type
	skill = (cooking, cleaning, driving, videogames, eating);
	skills = set of skill;

var
	slob: skills;
begin
	slob := [videogames, eating];
end.

在这里，我们声明了一个变量slob，它表示skill枚举数据类型值的集合。在倒数第二行，我们用两个对象videogames和eating填充了我们的集合slob。方括号表示集合字面量。 [videogames, eating] 是一个集合表达式，我们将其赋值给slob变量。

集合变量slob不包含其他对象。但是，计算机仍然为该集合的每个潜在成员存储五个Boolean值。数字五是skill（集合的基类型）中的元素数量。信息cooking、cleaning和driving不属于集合slob，是显式存储的（通过适当的Boolean值false）。

检查集合

如果我们想了解某个对象是否属于集合，集合运算符in将产生计算机用来存储该信息的相应Boolean值。

program setInspection(output);
type
	skill = (cooking, cleaning, driving, videogames, eating);
	skills = set of skill;
var
	slob: skills;
begin
	slob := [videogames, eating];
	
	if videogames in slob then
	begin
		writeLn('Is she a level 45 dungeon master?');
	end;
end.

in运算符是 Pascal 的非交换运算符之一。这意味着您不能交换操作数。在RHS上，您始终需要编写一个计算为set值的表达式，而LHS必须是一个计算为该集合基类型的表达式。

尽管我们作为人类可以说42 in slob是错误的，即false，但这种比较是非法的。根据定义，slob集合只能包含skill值。

操作

到目前为止，集合可能看起来像是使用Boolean值的非常复杂的方式。集合的真正强大之处在于它的一系列不同操作，使集合成为处理两个或多个单独（但相关）Boolean值的更简单，因此更好的替代方案。

组合

在 Pascal 中，两个相同类型（相同数据类型）的集合可以组合形成一个新的相同类型集合。以下运算符可用

Pascal 中的集合运算符

名称	数学符号	源代码符号
并集	∪	+
差集	∖	-
交集	∩	*
对称差集	△	><†

_{^† 对称差集运算符仅在 EP 中定义。}

并集

在韦恩图中，两个圆圈分别代表属于任一集合或两个集合的（正）对象数量。红色区域表示并集的结果。

将两个集合合并成一个集合的结果称为并集。例如，最近我们的懒人学会了开车，现在也开车了。这可以写成

slob := slob + [driving];

现在，slob 包含它之前包含的所有对象，加上另一个集合中的所有对象，[driving]。

差集

差集作为韦恩图：右圆“减去”左圆

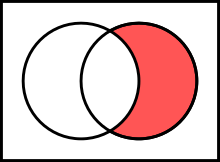
当然，可以使用差集运算符从集合中删除一组元素，在源代码中，写成 -。

slob := slob - [];

这将从第一个集合中删除第二个集合中存在的所有对象。这里，空集 ([]) 不包含任何对象，因此删除没有对象实际上对 slob 没有影响。

交集

交集作为韦恩图：重叠区域（如果有）用红色表示，代表交集

此外，您可以对集合进行交集运算。两个集合的交集定义为这两个操作数都包含的元素的集合。

program intersectionDemo;
type
	skill = (cooking, cleaning, driving, videogames, eating);
	skills = set of skill;
var
	slob, blueCollar, common: skills;
begin
	blueCollar := [cooking, cleaning, driving, eating];
	slob := [driving, videogames, eating];
	
	common := blueCollar * slob;
end.

集合 common 现在（仅）包含 driving 和 eating，因为这些是两个操作数、两个给定集合中成员的对象。

对称差集

对称差集作为韦恩图

与交集结果相反的是对称差集。它是操作数的并集，不包括两个集合中都包含的元素。

unique := blueCollar >< slob;

现在 unique 是 [cooking, cleaning, videogames]，因为这些是任一集合中的值，但不是两个集合中都包含的值。

比较

可以通过查看两个集合中的每个元素来比较两个相同类型的集合（相同的数据类型）。

Pascal 中集合的比较运算符

名称	数学符号	源代码符号
相等	=	=
不相等	≠	<>
包含	⊆	<=
包含	⊇	>=
元素	∈	in

与以前一样，所有比较运算符都计算为 Boolean 表达式。

包含

两个集合的包含意味着一个集合包含的所有对象都存在于另一个集合中。如果表达式 A <= B 计算结果为 true，则集合 A 中存在的所有对象也存在于 B 中。在韦恩图中，您会注意到一个圆圈的面积完全被另一个圆圈包围，如果不是与另一个圆圈相同的话。

关于空集的表达式始终为真，尽管没有对象需要检查。表达式 [] <= someSet 始终计算结果为 true，无论 someSet 的值是什么（它甚至可能是另一个空集）。

相等和不相等

两个集合的相等定义为 A <= B and B <= A。左边的集合中包含的所有对象都存在于右边的集合中，反之亦然。换句话说，不存在只存在于一个集合中的单个对象。不相等只是其否定。

元素

in 运算符是唯一一个不作用于两个集合而是作用于一个潜在的集合成员候选者和一个集合的集合运算符。它已在上面介绍。关于韦恩图，您可以说 in 运算符“就像”用食指指向圆圈内或圆圈外的某个点。

预定义的集合例程

基数

（在初始化之后）任何时候，集合都包含一定数量的元素。在数学中，作为集合一部分的对象的数量称为基数。可以使用函数 card（一个 EP 扩展）检索集合的基数。

emptySet := [];
writeLn(card(emptySet));

这将打印 0，因为空集中没有元素。

不幸的是，并非所有编译器都实现了 card 函数。 FPC 没有。 GPC 确实提供了一个。

全集

最初，Wirth 提出了一个函数 all

all(T)

是类型 T 的所有值的集合

例如

superwoman := all(skill);

集合 superwoman 将包含所有可用的 skill 值，cooking，cleaning，driving，videogames，eating。

不幸的是，这个提议从未进入 ISO 标准，FPC 或 GPC 也不支持该功能，或提供等效功能。唯一的替代方法是使用适当的集合构造函数（EP 扩展）：[cooking..eating] 等效于 all(skill)，前提是 cooking 是第一个 skill，而 eating 是最后一个 skill 值（指的是这些项目在 skill 数据类型声明期间的列出顺序）。

包含和排除

虽然没有标准化，但很方便的是 BP 对 include 和 exclude 过程的定义。这些是针对非常频繁的集合操作的简写。

这些过程允许您快速从一个集合中添加或删除一个对象。

include(recognizedLetters, 'Z');

与以下相同

recognizedLetters := recognizedLetters + ['Z'];

但您不需要两次键入集合名称以及其他所有内容，从而减少了键入错误的可能性。同样地，

exclude(primeSieve, 4);

将执行与以下相同的操作

primeSieve := primeSieve - [4];

FPC 和 GPC 都支持这些方便的例程，这些例程实际上在所有情况下都作为编译器内在函数实现，而不是实际的 procedure。

中间用法

集合文字

有效地声明集合是在处理集合时一项必备技能。重要的是要理解，集合仅存储一个对象是否属于一个集合的信息。集合 ['A', 'A', 'A'] 与 ['A'] 相同。多次指定 'A' 不会使其“更多”地成为该集合的一部分。

此外，没有必要以任何特定顺序列出所有成员。['X', 'Z', 'Y'] 与 ['X', 'Y', 'Z'] 一样是可以接受的。从数学角度讲，集合是无序的。 Pascal 的要求 是集合的基本数据类型必须是序数类型，这纯粹是一个技术要求。但是，出于可读性的原因，通常将元素按升序排列是有意义的。

EP 标准为您提供了 set 文字的简洁表示法，其中包含一系列连续的值。与其编写 [7, 8, 9, 11, 12, 13]，您也可以编写范围，例如 [7..9, 11..13]，其计算结果与上述值相同。当然，所有数字也可以是变量，或者更一般地说是表达式。

集合文字始终是关于哪些对象存在于集合中的肯定陈述。如果我们想要一个集合，其中包含 integer 值，范围为 0 到 10，不包括 3，5 和 7，但不想完全写出这个集合（即，作为 [0, 1, 2, 4, 6, 8, 9, 10]），您可以编写 [0..2, 4, 6, 8..10] 或表达式 [0..10] - [3, 5, 7]。后者可能更容易理解哪些对象存在于最终集合中，而哪些对象不存在。

内存限制

虽然 set of integer 是合法的，并且符合所有 Pascal 标准，但许多编译器不支持这种大型集合。根据定义，一个 set of integer 可以包含（最多）范围内所有值 -maxInt..maxInt。这是一个很大的数字（尝试 writeLn(maxInt) 或阅读您的编译器文档以了解该值）。在 64 位平台上，该值（通常）为 2⁶³−1，即 9,223,372,036,854,775,808。截至 2020 年，许多计算机如果尝试保存这么多 Boolean 值，将很快耗尽主内存。

因此，BP 限制了允许的集合基本类型。在 BP 中，基本类型最大和最小值的序数值必须在范围内 0..255。值 255 是 2⁸−1。截至 3.2.0 版，FPC 设置了相同的限制。

GPC 允许定义超过 2⁸ 个元素的 set，尽管需要进行一些配置：您需要指定 ‑‑setlimit 命令行参数或在源代码中使用经过专门设计的注释

program largeSetDemo;
{$setLimit=2147483647} // this is 2³¹ − 1
type
	// 1073741823 is 2³⁰ − 1
	characteristicInteger = -1073741823..1073741823;
	integers = set of characteristicInteger;
var
	manyManyIntegers: integers;
begin
	manyManyIntegers := [];
	include(manyManyIntegers, 1073741823);
end.

这将指示 GPC set of characteristicInteger 只能存储最多这么多 characteristicInteger 值。

循环

既然您已经了解了枚举数据类型和集合，您将面临着处理越来越多的数据。Pascal 与许多其他编程语言一样，支持一种称为*循环*的语言结构。

特征

循环是（可能为空的）语句序列，根据Boolean值，一遍又一遍地重复，甚至从未执行。语句序列称为*循环体*。*循环头*包含（可能隐式）一个Boolean表达式，用于确定是否执行循环体。每次运行循环体时，都进行一次*迭代*。

*循环*一词起源于早期的计算机模型，这些模型需要通过穿孔纸带输入（“加载”）程序。如果该纸带的一部分需要多次处理，则将该部分纸带剪断、弯曲并暂时固定，形成一个*物理循环*。值得庆幸的是，计算机技术的进步使处理重复代码变得更加方便。

Pascal（以及许多其他编程语言）区分两种循环组

• 计数循环，此处介绍，以及
• 条件循环，将在后面的章节中介绍。

计数循环的共同点是，在运行第一次迭代之前，只需评估循环头，就可以确定循环体将执行*多少次*。另一方面，条件循环是基于中止条件，即一个Boolean表达式。除了无限循环之外，没有办法提前确定条件循环将执行多少次（多少次迭代），除非彻底（数学地）分析循环体和循环头，甚至可能考虑循环之外的情况。

计数循环

计数循环并不一定*计数*一个数量。它们之所以得名，是因为它们使用一个变量，一个*计数变量*。这个任何序数数据类型的变量（实际上）为每次迭代分配一个数字。

计数循环由保留字for引入。

program forLoopDemo(output);
var
	i: integer;
begin
	for i := 1 to 10 do // loop head
	begin               // ┐
		writeLn(i:3);   // ┝ loop body
	end;                // ┘
end.

在for之后，紧跟一个专门设计的对计数变量的赋值。

计数变量的范围

1 to 10（使用辅助保留字to）表示计数变量i在执行循环体时将采用的值的*范围*。 1 和 10 都是具有计数变量数据类型的*表达式*，这意味着也可能出现变量或更复杂的表达式，而不仅仅是如所示的常量文字。

此范围*类似于*一个set。它可能为空：范围5 to 4是一个*空*范围，因为在 5*到*并包括 4之间没有值。因此，计数变量不会从该空范围分配任何值，因为根本没有可用的值，并且循环体*永远不会*执行。但是，范围8 to 8恰好包含一个值，即 8。

在第一次迭代期间，相应的计数变量（此处为 i）将具有给定范围内的第一个值，即*起始值*，在上面的示例中，这是值 1。在随后的迭代中，变量 i 的值为 2，依此类推，直到并包括给定范围内的*最终值*，此处为 10。

计数变量的不可变性

在循环体内部不需要实际使用计数变量，但如果您*仅*获取其当前值，则可以*使用*它：在for循环的循环体内部，禁止对计数变量赋值。禁止的赋值包括但不限于将计数变量置于:=的LHS，还包括read/readLn，它们不能使用计数变量。篡改计数变量是被禁止的，因为循环头将有效地使用succ(i) 来获取下一次迭代的值。循环头*隐式*包含Boolean表达式 计数变量 ≠ 最终值。如果计数变量 被操纵，则此条件*可能*永远不会满足，从而破坏了for循环的特性。通过阻止程序员进行任何赋值，可以预先确保不会意外或故意创建这样的无限循环。

反向

Pascal 还允许使用保留字downto（而不是to）以反向方向使用for循环。

program downtoDemo(output);
var
	c: char;
begin
	for c := 'Z' downto 'B' do
	begin
		write(c, ' ');
	end;
	writeLn('A');
end.

此处，范围是'Z'*向下*并包括到 'B'。循环的终止条件仍然是 计数变量 ≠ 最终值，但在这种情况下，计数变量 c 在每次迭代结束时（循环体执行完毕后）变为 pred(c)（而不是 succ）。

集合上的循环

EP 允许迭代离散聚合，例如集合。如果您有一个需要应用于聚合的每个值的例程，这将特别有用。以下是一个示例，用于演示该原理。

program forInDemo(output);
var
	c: char;
	vowels: set of char;
begin
	vowels := ['A', 'E', 'I', 'O', 'U'];
	
	for c in vowels do
	begin
		writeLn(c);
	end;
end.

现在您又看到了单词in，但在这种情况下，c in vowels 不是一个表达式。in 的数据类型限制仍然有效：在RHS 上，给出了一个聚合表达式，而在LHS 上，在这种情况下，是一个*变量*，它具有聚合的数据类型。这个变量将在每次处理迭代时被分配从给定聚合中得到的每个值。

由于RHS 只需要一个*表达式*，而不是一个变量，因此您可以进一步缩短示例。

    for c in ['A', 'E', 'I', 'O', 'U'] do

请注意，与上面的计数循环不同，您不应该对循环变量被分配值的顺序做出任何假设。它可能是按升序、降序或完全混合的“顺序”，但具体顺序是“实现定义的”，即它取决于使用的编译器。编译器的附带文档解释了for … in 循环 的处理顺序。

任务

集合表达式fruit - fruit 计算结果是什么值？

此表达式将评估为一个空集，因为差运算符会从前一个集合中“移除”后一个集合包含的所有对象。这里，我们两次引用同一个集合，所以两个操作数相等，实际上将表达式简化为“移除同一个集合中的所有对象”。不用说，写出这样的表达式毫无意义，因为我们已经知道它的结果，但它仍然是允许的。

来源

备注