实用电子学/逻辑/布尔恒等式

有几个定律可以用来简化或修改布尔表达式。此页面将解释它们，此页面将列出它们以便于参考。

公理

公理是被认为是显而易见的命题，因此不需要被证明 - 事实上它们不能被证明，因为它们被定义为是通过代数结构为真。它们通过定义两个值 1 和 0 以及三个运算符 AND、OR、FLO 和 NOT，构成了布尔代数的其余部分的基础。

	公理	公理对偶
1	${\mbox{If }}X\neq 1,\,X=0$	${\mbox{If }}X\neq 0,\,X=1$
2	${\mbox{If }}X=0,\,{\overline {X}}=1$	${\mbox{If }}X=1,\,{\overline {X}}=0$
3	$0\cdot 0=0$	$1+1=1\,$
4	$1\cdot 1=1$	$0+0=0\,$
5	$1\cdot 0=0\cdot 0=0$	$1+0=0+1=1\,$

德摩根定律

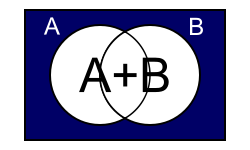
德摩根定律是用于分组或取消分组逻辑语句的非常强大的工具。它基本上表明逻辑函数 AND 或 OR 可以用另一个替换，前提是对等式进行某些更改。它通常表示为两个不同的恒等式。第一个是以下内容

{\overline {A+B}}={\overline {A}}\cdot {\overline {B}}

一开始，可能不清楚如何找到这个结果，但是如果你看一下左边的第一个维恩图，就很清楚了。想象一个名为 X 的变量，它由以下定义

X={\overline {A+B}}

这意味着 X 不在组 A 或 B 中，因此它必须在蓝色区域。现在，这等同于说 X 不在 A 中并且不在 B 中。这意味着我们也可以将 X 定义为

X={\overline {A}}\cdot {\overline {B}}

这也可以通过绘制真值表来看到：从表的每一端开始，我们可以看到这两个表给出了相同的结果

A	B	A+B	¬(A+B)	¬A•¬B	¬B	¬A
0	0	0	1	1	1	1
0	1	1	0	0	0	1
1	0	1	0	0	1	0
1	1	1	0	0	0	0

第二个表达式基本上相同，但交换了符号

{\overline {A\cdot B}}={\overline {A}}+{\overline {B}}

如果我们对X再进行同样的操作，我们会发现X一定 **不** 在A **和** B中。因此，X一定在浅蓝色、深蓝色或红色区域，而不是在中心。现在我们可以说，X要么不在A中，要么不在B中，要么两者都不在。这与说X **不** 在A中 **或** **不** 在B中是一样的（使用逻辑意义上的“或”）。因此，

X={\overline {A}}+{\overline {B}}

同样，这可以用真值表来表示

A	B	A•B	¬(A•B)	¬A+¬B	¬B	¬A
0	0	0	1	1	1	1
0	1	0	1	1	0	1
1	0	0	1	1	1	0
1	1	1	0	0	0	0

记住上面给出的定律的一个简单方法是：**“分割线条，改变符号”。** 通过这两个规则，可以证明任何逻辑语句都可以通过以下方法改变

对表达式中的所有项取反
将所有AND改为OR，将所有OR改为AND
对结果取反

另见

以上定律的总结