定义. (伯努利试验) 一个伯努利试验 两个
备注。
'成功'和'失败'仅仅作为标签,即我们可以将实验中的任何一个结果定义为'成功'。
定义. (伯努利试验的独立性) 令 S i {\displaystyle S_{i}} { i th Bernoulli trial is a success } , i = 1 , 2 , … {\displaystyle \{i{\text{th Bernoulli trial is a success}}\},\quad i=1,2,\dotsc } [ 1] S 1 , S 2 , … {\displaystyle S_{1},S_{2},\dotsc } 独立 独立
示例. 如果我们将抛硬币的结果解释为'正面朝上'和'反面朝上',那么抛硬币就是一个伯努利试验。
练习。
备注。
我们通常将抛硬币的结果解释为'正面朝上'和'反面朝上'。
考虑 n {\displaystyle {\color {blue}n}} p {\displaystyle {\color {darkgreen}p}} P ( { r successes in n trials } ) {\displaystyle \mathbb {P} (\{{\color {darkgreen}r}{\text{ successes in }}{\color {blue}n}{\text{ trials}}\})}
设 S i {\displaystyle S_{i}} { i th Bernoulli trial is a success } , i = 1 , 2 , … {\displaystyle \{i{\text{th Bernoulli trial is a success}}\},\quad i=1,2,\dotsc } r {\displaystyle {\color {darkgreen}r}} n {\displaystyle {\color {blue}n}} S ⋯ S ⏟ r successes F ⋯ F ⏞ n − r failures {\displaystyle {\color {darkgreen}\underbrace {S\cdots S} _{r{\text{ successes}}}}{\color {red}\overbrace {F\cdots F} ^{{\color {blue}n}-{\color {darkgreen}r}{\text{ failures}}}}} P ( S 1 ∩ ⋯ S r ∩ S r + 1 c ∩ ⋯ ∩ S n c ) = indpt. P ( S 1 ) ⋯ P ( S r ) P ( S r + 1 c ) ⋯ P ( S n c ) = p r ( 1 − p ) n − r {\displaystyle \mathbb {P} ({\color {darkgreen}S_{1}\cap \dotsb S_{r}}\cap {\color {red}S_{r+1}^{c}\cap \dotsb \cap S_{\color {blue}n}^{c}}){\overset {\text{ indpt. }}{=}}{\color {darkgreen}\mathbb {P} (S_{1})\dotsb \mathbb {P} (S_{r})}{\color {red}\mathbb {P} (S_{r+1}^{c})\cdots \mathbb {P} (S_{\color {blue}n}^{c})}={\color {darkgreen}p^{r}}{\color {red}(1-{\color {darkgreen}p})^{{\color {blue}n}-{\color {darkgreen}r}}}} [ 2] r {\displaystyle {\color {darkgreen}r}} 相同 ( n r ) {\displaystyle {\binom {\color {blue}n}{\color {darkgreen}r}}} [ 3] P ( { r successes in n trials } ) = ( n r ) p r ( 1 − p ) n − r . {\displaystyle \mathbb {P} (\{{\color {darkgreen}r}{\text{ successes in }}{\color {blue}n}{\text{ trials}}\})={\binom {\color {blue}n}{\color {darkgreen}r}}{\color {darkgreen}p}^{\color {darkgreen}r}{\color {red}(1-{\color {darkgreen}p})^{{\color {blue}n}-{\color {darkgreen}r}}}.} 二项分布
定义。 (二项分布)
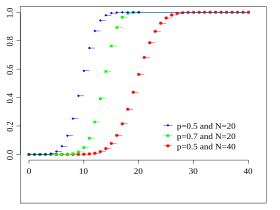
Binom ( 20 , 0.5 ) , Binom ( 20 , 0.7 ) {\displaystyle {\color {blue}\operatorname {Binom} (20,0.5)},{\color {green}\operatorname {Binom} (20,0.7)}} Binom ( 40 , 0.5 ) {\displaystyle {\color {red}\operatorname {Binom} (40,0.5)}} 随机变量 X {\displaystyle X} 二项分布 n {\displaystyle {\color {blue}n}} p {\displaystyle {\color {darkgreen}p}} X ∼ Binom ( n , p ) {\displaystyle X\sim \operatorname {Binom} ({\color {blue}n},{\color {darkgreen}p})} f ( x ; n , p ) = ( n x ) p x ( 1 − p ) n − x , x ∈ supp ( X ) = { 0 , 1 , 2 , … , n } . {\displaystyle f({\color {darkgreen}x};{\color {blue}n},{\color {darkgreen}p})={\binom {\color {blue}n}{\color {darkgreen}x}}{\color {darkgreen}p^{x}}{\color {red}(1-{\color {darkgreen}p})^{{\color {blue}n}-{\color {darkgreen}x}}},\quad {\color {darkgreen}x}\in \operatorname {supp} (X)=\{0,1,2,\dotsc ,{\color {blue}n}\}.}
Binom ( 20 , 0.5 ) , Binom ( 20 , 0.7 ) {\displaystyle {\color {blue}\operatorname {Binom} (20,0.5)},{\color {green}\operatorname {Binom} (20,0.7)}} Binom ( 40 , 0.5 ) {\displaystyle {\color {red}\operatorname {Binom} (40,0.5)}}
伯努利分布是 二项式
定义。 (伯努利分布)
Ber ( 0.8 ) , Ber ( 0.2 ) {\displaystyle {\color {red}\operatorname {Ber} (0.8)},{\color {blue}\operatorname {Ber} (0.2)}} Ber ( 0.5 ) {\displaystyle {\color {darkgreen}\operatorname {Ber} (0.5)}} 一个随机变量 X {\displaystyle X} p {\displaystyle {\color {darkgreen}p}} 伯努利分布 X ∼ Ber ( p ) {\displaystyle X\sim \operatorname {Ber} ({\color {darkgreen}p})} f ( x ; p ) = p x ( 1 − p ) 1 − x , x ∈ supp ( X ) = { 0 , 1 } . {\displaystyle f({\color {darkgreen}x};{\color {darkgreen}p})={\color {darkgreen}p^{x}}{\color {red}(1-{\color {darkgreen}p})^{1-{\color {darkgreen}x}}},\quad {\color {darkgreen}x}\in \operatorname {supp} (X)=\{0,1\}.}
Ber ( 1 ) , Ber ( 0.8 ) , Ber ( 0.5 ) {\displaystyle {{\color {blue}\operatorname {Ber} (1)},\color {red}\operatorname {Ber} (0.8)},{\color {darkorange}\operatorname {Ber} (0.5)}} Ber ( 0.3 ) {\displaystyle {\color {darkgreen}\operatorname {Ber} (0.3)}}
备注。
Ber ( p ) = Binom ( 1 , p ) {\displaystyle \operatorname {Ber} ({\color {darkgreen}p})=\operatorname {Binom} (1,{\color {darkgreen}p})} 这是一个伯努利 伯努利
泊松分布可以被看作是二项分布的“极限情况”。
考虑 n {\displaystyle {\color {blue}n}} p = λ / n {\displaystyle {\color {darkgreen}p}=\lambda /{\color {blue}n}} P ( r successes in n trials ) = ( n r ) ( λ / n ) r ( 1 − λ / n ) n − r . {\displaystyle \mathbb {P} ({\color {darkgreen}r}{\text{ successes in }}{\color {blue}n}{\text{ trials}})={\binom {\color {blue}n}{\color {darkgreen}r}}{\color {darkgreen}(\lambda /{\color {blue}n})^{r}}{\color {red}(1-\lambda /{\color {blue}n})^{{\color {blue}n}-{\color {darkgreen}r}}}.}
After that, consider an unit time interval, with (positive) occurrence rate λ {\displaystyle \lambda } mean λ {\displaystyle \lambda } n {\displaystyle {\color {blue}n}} 1 / n {\displaystyle 1/{\color {blue}n}} n {\displaystyle {\color {blue}n}} large p {\displaystyle {\color {darkgreen}p}} relatively small rare events exactly one rare event p = λ / n {\displaystyle {\color {darkgreen}p}=\lambda /{\color {blue}n}} n {\displaystyle {\color {blue}n}} [ 4] p = λ / n {\displaystyle {\color {darkgreen}p}=\lambda /{\color {blue}n}} Binom ( n , λ / n ) {\displaystyle \operatorname {Binom} {({\color {blue}n},\lambda /{\color {blue}n})}} rare event P ( r successes in n trials ⏟ r rare events in the unit time ) = ( n r ) ( λ / n ) r ( 1 − λ / n ) n − r = n ( n − 1 ) ⋯ ( n − r + 1 ) r ! ( λ r / n r ) ( 1 − λ / n ) n − r = ( λ r / r ! ) ( 1 − 1 / n ⏟ → 0 as n → ∞ ) ⋯ ( 1 − ( r − 1 ) / n ⏟ → 0 as n → ∞ ) ⏞ → 1 as n → ∞ ( 1 − λ / n ) n − r ⏞ → n as n → ∞ ⏟ → e − λ as n → ∞ → e − λ λ r / r ! as n → ∞ . {\displaystyle {\begin{aligned}\mathbb {P} (\underbrace {{\color {darkgreen}r}{\text{ successes in }}{\color {blue}n}{\text{ trials}}} _{{\color {darkgreen}r}{\text{ rare events in the unit time}}})&={\binom {\color {blue}n}{\color {darkgreen}r}}{\color {darkgreen}(\lambda /{\color {blue}n})^{r}}{\color {red}(1-\lambda /{\color {blue}n})^{{\color {blue}n}-{\color {darkgreen}r}}}\\&={\frac {{\color {blue}n}({\color {blue}n}-1)\dotsb ({\color {blue}n}-{\color {darkgreen}r}+1)}{{\color {darkgreen}r}!}}(\lambda ^{\color {darkgreen}r}/{\color {blue}n}^{\color {darkgreen}r})(1-\lambda /{\color {blue}n})^{{\color {blue}n}-{\color {darkgreen}r}}\\&=(\lambda ^{\color {darkgreen}r}/{\color {darkgreen}r}!)\overbrace {(1-\underbrace {1/{\color {blue}n}} _{\to 0{\text{ as }}n\to \infty })\dotsb {\big (}1-\underbrace {({\color {darkgreen}r-1})/{\color {blue}n}} _{\to 0{\text{ as }}n\to \infty }{\big )}} ^{\to 1{\text{ as }}n\to \infty }\underbrace {(1-\lambda /{\color {blue}n})^{\overbrace {{\color {blue}n}-{\color {darkgreen}r}} ^{\to n{\text{ as }}n\to \infty }}} _{\to e^{-\lambda }{\text{ as }}n\to \infty }\\&\to e^{-\lambda }\lambda ^{\color {darkgreen}r}/{\color {darkgreen}r}!{\text{ as }}n\to \infty .\end{aligned}}} Poisson distribution Poisson limit theorem Poisson distribution
定义。 (泊松分布)
Pois ( 1 ) , Pois ( 4 ) {\displaystyle {\color {darkorange}\operatorname {Pois} (1)},{\color {purple}\operatorname {Pois} (4)}} Pois ( 10 ) {\displaystyle {\color {royalblue}\operatorname {Pois} (10)}} 如果随机变量 X {\displaystyle X} λ {\displaystyle \lambda } 泊松分布 X ∼ Pois ( λ ) {\displaystyle X\sim \operatorname {Pois} (\lambda )} f ( x ; λ ) = e − λ λ x / x ! , x ∈ supp ( X ) = { 0 , 1 , 2 , … } . {\displaystyle f({\color {darkgreen}x};\lambda )=e^{-\lambda }\lambda ^{\color {darkgreen}x}/{\color {darkgreen}x}!,\quad {\color {darkgreen}x}\in \operatorname {supp} (X)=\{0,1,2,\dotsc \}.}
Pois ( 1 ) , Pois ( 4 ) {\displaystyle {\color {darkorange}\operatorname {Pois} (1)},{\color {purple}\operatorname {Pois} (4)}} Pois ( 10 ) {\displaystyle {\color {royalblue}\operatorname {Pois} (10)}}
备注。
因此,泊松分布可用于近似大的 n {\displaystyle {\color {blue}n}} p = λ / n {\displaystyle {\color {darkgreen}p}=\lambda /{\color {blue}n}}
考虑一个独立伯努利试验序列,其成功概率为 p {\displaystyle {\color {darkgreen}p}} P ( { x failures before first success } ) {\displaystyle \mathbb {P} (\{{\color {red}x}{\text{ failures before first success}}\})} F ⋯ F ⏟ x failures S , {\displaystyle {\color {red}\underbrace {F\cdots F} _{{\color {red}x}{\text{ failures}}}}{\color {darkgreen}S},} P ( { x failures before first success } ) = ( 1 − p ) x p , x ∈ supp ( X ) = { 0 , 1 , 2 , … } {\displaystyle \mathbb {P} (\{{\color {red}x}{\text{ failures before first success}}\})={\color {red}(1-{\color {darkgreen}p})^{x}}{\color {darkgreen}p},\quad {\color {red}x}\in \operatorname {supp} (X)=\{0,1,2,\dotsc \}} [ 5] 几何分布
定义。 (几何分布)
Geo ( 0.2 ) , Geo ( 0.5 ) {\displaystyle {\color {green}\operatorname {Geo} (0.2)},{\color {blue}\operatorname {Geo} (0.5)}} Geo ( 0.8 ) {\displaystyle {\color {red}\operatorname {Geo} (0.8)}} 如果随机变量 X {\displaystyle X} p {\displaystyle {\color {darkgreen}p}} 几何分布 X ∼ Geo ( p ) {\displaystyle X\sim \operatorname {Geo} ({\color {darkgreen}p})} f ( x ; p ) = ( 1 − p ) x p , x ∈ supp ( X ) = { 0 , 1 , 2 , … } . {\displaystyle f({\color {red}x};{\color {darkgreen}p})={\color {red}(1-{\color {darkgreen}p})^{x}}{\color {darkgreen}p},\quad {\color {red}x}\in \operatorname {supp} (X)=\{0,1,2,\dotsc \}.}
Geo ( 0.2 ) , Geo ( 0.5 ) {\displaystyle {\color {green}\operatorname {Geo} (0.2)},{\color {blue}\operatorname {Geo} (0.5)}} Geo ( 0.8 ) {\displaystyle {\color {red}\operatorname {Geo} (0.8)}}
备注。
从 f ( 0 ; p ) {\displaystyle f(0;{\color {darkgreen}p})} x {\displaystyle {\color {red}x}} p , ( 1 − p ) p , ( 1 − p ) 2 p , … {\displaystyle {\color {darkgreen}p},{\color {red}(1-{\color {darkgreen}p})}{\color {darkgreen}p},{\color {red}(1-{\color {darkgreen}p})^{2}}{\color {darkgreen}p},\dotsc } 等比数列 几何
另一种定义是,概率质量函数为 ( 1 − p ) x − 1 p {\displaystyle (1-p)^{x-1}p} P ( { x trials before first success } ) {\displaystyle \mathbb {P} (\{x{\text{ trials before first success}}\})} supp ( X ) = { 1 , 2 , … } {\displaystyle \operatorname {supp} (X)=\{1,2,\dotsc \}}
证明。 P ( X > m + n | X ≥ m ) = def P ( X > m + n ∩ X ≥ m ) ⏞ = X > m + n P ( X ≥ m ) = def p ( ( 1 − p ) m + n + 1 + ( 1 − p ) m + n + 2 + ⋯ ) p ( ( 1 − p ) m + ( 1 − p ) m + 1 + ⋯ ) = ( 1 − p ) m + n + 1 / ( 1 − ( 1 − p ) ) ( 1 − p ) m / ( 1 − ( 1 − p ) ) by geometric series formula = ( 1 − p ) n + 1 ⋅ p p = p ⋅ ( 1 − p ) n + 1 1 − ( 1 − p ) = p ( ( 1 − p ) n + 1 + ( 1 − p ) n + 2 + ⋯ ) by geometric series formula = def P ( X > n ) since X > n ⇔ X = n + 1 , n + 2 , … . {\displaystyle {\begin{aligned}\mathbb {P} (X>m+n|X\geq m)&{\overset {\text{ def }}{=}}{\frac {\mathbb {P} (\overbrace {X>m+n\cap X\geq m)} ^{=X>m+n}}{\mathbb {P} (X\geq m)}}\\&{\overset {\text{ def }}{=}}{\frac {{\cancel {p}}\left((1-p)^{m+n+1}+(1-p)^{m+n+2}+\dotsb \right)}{{\cancel {p}}\left((1-p)^{m}+(1-p)^{m+1}+\dotsb \right)}}\\&={\frac {(1-p)^{{\cancel {m}}+n+1}{\cancel {/{\big (}1-(1-p){\big )}}}}{{\cancel {(1-p)^{m}}}{\cancel {/{\big (}1-(1-p){\big )}}}}}&{\text{by geometric series formula}}\\&=(1-p)^{n+1}\cdot {\frac {\color {darkgreen}p}{\color {blue}p}}\\&={\color {darkgreen}p}\cdot {\frac {(1-p)^{n+1}}{\color {blue}1-(1-p)}}\\&={\color {darkgreen}p}\left((1-p)^{n+1}+(1-p)^{n+2}+\dotsb \right)&{\text{by geometric series formula}}\\&{\overset {\text{ def }}{=}}\mathbb {P} (X>n)&{\text{since }}X>n\Leftrightarrow X=n+1,n+2,\dotsc .\\\end{aligned}}}
特别是, X > m + n ∩ X ≥ m = X > m + n {\displaystyle X>m+n\cap X\geq m=X>m+n} X > m + n ⏟ X = m + n + 1 , m + n + 2 , … ⊊ X ≥ m ⏟ X = m , m + 1 , … {\displaystyle \underbrace {X>m+n} _{X=m+n+1,m+n+2,\dotsc }\subsetneq \underbrace {X\geq m} _{X=m,m+1,\dotsc }} ◻ {\displaystyle \Box }
Consider a sequence of independent Bernoulli trials with success probability p {\displaystyle {\color {darkgreen}p}} P ( { x failures before k th success } ) {\displaystyle \mathbb {P} (\{{\color {red}x}{\text{ failures before }}{\color {darkgreen}k}{\text{th success}}\})} F ⋯ F ⏟ x 1 failures S F ⋯ F ⏟ x 2 failures S ⋯ F ⋯ F ⏟ x k failures ⏞ x + k − 1 trials S ⏞ k th success , x 1 + x 2 + ⋯ + x k = x , {\displaystyle \overbrace {{\color {red}\underbrace {F\cdots F} _{x_{1}{\text{ failures}}}}{\color {darkgreen}S}{\color {red}\underbrace {F\cdots F} _{x_{2}{\text{ failures}}}}{\color {darkgreen}S}\cdots {\color {red}\underbrace {F\cdots F} _{x_{k}{\text{ failures}}}}} ^{{\color {red}x}+{\color {darkgreen}k}-1{\text{ trials}}}{\color {darkgreen}\overbrace {S} ^{k{\text{th success}}}},\quad {\color {red}x_{1}}+{\color {red}x_{2}}+\dotsb +{\color {red}x_{k}}={\color {red}x},} P ( { x failures before k th success } ) = ( 1 − p ) x p k , x ∈ supp ( X ) = { 0 , 1 , 2 , … } . {\displaystyle \mathbb {P} (\{{\color {red}x}{\text{ failures before }}{\color {darkgreen}k}{\text{th success}}\})={\color {red}(1-{\color {darkgreen}p})^{x}}{\color {darkgreen}p^{k}},\quad {\color {red}x}\in \operatorname {supp} (X)=\{0,1,2,\dotsc \}.} x {\displaystyle {\color {red}x}} k − 1 {\displaystyle {\color {darkgreen}k}-1} k {\displaystyle {\color {darkgreen}k}} same ( x + k − 1 x ) {\displaystyle {\binom {{\color {red}x}+{\color {darkgreen}k}-1}{\color {red}x}}} ( x + k − 1 k − 1 ) {\displaystyle {\binom {{\color {red}x}+{\color {darkgreen}k}-1}{{\color {green}k}-1}}} [ 6] P ( { x failures before k th success } ) = ( x + k − 1 x ) ( 1 − p ) x p k , x ∈ supp ( X ) = { 0 , 1 , 2 , … } . {\displaystyle \mathbb {P} (\{{\color {red}x}{\text{ failures before }}{\color {darkgreen}k}{\text{th success}}\})={\binom {{\color {red}x}+{\color {darkgreen}k}-1}{\color {red}x}}{\color {red}(1-{\color {darkgreen}p})^{x}}{\color {darkgreen}p^{k}},\quad {\color {red}x}\in \operatorname {supp} (X)=\{0,1,2,\dotsc \}.} negative binomial distribution
定义. (负二项分布)
NB ( 10 , 0.9 ) , NB ( 10 , 0.8 ) , NB ( 10 , 0.5 ) {\displaystyle {\color {darkblue}\operatorname {NB} (10,0.9)},{\color {red}\operatorname {NB} (10,0.8)},{\color {darkorange}\operatorname {NB} (10,0.5)}} NB ( 10 , 0.3 ) {\displaystyle {\color {darkgreen}\operatorname {NB} (10,0.3)}} 随机变量 X {\displaystyle X} 负二项分布 成功概率 p {\displaystyle {\color {darkgreen}p}} X ∼ NB ( k , p ) {\displaystyle X\sim \operatorname {NB} ({\color {darkgreen}k,p})} f ( x ; k , p ) = ( x + k − 1 x ) ( 1 − p ) x p k , x ∈ supp ( X ) = { 0 , 1 , 2 , … } . {\displaystyle f({\color {red}x};{\color {darkgreen}k,p})={\binom {{\color {red}x}+{\color {darkgreen}k}-1}{\color {red}x}}{\color {red}(1-{\color {darkgreen}p})^{x}}{\color {darkgreen}p^{k}},\quad {\color {red}x}\in \operatorname {supp} (X)=\{0,1,2,\dotsc \}.}
NB ( 10 , 0.9 ) , NB ( 10 , 0.8 ) , NB ( 10 , 0.5 ) {\displaystyle {\color {royalblue}\operatorname {NB} (10,0.9)},{\color {red}\operatorname {NB} (10,0.8)},{\color {darkorange}\operatorname {NB} (10,0.5)}} NB ( 10 , 0.3 ) {\displaystyle {\color {darkgreen}\operatorname {NB} (10,0.3)}}
考虑从总体大小为 N {\displaystyle N} n {\displaystyle n} K {\displaystyle K} N − K {\displaystyle N-K} P ( { k type 1 objects are found when n objects are drawn from N objects } ) = ( K k ) ⏟ type 1 ( N − K n − k ) ⏞ another type / ( N n ) ⏟ all outcomes , k ∈ { max { n − N + K , 0 } , … , min { K , n } } {\displaystyle \mathbb {P} (\{k{\text{ type 1 objects are found when }}n{\text{ objects are drawn from }}N{\text{ objects}}\})=\underbrace {\binom {K}{k}} _{\text{type 1}}\overbrace {\binom {N-K}{n-k}} ^{\text{another type}}{\bigg /}\underbrace {\binom {N}{n}} _{\text{all outcomes}},\quad k\in {\big \{}\max\{n-N+K,0\},\dotsc ,\min {\{K,n\}}{\big \}}} [ 7]
( K k ) {\displaystyle {\binom {K}{k}}} K {\displaystyle K} k {\displaystyle k} ( N − K n − k ) {\displaystyle {\binom {N-K}{n-k}}} N − K {\displaystyle N-K} n − k {\displaystyle n-k} ( N n ) {\displaystyle {\binom {N}{n}}} N {\displaystyle N} n {\displaystyle n} 这是一个遵循 超几何分布
定义。 (超几何分布)
HypGeo ( 500 , 50 , 100 ) , HypGeo ( 500 , 60 , 200 ) {\displaystyle {\color {blue}\operatorname {HypGeo} (500,50,100)},{\color {darkgreen}\operatorname {HypGeo} (500,60,200)}} HypGeo ( 500 , 70 , 300 ) {\displaystyle {\color {red}\operatorname {HypGeo} (500,70,300)}} 随机变量 X {\displaystyle X} 超几何分布 K {\displaystyle K} N − K {\displaystyle N-K} n {\displaystyle n} X ∼ HypGeo ( N , K , n ) {\displaystyle X\sim \operatorname {HypGeo} (N,K,n)} f ( k ; N , K , n ) = ( K k ) ( N − K n − k ) / ( N n ) , k ∈ supp ( X ) = { max { n − N + K , 0 } , … , min { K , n } } . {\displaystyle f(k;N,K,n)={\binom {K}{k}}{\binom {N-K}{n-k}}{\bigg /}{\binom {N}{n}},\quad k\in \operatorname {supp} (X)={\big \{}\max\{n-N+K,0\},\dotsc ,\min {\{K,n\}}{\big \}}.}
HypGeo ( 500 , 50 , 100 ) , HypGeo ( 500 , 60 , 200 ) {\displaystyle {\color {blue}\operatorname {HypGeo} (500,50,100)},{\color {darkgreen}\operatorname {HypGeo} (500,60,200)}} HypGeo ( 500 , 70 , 300 ) {\displaystyle {\color {red}\operatorname {HypGeo} (500,70,300)}}
备注。
概率质量函数有点类似于 超几何 [ 8] 超几何
这种类型的分布是所有具有有限支撑的离散分布的推广,例如伯努利分布和超几何分布。
这种类型分布的另一个特例是 离散均匀分布 连续均匀分布
定义。 (有限离散分布) 随机变量 X {\displaystyle X} x = ( x 1 , … , x n ) T {\displaystyle \mathbf {x} =(x_{1},\dotsc ,x_{n})^{T}} p = ( p 1 , … , p n ) T , p 1 , … , and p n ≥ 0 , p 1 + ⋯ + p n = 1 {\displaystyle \mathbf {p} =(p_{1},\dotsc ,p_{n})^{T},\quad p_{1},\dotsc ,{\text{ and }}p_{n}\geq 0,p_{1}+\dotsb +p_{n}=1} 有限离散分布 X ∼ FD ( x , p ) {\displaystyle X\sim \operatorname {FD} (\mathbf {x} ,\mathbf {p} )} f ( x i ; p ) = p i , i = 1 , … , or n . {\displaystyle f(x_{i};\mathbf {p} )=p_{i},\quad i=1,\dotsc ,{\text{ or }}n.}
备注。
对于均值和方差,我们可以直接根据定义进行计算。有限离散分布没有特殊的公式。
定义。 (离散均匀分布) 离散均匀分布 D U { x 1 , … , x n } {\displaystyle \operatorname {D} {\mathcal {U}}\{x_{1},\dotsc ,x_{n}\}} FD ( x , p ) , p = ( 1 n , … , 1 n ⏟ n times ) T {\displaystyle \operatorname {FD} (\mathbf {x} ,\mathbf {p} ),\quad \mathbf {p} ={\bigg (}\underbrace {{\frac {1}{n}},\dotsc ,{\frac {1}{n}}} _{n{\text{ times}}}{\bigg )}^{T}}
备注。
它的概率质量函数为 f ( x i ) = 1 n , i = 1 , … , or n . {\displaystyle f(x_{i})={\frac {1}{n}},\quad i=1,\dotsc ,{\text{ or }}n.}
示例。 假设随机变量 X ∼ FD ( ( 1 , 2 , 3 ) T , ( 0.2 , 0.3 , 0.5 ) T ) {\displaystyle X\sim \operatorname {FD} {\big (}(1,2,3)^{T},(0.2,0.3,0.5)^{T}{\big )}} P ( X = 1 ) = 0.2 , P ( X = 2 ) = 0.3 , and P ( X = 3 ) = 0.5. {\displaystyle \mathbb {P} (X=1)=0.2,\mathbb {P} (X=2)=0.3,{\text{ and }}\mathbb {P} (X=3)=0.5.}
|
| *
| |
| * |
| * | |
| | | |
*----*----*----*-------
1 2 3
示例。 假设随机变量 X ∼ D U { 1 , 2 , 3 } {\displaystyle X\sim \operatorname {D} {\mathcal {U}}\{1,2,3\}} P ( X = 1 ) = P ( X = 2 ) = P ( X = 3 ) = 1 3 . {\displaystyle \mathbb {P} (X=1)=\mathbb {P} (X=2)=\mathbb {P} (X=3)={\frac {1}{3}}.}
|
|
|
| * * *
| | | |
| | | |
*----*----*----*-------
1 2 3
练习。
连续均匀分布 相同的概率 [ 9] 离散 连续 连续
定义。 (均匀分布)
U [ a , b ] {\displaystyle {\color {dodgerblue}{\mathcal {U}}[a,b]}} 如果随机变量 X {\displaystyle X} 均匀分布 X ∼ U [ a , b ] {\displaystyle X\sim {\mathcal {U}}[a,b]} f ( x ) = 1 / ( b − a ) , x ∈ supp ( X ) = [ a , b ] , and a ≤ b . {\displaystyle f(x)=1/(b-a),\quad x\in \operatorname {supp} (X)=[a,b],{\text{ and }}a\leq b.}
备注。
U [ a , b ] {\displaystyle {\mathcal {U}}[a,b]} [ a , b ) , ( a , b ] {\displaystyle [a,b),(a,b]} ( a , b ) {\displaystyle (a,b)} 单一 零 U [ 0 , 1 ] {\displaystyle {\mathcal {U}}[0,1]} 标准均匀分布
命题。
U [ a , b ] {\displaystyle {\color {dodgerblue}{\mathcal {U}}[a,b]}} (均匀分布的 cdf) U [ a , b ] {\displaystyle {\mathcal {U}}[a,b]} F ( x ) = { 0 , x < a ; ( x − a ) / ( b − a ) , a ≤ x ≤ b ; 1 , x > b . {\displaystyle F(x)={\begin{cases}0,&x<a;\\(x-a)/(b-a),&a\leq x\leq b;\\1,&x>b.\end{cases}}}
证明。 F ( x ) = ∫ − ∞ x 1 { a ≤ x ≤ b } b − a d y = 1 b − a ∫ a x 1 { a ≤ x ≤ b } d y = { 0 / ( b − a ) , x < a ; [ y ] a x / ( b − a ) , a ≤ x ≤ b ; [ y ] a b / ( b − a ) , x > b . {\displaystyle F(x)=\int _{-\infty }^{x}{\frac {\mathbf {1} \{a\leq x\leq b\}}{b-a}}\,dy={\frac {1}{b-a}}\int _{a}^{x}\mathbf {1} \{a\leq x\leq b\}\,dy={\begin{cases}0/(b-a),&x<a;\\[][y]_{a}^{x}/(b-a),&a\leq x\leq b;\\[][y]_{a}^{b}/(b-a),&x>b.\end{cases}}}
◻ {\displaystyle \Box }
带有速率参数 λ {\displaystyle \lambda } 指数 λ {\displaystyle \lambda } 到达时间间隔
与 泊松 指数 泊松 数量
根据 速率 速率 ↑ {\displaystyle \uparrow } 到达时间间隔 ↓ {\displaystyle \downarrow } ↑ {\displaystyle \uparrow }
因此,我们希望当 λ ↑ {\displaystyle \lambda \uparrow } λ ↑ {\displaystyle \lambda \uparrow } x {\displaystyle x} λ ↑ {\displaystyle \lambda \uparrow } x {\displaystyle x} ↑ {\displaystyle \uparrow }
此外,由于速率 λ {\displaystyle \lambda } 递减 x ↑ {\displaystyle x\uparrow } ↓ {\displaystyle \downarrow }
如我们所见,指数分布的 pdf 满足这两个性质。
证明。 假设 X ∼ Exp ( λ ) {\displaystyle X\sim \operatorname {Exp} (\lambda )} X {\displaystyle X} F ( x ) = ∫ − ∞ x λ e − λ y 1 { y ≥ 0 } d y = { ∫ 0 x λ e − λ y d y , x ≥ 0 ; 0 , x < 0 ( When x < 0 , x ∉ supp ( X ) , so F ( x ) = P ( X ≤ x ) = 0 ) = 1 { x ≥ 0 } λ ∫ 0 x e − λ y d y = 1 { x ≥ 0 } λ − λ [ e − λ y ] 0 x = − 1 { x ≥ 0 } ( e − λ x − 1 ) = ( 1 − e − λ x ) 1 { x ≥ 0 } . {\displaystyle {\begin{aligned}F(x)&=\int _{-\infty }^{x}\lambda e^{-\lambda y}\mathbf {1} \{y\geq 0\}\,dy\\&={\begin{cases}\int _{0}^{x}\lambda e^{-\lambda y}\,dy,&x\geq 0;\\0,&x<0\\\end{cases}}&\left({\text{When }}x<0,x\notin \operatorname {supp} (X),{\text{ so }}F(x)=\mathbb {P} (X\leq x)=0\right)\\&=\mathbf {1} \{x\geq 0\}\lambda \int _{0}^{x}e^{-\lambda y}\,dy\\&=\mathbf {1} \{x\geq 0\}{\frac {\lambda }{-\lambda }}[e^{-\lambda }y]_{0}^{x}\\&=-\mathbf {1} \{x\geq 0\}(e^{-\lambda x}-1)\\&=(1-e^{-\lambda x})\mathbf {1} \{x\geq 0\}.\\\end{aligned}}}
◻ {\displaystyle \Box }
证明。 P ( X > s + t | X > s ) = def P ( X > s + t ∩ X > s ) P ( X > s ) = P ( X > s + t ) P ( X > s ) = 1 − ( 1 − e − λ ( s + t ) ) 1 − ( 1 − e − λ s ) = e − λ ( s + t ) e − λ s = e − λ t = P ( X > t ) . {\displaystyle \mathbb {P} (X>s+t|X>s){\overset {\text{ def }}{=}}{\frac {\mathbb {P} (X>s+t\cap X>s)}{\mathbb {P} (X>s)}}={\frac {\mathbb {P} (X>s+t)}{\mathbb {P} (X>s)}}={\frac {1-(1-e^{-\lambda (s+t)})}{1-(1-e^{-\lambda s})}}={\frac {e^{-\lambda (s+t)}}{e^{-\lambda s}}}=e^{-\lambda t}=\mathbb {P} (X>t).}
◻ {\displaystyle \Box }
Gamma 指数 形状 指数
定义。 (Gamma 分布)
Gamma ( 1 , 1 ) , Gamma ( 2 , 1 ) , Gamma ( 3 , 1 ) {\displaystyle {\color {red}\operatorname {Gamma} (1,1)},{\color {green}\operatorname {Gamma} (2,1)},{\color {blue}\operatorname {Gamma} (3,1)}} Gamma ( 3 , 0.5 ) {\displaystyle {\color {magenta}\operatorname {Gamma} (3,0.5)}} 随机变量 X {\displaystyle X} 伽马分布 形状 α {\displaystyle \alpha } 速率 λ {\displaystyle \lambda } X ∼ Gamma ( α , λ ) {\displaystyle X\sim \operatorname {Gamma} (\alpha ,\lambda )} f ( x ) = λ α x α − 1 e − λ x Γ ( α ) , x ∈ supp ( X ) = [ 0 , ∞ ) . {\displaystyle f(x)={\frac {\lambda ^{\alpha }x^{\alpha -1}e^{-\lambda x}}{\Gamma (\alpha )}},\quad x\in \operatorname {supp} (X)=[0,\infty ).}
Gamma ( 1 , 1 ) , Gamma ( 2 , 1 ) , Gamma ( 3 , 1 ) {\displaystyle {\color {red}\operatorname {Gamma} (1,1)},{\color {green}\operatorname {Gamma} (2,1)},{\color {blue}\operatorname {Gamma} (3,1)}} Gamma ( 3 , 0.5 ) {\displaystyle {\color {magenta}\operatorname {Gamma} (3,0.5)}}
贝塔 U [ 0 , 1 ] {\displaystyle {\mathcal {U}}[0,1]} 两个形状参数 形状
定义。 (贝塔分布)
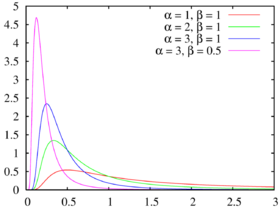
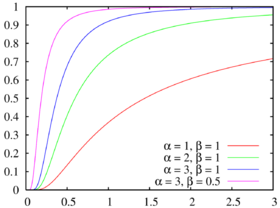
以下是 Beta ( 0.5 , 0.5 ) , Beta ( 5 , 1 ) , Beta ( 1 , 3 ) {\displaystyle {\color {red}\operatorname {Beta} (0.5,0.5)},{\color {royalblue}\operatorname {Beta} (5,1)},{\color {green}\operatorname {Beta} (1,3)}} Beta ( 2 , 2 ) {\displaystyle {\color {purple}\operatorname {Beta} (2,2)}} Beta ( 2 , 5 ) {\displaystyle {\color {darkorange}\operatorname {Beta} (2,5)}} 随机变量 X {\displaystyle X} beta 分布 α {\displaystyle \alpha } β {\displaystyle \beta } X ∼ Beta ( α , β ) {\displaystyle X\sim \operatorname {Beta} (\alpha ,\beta )} f ( x ) = Γ ( α + β ) Γ ( α ) Γ ( β ) x α − 1 ( 1 − x ) β − 1 , x ∈ supp ( X ) = [ 0 , 1 ] . {\displaystyle f(x)={\frac {\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}}x^{\alpha -1}(1-x)^{\beta -1},\quad x\in \operatorname {supp} (X)=[0,1].}
以下是 Beta ( 0.5 , 0.5 ) , Beta ( 5 , 1 ) , Beta ( 1 , 3 ) {\displaystyle {\color {red}\operatorname {Beta} (0.5,0.5)},{\color {royalblue}\operatorname {Beta} (5,1)},{\color {green}\operatorname {Beta} (1,3)}} Beta ( 2 , 2 ) {\displaystyle {\color {purple}\operatorname {Beta} (2,2)}} Beta ( 2 , 5 ) {\displaystyle {\color {darkorange}\operatorname {Beta} (2,5)}}
备注。
Beta ( 1 , 1 ) ≡ U [ 0 , 1 ] {\displaystyle \operatorname {Beta} (1,1)\equiv {\mathcal {U}}[0,1]} Beta ( 1 , 1 ) {\displaystyle \operatorname {Beta} (1,1)} f ( x ) = Γ ( 2 ) ⏞ = 1 ! = 1 Γ ( 1 ) ⏟ = 0 ! = 1 Γ ( 1 ) x 1 − 1 ( 1 − x ) 1 − 1 1 { 0 ≤ x ≤ 1 } = 1 { 0 ≤ x ≤ 1 } , {\displaystyle f(x)={\frac {\overbrace {\Gamma (2)} ^{=1!=1}}{\underbrace {\Gamma (1)} _{=0!=1}\Gamma (1)}}x^{1-1}(1-x)^{1-1}\mathbf {1} \{0\leq x\leq 1\}=\mathbf {1} \{0\leq x\leq 1\},}
这是 U [ 0 , 1 ] {\displaystyle {\mathcal {U}}[0,1]}
柯西分布是一种 重尾 [ 10] 似乎
备注。
此定义指的是柯西分布的一个 特例 尺度 Pdf 关于 θ {\displaystyle \theta } f ( θ + x ) = f ( θ − x ) {\displaystyle f(\theta +x)=f(\theta -x)}
正态分布或高斯分布是一个美丽的事物,它出现在自然界的许多地方。这可能是因为样本均值或样本和经常 近似 正态 中心极限定理 正态
定义。 (正态分布)
N ( 0 , 0.2 ) , N ( 0 , 1 ) , N ( 0 , 5 ) {\displaystyle {\color {blue}{\mathcal {N}}(0,0.2)},{\color {red}{\mathcal {N}}(0,1)},{\color {darkorange}{\mathcal {N}}(0,5)}} N ( − 2 , 0.5 ) {\displaystyle {\color {darkgreen}{\mathcal {N}}(-2,0.5)}} 随机变量 X {\displaystyle X} 正态分布 均值 μ {\displaystyle \mu } 方差 σ 2 {\displaystyle \sigma ^{2}} X ∼ N ( μ , σ 2 ) {\displaystyle X\sim {\mathcal {N}}(\mu ,\sigma ^{2})} f ( x ) = 1 2 π σ 2 exp ( − ( x − μ ) 2 2 σ 2 ) , x ∈ supp ( X ) = R . {\displaystyle f(x)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right),\quad x\in \operatorname {supp} (X)=\mathbb {R} .}
N ( 0 , 0.2 ) , N ( 0 , 1 ) , N ( 0 , 5 ) {\displaystyle {\color {blue}{\mathcal {N}}(0,0.2)},{\color {red}{\mathcal {N}}(0,1)},{\color {darkorange}{\mathcal {N}}(0,5)}} N ( − 2 , 0.5 ) {\displaystyle {\color {darkgreen}{\mathcal {N}}(-2,0.5)}}
以下分布在统计学中尤为重要,它们都与正态分布有关。我们将简要介绍它们。
卡方 标准正态
定义。 (卡方分布)
的 pdf χ 1 2 , χ 2 2 , χ 3 2 , χ 4 2 , χ 6 2 {\displaystyle {\color {darkorange}\chi _{1}^{2}},{\color {green}\chi _{2}^{2}},{\color {royalblue}\chi _{3}^{2}},{\color {blue}\chi _{4}^{2}},{\color {purple}\chi _{6}^{2}}} χ 9 2 {\displaystyle {\color {red}\chi _{9}^{2}}} 具有正的自由度的卡方分布 ν {\displaystyle {\color {blue}\nu }} χ ν 2 {\displaystyle \chi _{\color {blue}\nu }^{2}} Z 1 2 + ⋯ + Z ν 2 {\displaystyle Z_{1}^{2}+\dotsb +Z_{\color {blue}\nu }^{2}} Z 1 , … , Z ν {\displaystyle Z_{1},\dotsc ,Z_{\color {blue}\nu }} N ( 0 , 1 ) {\displaystyle {\mathcal {N}}(0,1)}
的 cdf χ 1 2 , χ 2 2 , χ 3 2 , χ 4 2 , χ 6 2 {\displaystyle {\color {darkorange}\chi _{1}^{2}},{\color {green}\chi _{2}^{2}},{\color {royalblue}\chi _{3}^{2}},{\color {blue}\chi _{4}^{2}},{\color {purple}\chi _{6}^{2}}} χ 9 2 {\displaystyle {\color {red}\chi _{9}^{2}}}
学生t分布 卡方 正态
定义. (学生 t {\displaystyle t}
t 1 , t 2 , t 5 {\displaystyle {\color {darkorange}t_{1}},{\color {purple}t_{2}},{\color {royalblue}t_{5}}} t ∞ {\displaystyle t_{\infty }} 带有 ν {\displaystyle {\color {blue}\nu }} 学生 t {\displaystyle t} t ν {\displaystyle t_{\color {blue}\nu }} Z Y / ν {\displaystyle {\frac {Z}{\sqrt {Y/{\color {blue}\nu }}}}} Y ∼ χ ν 2 {\displaystyle Y\sim \chi _{\color {blue}\nu }^{2}} Z ∼ N ( 0 , 1 ) {\displaystyle Z\sim {\mathcal {N}}(0,1)}
t 1 , t 2 , t 5 {\displaystyle {\color {darkorange}t_{1}},{\color {purple}t_{2}},{\color {royalblue}t_{5}}} t ∞ {\displaystyle t_{\infty }}
F {\displaystyle F} t {\displaystyle t}
定义。 ( F {\displaystyle F} ν 1 {\displaystyle {\color {red}\nu _{1}}} ν 2 {\displaystyle {\color {blue}\nu _{2}}} F {\displaystyle F} F ν 1 , ν 2 {\displaystyle F_{{\color {red}\nu _{1}},{\color {blue}\nu _{2}}}} X 1 / ν 1 X 2 / ν 2 {\displaystyle {\frac {X_{1}/{\color {red}\nu _{1}}}{X_{2}/{\color {blue}\nu _{2}}}}} X 1 ∼ χ ν 1 2 {\displaystyle X_{1}\sim \chi _{\color {red}\nu _{1}}^{2}} X 2 ∼ χ ν 2 2 {\displaystyle X_{2}\sim \chi _{\color {blue}\nu _{2}}^{2}}
F 1 , 1 , F 2 , 1 , F 5 , 2 , F 10 , 1 {\displaystyle {\color {red}F_{1,1}},F_{2,1},{\color {blue}F_{5,2}},{\color {green}F_{10,1}}} F 100 , 100 {\displaystyle {\color {dimgray}F_{100,100}}} F 1 , 1 , F 2 , 1 , F 5 , 2 , F 10 , 1 {\displaystyle {\color {red}F_{1,1}},F_{2,1},{\color {blue}F_{5,2}},{\color {green}F_{10,1}}} F 100 , 100 {\displaystyle {\color {dimgray}F_{100,100}}}
如果您想了解卡方分布 学生 t {\displaystyle t} F {\displaystyle F} 统计学/区间估计 (置信区间构建中的应用)和 统计学/假设检验 (假设检验中的应用)。
多项式分布是广义
假设有 n {\displaystyle n} k {\displaystyle k} 一个且仅一个 i {\displaystyle i} p i {\displaystyle p_{i}} i = 1 , 2 , … , k {\displaystyle i=1,2,\dotsc ,k} [ 12] X i {\displaystyle X_{i}} i {\displaystyle i} P ( X = def ( X 1 , … , X k ) T = x = def ( x 1 , … , x k ) T ) {\displaystyle \mathbb {P} {\big (}\mathbf {X} {\overset {\text{ def }}{=}}(X_{1},\dotsc ,X_{k})^{T}=\mathbf {x} {\overset {\text{ def }}{=}}(x_{1},\dotsc ,x_{k})^{T}{\big )}} i {\displaystyle i} x i {\displaystyle x_{i}}
我们可以将每个分配视为一个独立的试验,有 k {\displaystyle k} k {\displaystyle k} n {\displaystyle n} n {\displaystyle n} k {\displaystyle k} ( n x 1 , … , x k ) {\displaystyle {\binom {n}{x_{1},\dotsc ,x_{k}}}}
所以, P ( X = x ) = ( n x 1 , … , x k ) p 1 x 1 ⋯ p k x k . {\displaystyle \mathbb {P} (\mathbf {X} =\mathbf {x} )={\binom {n}{x_{1},\dotsc ,x_{k}}}p_{1}^{x_{1}}\dotsb p_{k}^{x_{k}}.} x i {\displaystyle x_{i}} i {\displaystyle i} p i x i {\displaystyle p_{i}^{x_{i}}} n {\displaystyle n} k {\displaystyle k} p 1 x 1 ⋯ p k x k {\displaystyle p_{1}^{x_{1}}\dotsb p_{k}^{x_{k}}}
定义. (多项式分布) 一个随机向量 X = ( X 1 , … , X k ) T {\displaystyle \mathbf {X} =(X_{1},\dotsc ,X_{k})^{T}} 多项式分布 n {\displaystyle n} p = ( p 1 , … , p k ) T {\displaystyle \mathbf {p} =(p_{1},\dotsc ,p_{k})^{T}} X ∼ Multinom ( n , p ) {\displaystyle \mathbf {X} \sim \operatorname {Multinom} (n,\mathbf {p} )} f X ( x 1 , … , x k ; n , p ) = ( n x 1 , … , x k ) p 1 x 1 ⋯ p k x k , x 1 , … , x k ≥ 0 , and x 1 + ⋯ + x k = n . {\displaystyle f_{\mathbf {X} }(x_{1},\dotsc ,x_{k};n,\mathbf {p} )={\binom {n}{x_{1},\dotsc ,x_{k}}}p_{1}^{x_{1}}\dotsb p_{k}^{x_{k}},\quad x_{1},\dotsc ,x_{k}\geq 0,{\text{ and }}x_{1}+\dotsb +x_{k}=n.}
备注。
Multinom ( n , p ) ≡ Binom ( n , p ) {\displaystyle \operatorname {Multinom} (n,\mathbf {p} )\equiv \operatorname {Binom} (n,p)} p = ( p , 1 − p ) T {\displaystyle \mathbf {p} =(p,1-p)^{T}} 在这种情况下,如果 ( X 1 , X 2 ) T ∼ Multinom ( n , p ) {\displaystyle (X_{1},X_{2})^{T}\sim \operatorname {Multinom} (n,\mathbf {p} )} X 1 {\displaystyle X_{1}} X 2 ( = n − X 1 ) {\displaystyle X_{2}(=n-X_{1})} 此外, X i ∼ Binom ( n , p i ) {\displaystyle X_{i}\sim \operatorname {Binom} (n,p_{i})} i {\displaystyle i} [ 13] p i {\displaystyle p_{i}}
多元
Definition. (Multivariate normal distribution) A random vector X = ( X 1 , … , X k ) T {\displaystyle \mathbf {X} =(X_{1},\dotsc ,X_{k})^{T}} k {\displaystyle k} mean vector μ {\displaystyle {\boldsymbol {\mu }}} covariance matrix Σ {\displaystyle {\boldsymbol {\Sigma }}} X ∼ N k ( μ , Σ ) {\displaystyle \mathbf {X} \sim {\mathcal {N}}_{k}({\boldsymbol {\mu }},{\boldsymbol {\Sigma }})} [ 14] f X ( x 1 , … , x k ; μ , Σ ) = exp ( − ( x − μ ) T Σ − 1 ( x − μ ) / 2 ) ( 2 π ) k det Σ , x = ( x 1 , … , x k ) T ∈ R k {\displaystyle f_{\mathbf {X} }(x_{1},\dotsc ,x_{k};{\boldsymbol {\mu }},{\boldsymbol {\Sigma }})={\frac {\exp \left(-(\mathbf {x} -{\boldsymbol {\mu }})^{T}{\boldsymbol {\Sigma }}^{-1}(\mathbf {x} -{\boldsymbol {\mu }})/2\right)}{\sqrt {(2\pi )^{k}\det {\boldsymbol {\Sigma }}}}},\quad \mathbf {x} =(x_{1},\dotsc ,x_{k})^{T}\in \mathbb {R} ^{k}} μ = ( μ 1 , … , μ k ) T = ( E [ X 1 ] , … , E [ X k ] ) T {\displaystyle {\boldsymbol {\mu }}=(\mu _{1},\dotsc ,\mu _{k})^{T}=(\mathbb {E} [X_{1}],\dotsc ,\mathbb {E} [X_{k}])^{T}} mean vector Σ = ( Cov ( X 1 , X 1 ) ⋯ Cov ( X 1 , X k ) ⋮ ⋱ ⋮ Cov ( X k , X 1 ) ⋯ Cov ( X k , X k ) ) = ( σ 1 2 ⋯ Cov ( X 1 , X k ) ⋮ ⋱ ⋮ Cov ( X k , X 1 ) ⋯ σ k 2 ) {\displaystyle {\boldsymbol {\Sigma }}={\begin{pmatrix}\operatorname {Cov} (X_{1},X_{1})&\cdots &\operatorname {Cov} (X_{1},X_{k})\\\vdots &\ddots &\vdots \\\operatorname {Cov} (X_{k},X_{1})&\cdots &\operatorname {Cov} (X_{k},X_{k})\end{pmatrix}}={\begin{pmatrix}\sigma _{1}^{2}&\cdots &\operatorname {Cov} (X_{1},X_{k})\\\vdots &\ddots &\vdots \\\operatorname {Cov} (X_{k},X_{1})&\cdots &\sigma _{k}^{2}\end{pmatrix}}} covariance matrix k × k {\displaystyle k\times k}
备注。
情况 k = 2 {\displaystyle k=2} 双变量正态
一个替代且等效的定义是 X = ( X 1 , … , X k ) T ∼ N k ( μ , Σ ) {\displaystyle \mathbf {X} =(X_{1},\dotsc ,X_{k})^{T}\sim {\mathcal {N}}_{k}({\boldsymbol {\mu }},{\boldsymbol {\Sigma }})} X 1 = a 11 Z 1 + ⋯ + a 1 n Z n + μ 1 ; ⋮ X k = a k 1 Z 1 + ⋯ + a k n Z n + μ k , {\displaystyle {\begin{aligned}X_{1}&=a_{11}Z_{1}+\dotsb +a_{1n}Z_{n}+\mu _{1};\\\vdots \\X_{k}&=a_{k1}Z_{1}+\dotsb +a_{kn}Z_{n}+\mu _{k},\\\end{aligned}}}
对于一些常数 a 11 , … , a 1 n , … , a k 1 , … , a k n , μ 1 , … , μ k {\displaystyle a_{11},\dotsc ,a_{1n},\dotsc ,a_{k1},\dotsc ,a_{kn},\mu _{1},\dotsc ,\mu _{k}} Z 1 , … , Z n {\displaystyle Z_{1},\dotsc ,Z_{n}} n {\displaystyle n} 利用上述结果, X i {\displaystyle X_{i}} 边缘 N ( μ i , σ i 2 ) , i = 1 , 2 , … , or k {\displaystyle {\mathcal {N}}(\mu _{i},\sigma _{i}^{2}),\quad i=1,2,\dotsc ,{\text{ or }}k} 根据独立正态随机变量之和的命题以及正态随机变量线性变换的分布(参见概率/随机变量的变换 章节),均值为 0 + ⋯ + 0 + μ i = μ i {\displaystyle 0+\dotsb +0+\mu _{i}=\mu _{i}} a i 1 2 + ⋯ + a i n 2 {\displaystyle a_{i1}^{2}+\dotsb +a_{in}^{2}} σ i 2 {\displaystyle \sigma _{i}^{2}}
命题。 (双变量正态分布的联合概率密度函数) N 2 ( μ , Σ ) {\displaystyle {\mathcal {N}}_{2}({\boldsymbol {\mu }},{\boldsymbol {\Sigma }})} f ( x , y ) = 1 2 π σ X σ Y 1 − ρ 2 exp ( − 1 2 ( 1 − ρ 2 ) ( ( x − μ X σ X ) 2 − 2 ρ ( x − μ X σ X ) ( y − μ Y σ Y ) + ( y − μ Y σ Y ) 2 ) ) , ( x , y ) T ∈ R 2 {\displaystyle f(x,y)={\frac {1}{2\pi \sigma _{X}\sigma _{Y}{\sqrt {1-\rho ^{2}}}}}\exp \left(-{\frac {1}{2(1-\rho ^{2})}}\left(\left({\frac {x-\mu _{X}}{\sigma _{X}}}\right)^{2}-2\rho \left({\frac {x-\mu _{X}}{\sigma _{X}}}\right)\left({\frac {y-\mu _{Y}}{\sigma _{Y}}}\right)+\left({\frac {y-\mu _{Y}}{\sigma _{Y}}}\right)^{2}\right)\right),\quad (x,y)^{T}\in \mathbb {R} ^{2}}
其中
ρ = ρ ( X , Y ) {\displaystyle \rho =\rho (X,Y)} 且
σ X , σ Y {\displaystyle \sigma _{X},\sigma _{Y}} 为正数。
双变量正态分布示例图
证明。 对于双变量正态分布,
均值向量 μ = ( μ X , μ Y ) {\displaystyle {\boldsymbol {\mu }}=(\mu _{X},\mu _{Y})} 该 协方差矩阵 Σ = ( Cov ( X , X ) Cov ( X , Y ) Cov ( Y , X ) Cov ( Y , Y ) ) = ( Var ( X ) Cov ( X , Y ) Cov ( X , Y ) Var ( Y ) ) = ( σ X 2 ρ σ X σ Y ρ σ X σ Y σ Y 2 ) . {\displaystyle {\boldsymbol {\Sigma }}={\begin{pmatrix}\operatorname {Cov} (X,X)&\operatorname {Cov} (X,Y)\\\operatorname {Cov} (Y,X)&\operatorname {Cov} (Y,Y)\end{pmatrix}}={\begin{pmatrix}\operatorname {Var} (X)&\operatorname {Cov} (X,Y)\\\operatorname {Cov} (X,Y)&\operatorname {Var} (Y)\\\end{pmatrix}}={\begin{pmatrix}\sigma _{X}^{2}&\rho \sigma _{X}\sigma _{Y}\\\rho \sigma _{X}\sigma _{Y}&\sigma _{Y}^{2}\\\end{pmatrix}}.}
因此, ( x − μ ) T Σ − 1 ( x − μ ) = 1 det Σ ( ( x − μ X , y − μ Y ) T ) T ( σ Y 2 − ρ σ X σ Y − ρ σ X σ Y σ X 2 ) ( x − μ X , y − μ Y ) T ) = 1 det Σ ( x − μ X y − μ Y ) ( σ Y 2 − ρ σ X σ Y − ρ σ X σ Y σ X 2 ) ( x − μ X y − μ Y ) = 1 det Σ ( ( x − μ X ) σ Y 2 − ( y − μ Y ) ρ σ X σ Y − ( x − μ X ) ρ σ X σ Y + ( y − μ Y ) σ X 2 ) ( x − μ X y − μ Y ) = 1 det Σ ⏟ σ X 2 σ Y 2 − ( ρ σ X σ Y ) 2 ( ( x − μ X ) 2 σ Y 2 − ( x − μ X ) ( y − μ Y ) ρ σ X σ Y − ( x − μ X ) ( y − μ Y ) ρ σ X σ Y ⏟ = − 2 ρ ( x − μ X ) ( y − μ Y ) σ X σ Y + ( y − μ Y ) 2 σ X 2 ) = ( x − μ X ) 2 σ Y 2 − 2 ρ ( x − μ X ) ( y − μ Y ) σ X σ Y + ( y − μ Y ) 2 σ X 2 σ X 2 σ Y 2 ( 1 − ρ ) 2 = 1 1 − ρ 2 ( ( x − μ X σ X ) 2 − 2 ρ ( ( x − μ X ) ( y − μ Y ) σ X σ Y ) + ( y − μ Y σ Y ) 2 ) . {\displaystyle {\begin{aligned}(\mathbf {x} -{\boldsymbol {\mu }})^{T}{\boldsymbol {\Sigma }}^{-1}(\mathbf {x} -{\boldsymbol {\mu }})&={\frac {1}{\det {\boldsymbol {\Sigma }}}}\left((x-\mu _{X},y-\mu _{Y})^{T}\right)^{T}{\begin{pmatrix}\sigma _{Y}^{2}&-\rho \sigma _{X}\sigma _{Y}\\-\rho \sigma _{X}\sigma _{Y}&\sigma _{X}^{2}\\\end{pmatrix}}(x-\mu _{X},y-\mu _{Y})^{T})\\&={\frac {1}{\det {\boldsymbol {\Sigma }}}}{\begin{pmatrix}{\color {blue}x-\mu _{X}}&{\color {red}y-\mu _{Y}}\end{pmatrix}}{\begin{pmatrix}{\color {darkgreen}\sigma _{Y}^{2}}&{\color {darkorange}-\rho \sigma _{X}\sigma _{Y}}\\{\color {purple}-\rho \sigma _{X}\sigma _{Y}}&{\color {maroon}\sigma _{X}^{2}}\\\end{pmatrix}}{\begin{pmatrix}x-\mu _{X}\\y-\mu _{Y}\end{pmatrix}}\\&={\frac {1}{\det {\boldsymbol {\Sigma }}}}{\begin{pmatrix}{\color {blue}(x-\mu _{X})}{\color {darkgreen}\sigma _{Y}^{2}}{\color {purple}-}{\color {red}(y-\mu _{Y})}{\color {purple}\rho \sigma _{X}\sigma _{Y}}&{\color {darkorange}-}{\color {blue}(x-\mu _{X})}{\color {darkorange}\rho \sigma _{X}\sigma _{Y}}+{\color {red}(y-\mu _{Y})}{\color {maroon}\sigma _{X}^{2}}\end{pmatrix}}{\begin{pmatrix}{\color {deeppink}x-\mu _{X}}\\{\color {deeppink}y-\mu _{Y}}\end{pmatrix}}\\&={\frac {1}{\underbrace {\det {\boldsymbol {\Sigma }}} _{\sigma _{X}^{2}\sigma _{Y}^{2}-(\rho \sigma _{X}\sigma _{Y})^{2}}}}{\big (}(x-\mu _{X})^{\color {deeppink}2}\sigma _{Y}^{2}\underbrace {-{\color {deeppink}(x-\mu _{X})}(y-\mu _{Y})\rho \sigma _{X}\sigma _{Y}-(x-\mu _{X}){\color {deeppink}(y-\mu _{Y})}\rho \sigma _{X}\sigma _{Y}} _{=-2\rho (x-\mu _{X})(y-\mu _{Y})\sigma _{X}\sigma _{Y}}+(y-\mu _{Y})^{\color {deeppink}2}\sigma _{X}^{2}{\big )}\\&={\frac {(x-\mu _{X})^{2}\sigma _{Y}^{2}-2\rho (x-\mu _{X})(y-\mu _{Y})\sigma _{X}\sigma _{Y}+(y-\mu _{Y})^{2}\sigma _{X}^{2}}{\sigma _{X}^{2}\sigma _{Y}^{2}(1-\rho )^{2}}}\\&={\frac {1}{1-\rho ^{2}}}\left(\left({\frac {x-\mu _{X}}{\sigma _{X}}}\right)^{2}-2\rho \left({\frac {(x-\mu _{X})(y-\mu _{Y})}{\sigma _{X}\sigma _{Y}}}\right)+\left({\frac {y-\mu _{Y}}{\sigma _{Y}}}\right)^{2}\right).\end{aligned}}}
f ( x , y ) = 1 ( 2 π ) 2 det Σ exp ( − 1 2 ⋅ 1 1 − ρ 2 ( ( x − μ X σ X ) 2 − 2 ρ ( ( x − μ X ) ( y − μ Y ) σ X σ Y ) + ( y − μ Y σ Y ) 2 ) ) = 1 2 π σ X 2 σ Y 2 ( 1 − ρ 2 ) exp ( − 1 2 ( 1 − ρ 2 ) ( ( x − μ X σ X ) 2 − 2 ρ ( ( x − μ X ) ( y − μ Y ) σ X σ Y ) + ( y − μ Y σ Y ) 2 ) ) = 1 2 π σ X σ Y 1 − ρ 2 exp ( − 1 2 ( 1 − ρ 2 ) ( ( x − μ X σ X ) 2 − 2 ρ ( x − μ X σ X ) ( y − μ Y σ Y ) + ( y − μ Y σ Y ) 2 ) ) . {\displaystyle {\begin{aligned}f(x,y)&={\frac {1}{\sqrt {(2\pi )^{2}\det {\boldsymbol {\Sigma }}}}}\exp \left(-{\frac {1}{2}}\cdot {\frac {1}{1-\rho ^{2}}}\left(\left({\frac {x-\mu _{X}}{\sigma _{X}}}\right)^{2}-2\rho \left({\frac {(x-\mu _{X})(y-\mu _{Y})}{\sigma _{X}\sigma _{Y}}}\right)+\left({\frac {y-\mu _{Y}}{\sigma _{Y}}}\right)^{2}\right)\right)\\&={\frac {1}{2\pi {\sqrt {\sigma _{X}^{2}\sigma _{Y}^{2}(1-\rho ^{2})}}}}\exp \left({\frac {-1}{2(1-\rho ^{2})}}\left(\left({\frac {x-\mu _{X}}{\sigma _{X}}}\right)^{2}-2\rho \left({\frac {(x-\mu _{X})(y-\mu _{Y})}{\sigma _{X}\sigma _{Y}}}\right)+\left({\frac {y-\mu _{Y}}{\sigma _{Y}}}\right)^{2}\right)\right)\\&={\frac {1}{2\pi \sigma _{X}\sigma _{Y}{\sqrt {1-\rho ^{2}}}}}\exp \left({\frac {-1}{2(1-\rho ^{2})}}\left(\left({\frac {x-\mu _{X}}{\sigma _{X}}}\right)^{2}-2\rho \left({\frac {x-\mu _{X}}{\sigma _{X}}}\right)\left({\frac {y-\mu _{Y}}{\sigma _{Y}}}\right)+\left({\frac {y-\mu _{Y}}{\sigma _{Y}}}\right)^{2}\right)\right).\\\end{aligned}}}
◻ {\displaystyle \Box }
↑ 或者,我们可以将事件定义为 { i th Bernoulli trial is a failure } . {\displaystyle \{i{\text{th Bernoulli trial is a failure}}\}.} ↑ 'indpt.' 代表独立。 ↑ 这是因为存在对(可区分和有序)的无序选择 r {\displaystyle {\color {darkgreen}r}} '成功' ,从 n {\displaystyle {\color {blue}n}} '失败' )。 ↑ 将罕见事件的发生视为'成功',而罕见事件的未发生则视为'失败'。 ↑ 与二项分布的结果不同,每个 x {\displaystyle {\color {red}x}} 可能的 ↑ 从 x + k − 1 {\displaystyle {\color {red}x}+{\color {darkgreen}k}-1} x {\displaystyle {\color {red}x}} '失败' (或 k − 1 {\displaystyle {\color {darkgreen}k}-1} '成功' )的无序选择。 ↑ 对 k {\displaystyle k} x {\displaystyle x} ↑ 这超出了本书的范围。 ↑ 概率 '在区间上均匀分布'。 ↑ 与其他 轻尾 柯西 极端值 ↑ 对于 a < 0 {\displaystyle a<0} a = 0 {\displaystyle a=0} ↑ 那么, p 1 + p 2 + ⋯ + p k = 1 {\displaystyle p_{1}+p_{2}+\dotsb +p_{k}=1} ↑ 如果该对象被分配到除 i {\displaystyle i} ↑ 对于 N {\displaystyle {\mathcal {N}}} k {\displaystyle k} k {\displaystyle k} 






















































































































![{\displaystyle {\color {dodgerblue}{\mathcal {U}}[a,b]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e43064f6f5b6b3782a88f679aff01f560a756a5)
![{\displaystyle X\sim {\mathcal {U}}[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ef8f0bf7ccaa764ee9bf60944dec51559aa8a09)
![{\displaystyle f(x)=1/(b-a),\quad x\in \operatorname {supp} (X)=[a,b],{\text{ and }}a\leq b.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b9538bcba07e181297d1ea8bed39125abf37e33)
![{\displaystyle {\mathcal {U}}[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/140992400aff9597adf2989ac9a7c4540902ebe5)
![{\displaystyle [a,b),(a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c831c660bc5d57d59b3c2fb8e01b633bf726ba32)

![{\displaystyle {\mathcal {U}}[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1aec3afe927b9042f55a8c5ea4cbd1d9d97de55)


![{\displaystyle F(x)=\int _{-\infty }^{x}{\frac {\mathbf {1} \{a\leq x\leq b\}}{b-a}}\,dy={\frac {1}{b-a}}\int _{a}^{x}\mathbf {1} \{a\leq x\leq b\}\,dy={\begin{cases}0/(b-a),&x<a;\\[][y]_{a}^{x}/(b-a),&a\leq x\leq b;\\[][y]_{a}^{b}/(b-a),&x>b.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f1c057e9f6b1f0ddf5f74f1a8dcde00a4b52790)













![{\displaystyle {\begin{aligned}F(x)&=\int _{-\infty }^{x}\lambda e^{-\lambda y}\mathbf {1} \{y\geq 0\}\,dy\\&={\begin{cases}\int _{0}^{x}\lambda e^{-\lambda y}\,dy,&x\geq 0;\\0,&x<0\\\end{cases}}&\left({\text{When }}x<0,x\notin \operatorname {supp} (X),{\text{ so }}F(x)=\mathbb {P} (X\leq x)=0\right)\\&=\mathbf {1} \{x\geq 0\}\lambda \int _{0}^{x}e^{-\lambda y}\,dy\\&=\mathbf {1} \{x\geq 0\}{\frac {\lambda }{-\lambda }}[e^{-\lambda }y]_{0}^{x}\\&=-\mathbf {1} \{x\geq 0\}(e^{-\lambda x}-1)\\&=(1-e^{-\lambda x})\mathbf {1} \{x\geq 0\}.\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81bc9a6589d70ff54a7647210bf48053e9e59e92)




















![{\displaystyle f(x)={\frac {\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}}x^{\alpha -1}(1-x)^{\beta -1},\quad x\in \operatorname {supp} (X)=[0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7299f58655ef8cd2a8476dcda38fd376229ceba2)

![{\displaystyle \operatorname {Beta} (1,1)\equiv {\mathcal {U}}[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed813cf144d2362a448c73758ddbdda1dfe15fd1)








































![{\displaystyle {\begin{aligned}&&\phi (-y)&=\phi (y)\\&\Leftrightarrow &\int _{-\infty }^{x}\phi (-y)\,dy&=\int _{-\infty }^{x}\phi (y)\,dy\\&\Leftrightarrow &-\int _{\infty }^{-x}\phi (u)\,du&=\Phi (x)&{\text{let }}u=-y\Rightarrow dy=-dy.\\&\Leftrightarrow &[\Phi (u)]_{-x}^{\infty }&=\Phi (x)\\&\Leftrightarrow &\underbrace {\Phi (\infty )} _{=\mathbb {P} (\Omega )=1}-\Phi (-x)&=\Phi (x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cbcad71d39070a50f0c1c54a6378e488452564d)


































































![{\displaystyle {\boldsymbol {\mu }}=(\mu _{1},\dotsc ,\mu _{k})^{T}=(\mathbb {E} [X_{1}],\dotsc ,\mathbb {E} [X_{k}])^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f6f4faa98c1603023d57740ff2ae0fb06ba5406)

























