概率/随机变量

随机变量

动机

在许多实验中，样本空间中可能存在太多可能的结果，因此我们可能希望改为使用这些结果的“汇总变量”。例如，假设对 100 个人进行民意调查，询问他们是否同意某项提案。然后，为了完全跟踪这 100 个人的答案，我们可以先用数字表示他们的回答。

• 数字“1”表示“同意”。
• 数字“0”表示“不同意”。

(为了简单起见，我们假设只有这两个答案可用。)然后，为了记录每个人对哪个答案的回答，我们使用一个包含 100 个数字的向量进行记录。例如，$(1,0,1,0,0,\dotsc ,1,0,0)$，等等。由于向量中的每个坐标都有两个选择：“0”或“1”，因此样本空间中总共有 $2^{100}\approx 1.268\times 10^{30}$ 个不同的向量（用 $\Omega$ 表示）！因此，处理样本空间中如此多的结果非常繁琐和复杂 $\Omega$。相反，我们通常只关心有多少人“同意”和“不同意”，而不是每个人对哪个答案的回答，因为“同意”和“不同意”的数量决定了提案是否得到了他们中大多数人的同意，因此抓住了民意调查的本质。

因此，定义一个变量 $X$ 更方便，它给出样本空间中每个结果的 100 个坐标中的“1”的数量 $\Omega$。然后，$X$ 只能取 101 个可能的值：0, 1, 2, ..., 100，这远少于原始样本空间中的结果数。

通过这样做，我们可以将原始实验更改为一个新实验，其中变量 $X$ 根据一定的概率取 101 个可能的值中的一个。对于这个新实验，样本空间变为 $\{0,1,\dotsc ,100\}$。

在定义变量 $X$（称为 随机变量）的过程中，我们实际上（隐式地）定义了一个函数，其定义域是原始样本空间，值域是 $\{0,1,\dotsc ,100\}$。通常，我们将随机变量的陪域取为所有实数的集合 $\mathbb {R}$。也就是说，我们定义了随机变量 $X:\Omega \to \mathbb {R}$，其中 $$X(\omega )={\text{number of 1s in the coordinates of }}\omega$$ 对于每一个 $\omega \in \Omega$ 都成立。

定义

为了正式定义随机变量，我们需要可测函数的概念。

定义。（可测函数）令 $(A,\Sigma _{1})$ 和 $(B,\Sigma _{2})$ 是可测空间（也就是说，$\Sigma _{1}$ 和 $\Sigma _{2}$ 分别是 $\sigma$-代数 $A$ 和 $B$）。一个函数 $f:A\to B$ 是 ($\Sigma _{1}$-)可测，如果对于每一个 $Y\in \Sigma _{2}$，$f$ 下 $Y$ 的逆像 $$f^{-1}(Y)=\{x\in A:f(x)\in Y\}\in \Sigma _{1}.$$

备注。

• 如果 $f:A\to B$ 是 $\Sigma _{1}$-可测的，那么我们也可以写成 $f:(A,\Sigma _{1})\to (B,\Sigma _{2})$ 来强调对 $\sigma$-代数 $\Sigma _{1}$ 和 $\Sigma _{2}$ 的依赖。
• 我们只考虑集合 $Y$ 在 $\sigma$-代数 $\Sigma _{2}$ 中的原像，因为只有 $\Sigma _{2}$ 中的集合是“良好行为”的，因此它们是“感兴趣的”。然后，$f$ 的可测性确保原像也是“良好行为”的。

• 因此，可测函数在某种程度上保留了集合的“良好行为”。
• 事实证明，在定义中使用原像（而不是像）更有用。

定义。 (随机变量)

随机变量的图形说明。

令 $(\Omega ,{\mathcal {F}},\mathbb {P} )$ 是一个概率空间。一个 随机变量 是一个 ${\mathcal {F}}$-可测函数 $X:(\Omega ,{\mathcal {F}})\to (\mathbb {R} ,{\mathcal {B}})$.

备注。

• 通常，用大写字母来表示随机变量，用对应的小写字母来表示随机变量的实现值（即，从样本点映射的数值）。例如，我们说随机变量 $X$ 的实现值为 $x$.
• $\sigma$-代数 ${\mathcal {B}}$ 是 $\mathbb {R}$ 上的 Borel $\sigma$-代数。我们在这里将不会详细讨论它的定义。
• 由于 $X$ 是 ${\mathcal {F}}$-可测的，对于每个集合 $B\in {\mathcal {B}}$，原像 $X^{-1}(B)=\{\omega :X(\omega )\in B\}\in {\mathcal {F}}$。

• 通常用 $\{X\in B\}$ 来表示 $X^{-1}(B)$。此外，我们用 $\{X\leq x\},\{X=x\}$ 等来表示 $X^{-1}((-\infty ,x]),X^{-1}(\{x\})$ 等。

• 我们要求随机变量是 ${\mathcal {F}}$-可测的，以便概率 $\mathbb {P} (\{X\in B\})$（通常写成 $\mathbb {P} (X\in B)$）对于每个 $B\in {\mathcal {B}}$ 是 定义的。（概率测度的定义域是 ${\mathcal {F}}$，并且 $\{X\in B\}\in {\mathcal {F}}$ 是因为随机变量 $X$ 的 ${\mathcal {F}}$-可测性。）
• 一般而言，大多数我们能想到的函数（应该为随机变量）都是 ${\mathcal {F}}$-可测的。因此，我们假设这里构建的随机变量是 ${\mathcal {F}}$-可测的，因此实际上是有效的，无需证明。

通过定义一个从概率空间 $(\Omega ,{\mathcal {F}},\mathbb {P} )$ 到实数空间的随机变量 $X:\Omega \to \mathbb {R}$，我们实际上 诱导 出一个新的概率空间 $({\mathcal {X}},{\mathcal {F}}_{X},\mathbb {P} _{X})$，其中

• 诱导的样本空间 ${\mathcal {X}}$ 是随机变量 $X$ 的 值域：${\mathcal {X}}=\{X(\omega ):\omega \in \Omega \}\subseteq \mathbb {R}$。
• 诱导的事件空间 ${\mathcal {F}}_{X}$ 是 $\sigma$-代数 ${\mathcal {X}}$。（这里我们遵循之前的惯例：当 ${\mathcal {X}}$ 可数时，${\mathcal {F}}_{X}={\mathcal {P}}({\mathcal {X}})$。）
• 诱导的概率测度 $\mathbb {P} _{X}:{\mathcal {F}}_{X}\to [0,1]$ 定义为

$$\mathbb {P} _{X}(E)=\mathbb {P} (\{X\in E\})$$

对于每个 $E\in {\mathcal {F}}_{X}$。

结果证明，诱导的概率测度满足所有概率公理

例： 证明诱导概率测度 $\mathbb {P} _{X}$ 满足所有概率公理，因此是有效的。

证明： 非负性： 对于任何事件 $E\in {\mathcal {F}}_{X}$，$$\mathbb {P} _{X}(E)=\underbrace {\mathbb {P} (\{X\in E\})\geq 0} _{{\text{nonnegativity of }}\mathbb {P} }.$$ 单位性： 我们有 $$\mathbb {P} _{X}({\mathcal {X}})=\mathbb {P} (\{\omega \in \Omega :\underbrace {X(\omega )\in {\mathcal {X}}} _{\text{always true}}\})=\underbrace {\mathbb {P} (\Omega )=1} _{{\text{unitarity of }}\mathbb {P} }.$$ 特别地，对于任何 $\omega \in \Omega$，我们始终有 $X(\omega )\in {\mathcal {X}}$（因为 ${\mathcal {X}}$ 是随机变量 $X$ 的取值范围）。

可数可加性：对于任意一个两两不相交事件的无限序列 $E_{1},E_{2},\dotsc$（每个事件都属于 ${\mathcal {F}}_{X}$），$${\begin{aligned}\mathbb {P} \left(\bigcup _{i=1}^{\infty }E_{i}\right)&=\mathbb {P} \left(\left\{\omega \in \Omega :X(\omega )\in \bigcup _{i=1}^{\infty }E_{i}\right\}\right)\\&=\mathbb {P} \left(\bigcup _{i=1}^{\infty }\left\{\omega \in \Omega :X(\omega )\in E_{i}\right\}\right)\\&=\mathbb {P} \left({\color {blue}\bigcup _{i=1}^{\infty }}\bigcup _{x_{j}\in E_{i}}\left\{\omega \in \Omega :X(\omega )=x_{j}\right\}\right)\\&={\color {blue}\sum _{i=1}^{\infty }}\mathbb {P} \left(\bigcup _{x_{j}\in E_{i}}\left\{\omega \in \Omega :X(\omega )=x_{j}\right\}\right)&({\text{countable additivity of }}\mathbb {P} )\\&=\sum _{i=1}^{\infty }\mathbb {P} \left(\left\{\omega \in \Omega :X(\omega )\in E_{i}\right\}\right)\\&=\sum _{i=1}^{\infty }\mathbb {P} _{X}(E_{i}).\\\end{aligned}}$$

$\Box$

证明了这个结果后，可以得出之前讨论的所有概率测度的性质也适用于诱导的概率测度 $\mathbb {P} _{X}$。因此，我们可以利用概率测度的性质来计算概率 $\mathbb {P} _{X}(E)$，从而计算出 $\mathbb {P} (X\in E)$，对于任意集合 $E\in {\mathcal {F}}_{X}$。更一般地，为了计算概率 $\mathbb {P} (X\in B)$ 对于任意 $B\in {\mathcal {B}}$ ($B$ 不一定属于 ${\mathcal {F}}_{X}$)，我们注意到 $\{X\in B\}=\{X\in B\cap {\mathcal {X}}\}$，并且发现 $B\cap {\mathcal {X}}\in {\mathcal {F}}_{X}$。因此，我们可以通过考虑 $\mathbb {P} _{X}(B\cap {\mathcal {X}})$ 来计算 $\mathbb {P} (X\in B)$。

示例。 假设我们抛掷一枚公平的硬币两次。那么，样本空间可以用 $\{{\text{HH, HT, TH, TT}}\}$ 表示。现在，我们将随机变量 $X$ 定义为样本点抛掷中获得的正面数（这意味着 $X$ 将样本空间中的每个样本点映射到该样本点中获得的正面数）。那么，我们有 $${\begin{array}{ccccc}\omega &{\text{HH}}&{\text{HT}}&{\text{TH}}&{\text{TT}}\\\hline X(\omega )&2&1&1&0\\\end{array}}$$ 因此，$\{X=0\}=\{{\text{TT}}\},\{X=1\}=\{{\text{HT}},{\text{TH}}\},\{X=2\}=\{{\text{HH}}\}$。因此，我们有 $${\begin{array}{cccc}x&0&1&2\\\hline \mathbb {P} (X=x)&{\frac {1}{4}}&{\frac {2}{4}}&{\frac {1}{4}}\\\end{array}}$$ （样本空间中的四个结果应该是等概率的。）（通常用 $\mathbb {P} (X=x)$ 代替 $\mathbb {P} (\{X=x\})$，$\mathbb {P} (X\leq x)$ 代替 $\mathbb {P} (\{X\leq x\})$ 等等。）

练习。 假设我们抛掷一枚公平的硬币三次，并定义随机变量 $X$ 为样本点抛掷中获得的正面次数。那么，${\mathcal {X}}=\{0,1,2,3\}$。计算概率 $\mathbb {P} (X=x)$ 对于每个 $x\in {\mathcal {X}}$。因此，计算概率 $\mathbb {P} (X\leq x)$ 对于每个 $x\in {\mathcal {X}}$。(提示: 我们可以写 $\mathbb {P} (X\leq x)=\mathbb {P} (X\in (-\infty ,x])$。现在，考虑 $\mathbb {P} _{X}((-\infty ,x]\cap {\mathcal {X}})$。）

解答

首先，我们有 $${\begin{array}{ccccc}\omega &{\text{HHH}}&{\text{HHT}}&{\text{HTH}}&{\text{THH}}&{\text{TTH}}&{\text{THT}}&{\text{HTT}}&{\text{TTT}}\\\hline X(\omega )&3&2&2&2&1&1&1&0\\\end{array}}$$ 因此，我们有 $${\begin{array}{cccc}x&0&1&2&3\\\hline \mathbb {P} (X=x)&{\frac {1}{8}}&{\frac {3}{8}}&{\frac {3}{8}}&{\frac {1}{8}}\\\end{array}}$$ 由于 $\mathbb {P} (X\leq x)=\mathbb {P} _{X}((-\infty ,x]\cap {\mathcal {X}})=\mathbb {P} _{X}(\{0,1,\dotsc ,x\})=\sum _{y=0}^{x}\mathbb {P} _{X}(\{y\})=\sum _{y=0}^{x}\mathbb {P} (X=y)$，因此，我们有 $${\begin{array}{cccc}x&0&1&2&3\\\hline \mathbb {P} (X\leq x)&{\frac {1}{8}}&{\frac {4}{8}}&{\frac {7}{8}}&{\frac {8}{8}}\\\end{array}}$$

有时，即使不可能列出样本空间中的所有样本点，我们也可以确定与随机变量相关的概率。

示例。 考虑关于动机部分中讨论的民意调查的示例。我们将随机变量定义为给出“1”的数量。这里，我们假设样本空间中的每个样本点都是等可能的。证明 $\mathbb {P} (X=x)={\frac {\binom {100}{x}}{2^{100}}}$ 对于每个 $x\in {\mathcal {X}}=\{0,1,2,\dotsc ,100\}$。

证明。 由于有 ${\binom {100}{x}}$ 个样本点包含 $x$ 个“1”（将此视为将 $x$ 个不可区分的“1”放置到 100 个可区分的单元格中），结果随之而来。

$\Box$

备注。

• 例如，$\mathbb {P} (X=3)\approx 1.276\times 10^{-25}$，$\mathbb {P} (X=50)\approx 0.07958924$ 和 $\mathbb {P} (X=79)\approx 1.6107\times 10^{-9}$。
• 绘制不同 $x$ 值下 $\mathbb {P} (X=x)$ 的值。

一类非常有用的特殊随机变量是指示随机变量，它是 指示函数 的特例。

定义. （指示函数）

指示函数的图形说明。 “凸起部分” 是集合 $A$，整个红色正方形是集合 $X$。

集合 $X$ 的子集 $A$ 的指示函数是一个函数 $\mathbf {1} _{A}:X\to \{0,1\}$，定义为 $$\mathbf {1} _{A}(x)={\begin{cases}1&{\text{if }}x\in A\\0&{\text{if }}x\in X\setminus A.\end{cases}}$$

备注。

• 特例：我们可以通过稍微修改一下指示函数，将其视为一个随机变量。

• 设 $(\Omega ,{\mathcal {F}},\mathbb {P} )$ 为一个概率空间，而 $A\in {\mathcal {F}}$ 为一个事件。 然后，事件 $A$ 的指示随机变量是 $\mathbf {1} _{A}:\Omega \to \mathbb {R}$（这里，我们将陪域改为 $\mathbb {R}$，以符合随机变量的定义）定义为

$$\mathbf {1} _{A}(\omega )={\begin{cases}1&{\text{if }}\omega \in A\\0&{\text{if }}\omega \in \Omega \setminus A.\end{cases}}$$

示例： 假设我们从某个城市中随机选择一名市民，并记录该市民的年收入 $\omega$（以该城市使用的货币单位计）。在这种情况下，我们可以将样本空间定义为 $\Omega =[0,\infty )$。假设该城市制定了一项税收政策，规定年收入超过 10000（与 $\omega$ 相同的货币单位）则为 应税收入。现在，我们令 $X$ 表示记录的年收入的应税部分。更准确地说，$X:\Omega \to \mathbb {R}$ 定义为 $$X(\omega )={\begin{cases}0,&{\text{if }}\omega \leq 10000\\\omega -10000,&{\text{if }}\omega >10000.\end{cases}}$$，对于每个 $\omega \in \Omega$。也就是说，$X(\omega )=\max\{\omega -c,0\}$，表示为 $(\omega -c)_{+}$，对于每个 $\omega \in \Omega$。

示例。 假设我们掷两个不同的骰子，并定义 $X$ 为掷骰结果的数字之和。 那么，样本空间为 $\Omega =\{(1,1),(1,2),\dotsc ,(6,6)\}$。 这里我们可以看到 $X$ 的取值范围是 ${\mathcal {X}}=\{\underbrace {2} _{1+1},3,4,\dotsc ,\underbrace {12} _{6+6}\}$。 计算每个 $x\in {\mathcal {X}}$ 的 $\mathbb {P} (X=x)$。

解。 注意，在样本空间中，有 1、2、3、4、5、6、5、4、3、2、1 个样本点，分别对应于 $X=2,3,\dotsc ,12$。 因此，我们有 $${\begin{aligned}\mathbb {P} (X=2)&={\frac {1}{36}}\\\mathbb {P} (X=3)&={\frac {2}{36}}\\\mathbb {P} (X=4)&={\frac {3}{36}}\\\mathbb {P} (X=5)&={\frac {4}{36}}\\\mathbb {P} (X=6)&={\frac {5}{36}}\\\mathbb {P} (X=7)&={\frac {6}{36}}\\\mathbb {P} (X=8)&={\frac {5}{36}}\\\mathbb {P} (X=9)&={\frac {4}{36}}\\\mathbb {P} (X=10)&={\frac {3}{36}}\\\mathbb {P} (X=11)&={\frac {2}{36}}\\\mathbb {P} (X=12)&={\frac {1}{36}}.\\\end{aligned}}$$

练习。 计算 $\mathbb {P} (X\geq 8)$ 的概率。 (答案：${\frac {5}{12}}$)

解答

该概率为 $$\mathbb {P} (X\geq 8)=\mathbb {P} _{X}(\{8,9,10,11,12\})=\sum _{x=8}^{12}\mathbb {P} _{X}(\{x\})=\sum _{x=8}^{12}\mathbb {P} (X=x)={\frac {5+4+3+2+1}{36}}={\frac {5}{12}}.$$

累积分布函数

对于每个随机变量 $X$，都存在一个与之相关的函数，称为 累积分布函数 (cdf) 的 $X$

定义。

三个累积分布函数的例子，用红色线和点表示在两条蓝色线之间。

(累积分布函数) 随机变量 $X$ 的 累积分布函数 (cdf)，记为 $F_{X}(x)$ (或 $F(x)$) 是 $$F_{X}(x)=\mathbb {P} (X\leq x)$$ 对于每个 $x\in \mathbb {R}$。

示例。 考虑之前的一个练习，我们抛一枚公平的硬币三次，随机变量 $X$ 被定义为样本点中获得的正面次数。我们已经计算出 $\mathbb {P} (X\leq 0)={\frac {1}{8}},\quad \mathbb {P} (X\leq 1)={\frac {4}{8}},\quad \mathbb {P} (X\leq 2)={\frac {7}{8}},\quad \mathbb {P} (X\leq 3)={\frac {8}{8}}$。因此，随机变量 $X$ 的累积分布函数由 $$F_{X}(x)={\begin{cases}0,&{\text{if }}x<0\\{\frac {1}{8}},&{\text{if }}0\leq x<1\\{\frac {4}{8}},&{\text{if }}1\leq x<2\\{\frac {7}{8}},&{\text{if }}2\leq x<3\\{\frac {8}{8}},&{\text{if }}x\geq 3.\\\end{cases}}$$ 图表上，累积分布函数是一个阶梯函数，每个 $x\in {\mathcal {X}}=\{0,1,2,3\}$ 都有一个跳跃，跳跃的大小为 $\mathbb {P} (X=x)$。

累积分布函数中“跳跃”的示意图。

从上面的例子中的累积分布函数可以看出，累积分布函数不一定是连续的。在跳跃点处有几个不连续点。但我们可以注意到，在每个跳跃点，累积分布函数取跳跃的顶端的值，这是根据累积分布函数的定义（所涉及的不等式也包含等式）。简单来说，这表明累积分布函数是右连续的。但是，累积分布函数一般来说不是左连续的。

下面，我们将讨论累积分布函数的三个定义属性。

定理。（累积分布函数的定义属性）函数 $F$ 是随机变量 $X$ 的累积分布函数当且仅当

(i) $0\leq F(x)\leq 1$ 对于每个实数 $x$。

(ii) $F$ 是单调不减的。

(iii) $F$ 是右连续的。

证明。 充分性（$F$ 是累积分布函数 $\Rightarrow$ 这三个属性）

(i) 它遵循概率公理，因为 $F$ 被定义为概率。

(ii) $${\begin{aligned}x\leq y&\Rightarrow \{X\leq x\}\subseteq \{X\leq y\}\\&\Rightarrow \mathbb {P} (X\leq x)\leq \mathbb {P} (X\leq y)&\qquad {\text{by monotonicity}}\\&\Rightarrow F(x)\leq F(y)&\qquad {\text{by definition}}\\\end{aligned}}$$

(iii) 固定一个任意的正数列 $\epsilon _{1}>\epsilon _{2}>\cdots$，其中 $\lim _{n\to \infty }\epsilon _{n}=0$。对每个正数 $n$，定义 $E_{n}=\{X\leq x+\epsilon _{n}\}$。因此，$E_{1}\supset E_{2}\supset \cdots$。然后，$$\mathbb {P} (X\leq x)=\mathbb {P} \underbrace {\left(\lim _{n\to \infty }E_{n}\right)} _{\{X\leq x+0\}}=\mathbb {P} \left(\lim _{n\to \infty }E_{1}\cap E_{2}\cap \cdots E_{n}\right)=\lim _{n\to \infty }\mathbb {P} (E_{1}\cap \cdots \cap E_{n})=\lim _{n\to \infty }\mathbb {P} (E_{n})=\lim _{n\to \infty }\mathbb {P} (X\leq x+\epsilon _{n})$$ 因此 $$F(x)=\lim _{n\to \infty }F(x+\epsilon _{n})$$ 对每个 $\epsilon _{1}>\epsilon _{2}>\cdots$ 其中 $\epsilon _{n}\to 0$ 当 $n\to \infty$。也就是说，$$\lim _{h\to 0^{+}}F(x+h)=F(x)$$，这就是右连续性的定义。

如果部分更复杂。以下内容是可选的。概述

1. 绘制任意一条满足这三个性质的曲线。
2. 无限次抛掷一枚公平的硬币。
3. 将每次结果编码成二进制数，例如 $HHT\cdots \to 0.110\ldots$
4. 将每个二进制数转换为十进制数，例如$0.110\ldots \to 1(2^{-1})+1(2^{-2})=0.75\ldots$。然后，十进制数是一个随机变量$U\in [0,1]$。
5. 使用此十进制数作为任意绘制曲线反函数的输入，我们得到一个值，该值也是一个随机变量，比如$X$。
6. 然后，我们得到了随机变量$X$ 的累积分布函数$F(x)=\mathbb {P} (X\leq x)=\mathbb {P} (U\leq F(x))$，如果我们无限次地抛一枚公平的硬币。

$\Box$

有时，我们只对$x$ 这样使得$\mathbb {P} (X=x)\neq 0$ 的值感兴趣，这些值更为“重要”。粗略地说，这些值实际上是$X$ 的支撑集 的元素，该集合将在下文中定义。

定义。（随机变量的支撑集）随机变量$X$ 的支撑集，$\operatorname {supp} (X)$，是最小的闭集$S$，使得$\mathbb {P} (X\in S)=1$。

备注。

• 例如，闭区间是闭集。
• 本书不会重点强调闭合性。
• 实际上，$\operatorname {supp} (X)=\{x\in \mathbb {R} :f(x)>0\}$（这是最小的闭集）。

• $f(x)$ 是离散随机变量的概率质量函数；
• $f(x)$ 是连续随机变量的概率密度函数。
• 上述术语将在后面定义。

示例. 如果 $$\mathbb {P} (X=x)={\begin{cases}1/4,\quad &x=0;\\1/8,\quad &x=3;\\5/8,\quad &x=6;\\0&{\text{otherwise}},\\\end{cases}}$$ 那么 $\operatorname {supp} (X)=\{0,3,6\}$，因为 $\mathbb {P} (X\in \{0,3,6\})=1$，并且该集合是满足此要求的所有集合中最小的集合。

备注. $\mathbb {R} ,\{0,1,2,3,4,5,6\},$等等也满足要求，但它们不是最小的集合。

练习。

假设我们抛掷一枚不公平的硬币。定义 $X=1$ 如果正面朝上， $X=-1$ 否则。令 $F(x)$ 为 $X$ 的累积分布函数。

1 求 $\operatorname {supp} (\mathbf {1} \{X=1\})$。

	$\{-1,1\}$
	$\{0,1\}$
	$\{\mathbf {1} \{X=1\}=0,\mathbf {1} \{X=1\}=1\}$
	由于没有给出正面朝上的概率，因此无法确定。

2 假设 $\mathbb {P} (X=1)=0.7$，计算 $F(0)$。

	0
	0.3
	0.5
	0.7
	1

3 假设 $\mathbb {P} (X=1)=p\in (0,1)$。以下哪些陈述是正确的？

	$F(1)=1$
	$F(-1)=0$
	$F(0)+F(-1)=F(1)$
	$F(1)=2F(0.5)$ 如果硬币是公平的。
	$\lim _{x\to -1^{-}}F(x)=F(-1)$

离散随机变量

定义。 （离散随机变量） 如果 $\operatorname {supp} (X)$ 是 可数的 （即“可枚举的”或“可列出的”），则随机变量 $X$ 是一个 离散 随机变量。

例子。 令 $X$ 是 $n$ 次伯努利试验中成功的次数。 那么，$X$ 是一个离散随机变量，因为 $\operatorname {supp} (X)=\{0,1,\ldots ,n\}$ 是可数的。

另一方面，如果我们让 $Y$ 是摄氏温度，$Y$ 不是离散的，因为 $\operatorname {supp} (Y)=[\underbrace {-273.15} _{\text{absolute zero}},\underbrace {1.417\times 10^{32}} _{\text{Planck temperature}}]$ 是不可数的。

练习。

以下哪些是（是）离散随机变量？

	抛掷一枚硬币三次出现的正面次数。
	介于 0 和 1 之间（包括 0 和 1）的数字。
	多项选择题中正确选项的数量，其中最多有三个正确选项。
	对要求数值答案的简短问题的答案。
	随机变量为离散随机变量的概率。

通常，对于离散随机变量，我们感兴趣的是随机变量取特定值的概率。因此，我们有一个函数可以给出每个特定值所对应的概率，即 概率质量函数。

定义。

pmf 的一个例子。该函数称为概率质量函数，因为每个点的值可以解释为位于该点的点的质量。

(概率质量函数) 令 $X$ 为离散随机变量。 $X$ 的概率质量函数 (pmf) 是 $$f({\color {green}x})=\mathbb {P} (X={\color {green}x}).$$

备注。

• 其他名称包括质量函数和概率函数。
• 如果随机变量 $X$ 是离散的，那么 $\operatorname {supp} (X)=\{x\in \mathbb {R} :f(x)>0\}$ (它是封闭的)。
• 随机变量 $X$ 的累积分布函数 (cdf) 为 $F(x)=\mathbb {P} (X\leq x)=\sum _{\{y:y\leq x\}}f(y)$。 因此，pmf 在支持内每个 $x$ 处的值的总和等于 1。
• 离散随机变量 $X$ 的 cdf 是一个阶梯函数，在 $\operatorname {supp} (X)$ 中的点处跳跃，每个跳跃的大小定义了 $X$ 在 $\operatorname {supp} (X)$ 中对应点的 pmf。

例如。 假设我们掷一个公平的六面骰子一次。 令 $X$ 为朝上的数字。 那么，$X$ 的 pmf 是 $$f(x)={\begin{cases}1/6,\quad &x=1,2,3,4,5{\text{ or }}6;\\0&{\text{otherwise}}.\end{cases}}$$

练习。

1 以下哪些是 (是) pmf？

	$f(x)={\begin{cases}1/2^{n},\quad &n\in \mathbb {N} \\0&{\text{otherwise}}\end{cases}}$. 给定$\mathbb {N} =\{1,2,\ldots \}$是可数的。
	$f(x)={\begin{cases}1,\quad &0\leq x\leq 1\\0&{\text{otherwise}}\end{cases}}$
	$f(x)={\begin{cases}0.2,\quad &x=2\\0.3,\quad &x=6\\0.4,\quad &x=8\\0&{\text{otherwise}}\end{cases}}$
	$f(x)={\begin{cases}0.2,\quad &x=2\\0.3,\quad &x=6\\0.4,\quad &x=8\\0.1&{\text{otherwise}}\end{cases}}$
	$f(x)={\frac {\mathbf {1} \{x=2\cup x=3\cup x=4\}}{3}}$

2 计算$k$，使得函数$f(x)=\mathbf {1} \{x=k\}k+2(\mathbf {1} \{x=2k\}k)+3(\mathbf {1} \{x=3k\}k)$ 是一个概率质量函数。

	$1/12$
	$1/6$
	$1/3$
	$1$

连续随机变量

假设 $X$ 是一个离散随机变量。将 $S$ 分割成小的不相交的区间 $[x_{1},x_{1}+\Delta x_{1}],\dotsc$ 得出 $$\mathbb {P} (X\in S)=\mathbb {P} \left(X\in \bigcup _{i}[x_{i}+\Delta x_{i}]\right)=\sum _{i}\mathbb {P} {\big (}X\in [x_{i}+x_{i}+\Delta x_{i}]{\big )}=\sum _{i}\underbrace {\frac {\mathbb {P} {\big (}X\in [x_{i}+x_{i}+\Delta x_{i}]{\big )}}{\Delta x_{i}}} _{\text{probability per unit}}\cdot \Delta x_{i}.$$ 特别地，每单位的概率可以被解释为 $X$ 在该区间上的概率密度。(密度越高，分配给该区间的概率就越多)。

取极限，$$\lim _{\Delta x_{i}\to 0}\sum _{i}\underbrace {\frac {\mathbb {P} {\big (}X\in [x_{i}+x_{i}+\Delta x_{i}]{\big )}}{\Delta x_{i}}} _{\text{density}}\cdot \Delta x_{i}=\int _{S}\underbrace {f(x)} _{\text{density}}\,dx,$$ 其中，直观且非严格地，$f(x)\,dx$ 可以理解为在“无穷小”区间 $[x,x+dx]$ 上的概率，即 $\mathbb {P} (X\in [x,dx])$，而 $f(x)$ 可以理解为在这个“无穷小”区间上的概率密度，即 ${\frac {\mathbb {P} (X\in [x,dx])}{dx}}$.

这些促使我们给出如下定义。

定义. (连续型随机变量) 随机变量 $X$ 为 连续型，如果对于每个（可测）集合 $S\subseteq \mathbb {R}$ 以及某个 非负 函数 $f$，有 $$\mathbb {P} (X\in S)=\int _{S}f(x)\,dx$$ 成立。

备注。

• 函数 $f$ 被称为 概率密度函数 (pdf)，密度函数，或概率函数（很少见）。
• 如果 $X$ 为连续型，则 pdf 在每个 单点值 上的值为零，即 $\mathbb {P} (X=x)=0$ 对每个实数 $x$ 成立。

• 可以通过设置 $S=\{x\}$ 来证明这一点，则 $\int _{S}f(u)\,du=\int _{x}^{x}f(u)\,du=0$（哑变量已更改）。

• 通过设置 $S=(-\infty ,x]$，累积分布函数 $F(x)=\mathbb {P} {\big (}X\in (-\infty ,x]{\big )}=\int _{-\infty }^{x}f(u)\,du$。
• 可测性不会被强调。本书中遇到的集合都是可测的。
• $\int _{S}f(x)\,dx$ 是 pdf 在 $S$ 下的面积，它表示概率（通过将密度函数在集合 $S$ 上积分得到的）。

名称 连续 随机变量来自这样的结果，即这种随机变量的累积分布函数是连续的。

命题。（连续随机变量的累积分布函数的连续性）如果随机变量 $X$ 是连续的，它的累积分布函数 $F$ 也是连续的（不仅仅是右连续）。

证明。 由于 $\lim _{h\to 0}F(x+h)=\lim _{h\to 0}\int _{-\infty }^{x+h}f(u)\,du=\int _{-\infty }^{x}f(x)\,dx=F(x)$（黎曼积分是连续的），累积分布函数是连续的。

$\Box$

示例。（指数分布）函数 $F(x)=(1-e^{-\lambda x})\mathbf {1} \{x\geq 0\}$ 是连续随机变量的累积分布函数，因为

• 它是非负的。
• $\int _{-\infty }^{\infty }(1-e^{-\lambda x})\mathbf {1} \{x\geq 0\}\,dx=\int _{0}^{\infty }(1-e^{-\lambda x})\,dx=1-(1-\underbrace {e^{0}} _{1})=1$. 因此，$\lim _{x\to \infty }F(x)=1$.
• 它是不减的。
• 它是右连续的（也是连续的）。

练习。

1 以下哪些是概率密度函数（PDF）？

	$f(x)=\mathbf {1} \{x\geq 0\}/x$
	$f(x)=\mathbf {1} \{x\geq 0\}/x^{2}$
	$f(x)=\mathbf {1} \{3\leq x\leq 8\}/5$
	$f(x)=\mathbf {1} \{0\leq x\leq 1\}x$
	$f(x)=\mathbf {1} \{0\leq x\leq {\sqrt {2}}\}({\sqrt {2}}-x)$

2 计算 $k$ 使得函数 $f(x)=k\mathbf {1} \{0\leq x\leq k/4\}x$ 为概率密度函数。

	$1$
	$2^{1/3}$
	${\sqrt {2}}$
	$2$
	不存在这样的 $k$.

3 计算 $k$ 使得函数 $F(x)=k\mathbf {1} \{0\leq x\leq k/4\}x$ 是一个累积分布函数。

	$1$
	$2^{1/3}$
	${\sqrt {2}}$
	$2$
	不存在这样的 $k$.

4 以下哪些是正确的？

	如果一个随机变量的支撑集是可数的，那么它是离散的。
	如果一个随机变量的支撑集是不可数的，那么它是连续的。
	如果一个随机变量的支撑集是不可数的，那么它不是离散的。

命题。 (用累积分布函数求概率密度函数) 如果连续随机变量的累积分布函数 $F(x)$ 可微，那么概率密度函数 $f(x)=F'(x)$.

证明。 这是由微积分基本定理得到的：$$F'(x)={\frac {d}{dx}}\int _{-\infty }^{x}f(u)\,du=f(x).$$

$\Box$

备注。 由于 $F(x)$ 是单调不减的，$F'(x)\geq 0\Rightarrow f(x)\geq 0$。 这表明如果 $F$ 可微，则 $f(x)$ 始终是非负的。 这是我们定义概率密度函数为非负的动机。

在没有进一步假设的情况下，概率密度函数 不 是唯一的，即一个随机变量可能有多个概率密度函数，例如，我们可以在其支撑集之外的单个点上将概率密度函数的值设置为一个实数（不会影响概率，因为概率密度函数在单个点的值为零，无论其值如何），这将为一个随机变量创建另一个有效的概率密度函数。 为了解决这个问题，我们通常将 $f(x)=0$ 设置为每个 $x\notin \operatorname {supp} (X)$，以使概率密度函数变得唯一，并使计算更方便。

示例：（均匀分布）已知 $$f(x)=\mathbf {1} \{1\leq x\leq 5\}/4$$ 是连续随机变量 $X$ 的概率密度函数，则概率 ${\displaystyle \mathbb {P} (2$

练习。

已知函数 $f(x)=\mathbf {1} \{1\leq x\leq 6\}e^{x}/(e^{6}-e)$ 是连续随机变量 $X$ 的概率密度函数。

1 计算 $\mathbb {P} (X>3)$.

	${\frac {e^{6}-e^{3}}{e^{6}-e}}$
	${\frac {e^{3}-e}{e^{6}-e}}$
	${\frac {e^{3}}{e^{6}-e}}$
	$e^{3}-e$
	$e^{6}-e^{3}$

2 计算 $\mathbb {P} (X>3|X<4)$.

	${\frac {e^{4}-e}{e^{4}-e^{3}}}$
	${\frac {e^{3}-e}{e^{4}-e^{3}}}$
	${\frac {e^{4}-e^{3}}{e^{4}-e}}$
	${\frac {e^{3}-e}{e^{4}-e}}$
	$1$

3 计算 $\mathbb {P} (X>3|X\geq 4)$.

	$1-{\frac {e^{4}-e}{e^{4}-e^{3}}}$
	$1-{\frac {e^{3}-e}{e^{4}-e^{3}}}$
	$1-{\frac {e^{4}-e^{3}}{e^{4}-e}}$
	$1-{\frac {e^{3}-e}{e^{4}-e}}$
	$0$

混合随机变量

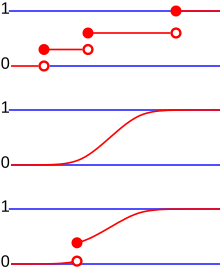
在阅读了前两节之后，你可能会认为随机变量要么是离散的，要么是连续的。实际上，这是错误的。随机变量可以既不是离散的也不是连续的。这种随机变量的一个例子是本节讨论的 混合 随机变量。

定理。 (cdf 分解) 每个随机变量 $X$ 的 cdf $F(x)$ 可以分解为三个部分的总和： $$F(x)=\alpha _{d}F_{d}(x)+\alpha _{c}F_{c}(x)+\alpha _{s}F_{s}(x)$$ 其中 $\alpha _{d},\alpha _{c},\alpha _{s}$ 是非负常数，使得 $\alpha _{d}+\alpha _{c}+\alpha _{s}=1$，其中 $x$ 是一个实数，$F_{d},F_{c},F_{s}$ 分别是离散、连续和奇异随机变量的 cdf。

备注。

• 如果 $\alpha _{d}\neq 0$ 且 $\alpha _{c}\neq 0$，则 $X$ 是一个混合随机变量。
• 我们不会在本书中讨论奇异随机变量，因为它比较高级。
• 这个公式的一种解释是： $$X={\begin{cases}{\text{discrete random variable having cdf }}F_{d}{\text{ with probability }}\alpha _{d};\\{\text{continuous random variable having cdf }}F_{c}{\text{ with probability }}\alpha _{c};\\{\text{singular random variable having cdf }}F_{s}{\text{ with probability }}\alpha _{s}.\end{cases}}$$
• 如果 $X$ 是离散（连续）随机变量，那么 $\alpha _{c}=\alpha _{s}=0$ ($\alpha _{d}=\alpha _{s}=0$ )。
• 我们也可以类似地分解pdf，但我们有不同的方法从相应的cdf中找到离散和连续随机变量的pdf。

奇异随机变量的一个例子是 康托尔分布函数（有时称为魔鬼的楼梯），如下图所示。当您放大图形时，图形模式会不断重复。

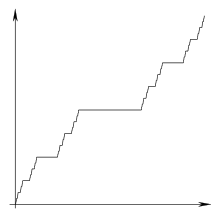康托尔分布函数

例： 令 $F_{d}(x)={\frac {1}{3}}\mathbf {1} \{x\geq 3\}+{\frac {2}{3}}\mathbf {1} \{x\geq 7\}$。令 $F_{c}(x)=\mathbf {1} \{x\geq 1\}(x-1)/(x+1)$。那么，$F(x)=(1/2)F_{d}(x)+(1/2)F_{c}(x)$ 是一个混合随机变量 $X$ 的 cdf，它以概率 $1/2$ 为离散，以概率 $1/2$ 为连续，因为它是非负的、非递减的、右连续的，并且 $\lim _{x\to \infty }F(x)=(1/2)\left[\lim _{x\to \infty }(F_{d}(x)+F_{c}(x)\right]=(1/2)(1+1)=1$。

练习： 考虑函数 $F(x)={\frac {\mathbf {1} \{x\geq 8\}+(1-1/x)\mathbf {1} \{x\geq 1\}}{k}}$。已知 $F(x)$ 是随机变量 $X$ 的 cdf。

(a) 证明 $k=2$。

(b) 证明 $X$ 的 pdf 为 $$f(x)={\frac {1}{2}}(\mathbf {1} \{x=8\}+x^{-2}\mathbf {1} \{x\geq 1\}).$$

(c) 证明 $X$ 为连续型随机变量的概率为 $1/k$。

(d) 证明 $\mathbb {P} (X\geq 3|X\leq 8)$ 等于 $2/3$。

(e) 证明事件 $\{X\geq 3\}$ 和 $\{X\leq m\}$ 在 $m\geq 8$ 时相互独立。

证明。

(a) 由于 $F$ 是累积分布函数，且当 $x\to \infty$ 时，$\mathbf {1} \{x\geq 8\}=\mathbf {1} \{x\geq 1\}=1$，因此，$$\lim _{x\to \infty }F(x)=1\implies {\frac {1+1}{k}}=1\implies k=2.$$

(b) 由于 $X$ 是混合型随机变量，对于离散型随机变量部分，概率密度函数为 $$f_{d}(x)=\mathbf {1} \{x=8\}/2.$$ 另一方面，对于连续型随机变量部分，概率密度函数为 $$f_{c}(x)=\mathbf {1} \{x\geq 1\}x^{-2}/2.$$ 因此，$X$ 的概率密度函数为 $$f(x)={\frac {1}{2}}(\mathbf {1} \{x=8\}+x^{-2}\mathbf {1} \{x\geq 1\})$$

(c) 可以看到 $F(x)$ 可以分解如下：$$F(x)={\frac {1}{2}}(\mathbf {1} \{x\geq 8\})+{\frac {1}{2}}((1-1/x)\mathbf {1} \{x\geq 1\}).$$ 因此，$X$ 为连续变量的概率为 $1/k=1/2$。

(d) $$\mathbb {P} (X\geq 3|X\leq 8)={\frac {\mathbb {P} (3\leq X\leq 8)}{\mathbb {P} (X\leq 8)}}={\frac {\mathbb {P} (X\leq 8)-\mathbb {P} (X\leq 3)+\overbrace {\mathbb {P} (X=3)} ^{0}}{1}}=1-\overbrace {(1-1/3)/2} ^{1/3}=2/3.$$

(e) 如果 $m\geq 8$，$\mathbb {P} (X\leq m)=1$。 因此，$$\mathbb {P} (X\geq 3\cap X\leq m)=\mathbb {P} (X\leq m)-\mathbb {P} (X\leq 3)+\underbrace {\mathbb {P} (X=3)} _{0}=1-\mathbb {P} (X\leq 3)=\mathbb {P} (X>3)=\mathbb {P} (X>3)+\underbrace {\mathbb {P} (X=3)} _{0}=\mathbb {P} (X\geq 3)=\mathbb {P} (X\geq 3)\underbrace {\mathbb {P} (X\leq m)} _{1},$$ 也就是说 $\{X\geq 3\}$ 和 $\{X\leq m\}$ 是相互独立的。

$\Box$