信号与系统/工程函数

信号与系统

基本函数

通常，复杂的信号可以简化为某些基本函数的线性组合（傅立叶分析中的一个关键概念），这在工程领域很有用。这些函数将在本文档中进行描述，并在后续章节中进行更详细的探讨。

单位阶跃函数

单位阶跃函数和冲激函数被认为是工程学中的基本函数，强烈建议读者熟悉这两个函数。

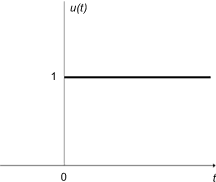单位阶跃函数，也称为Heaviside 函数，定义如下：

u(t)=\left\{{\begin{matrix}0,&{\mbox{if }}t<0\\1,&{\mbox{if }}t\geq 0\end{matrix}}\right.

有时，u(0) 会被赋予其他值，通常是 0 或 1。对于许多应用来说，零点处的取值无关紧要。u(0) 通常被写为未定义。

导数

单位阶跃函数在除 t = 0 处的间断点外，所有地方都是水平的。因此，单位阶跃函数的导数在所有点 t 处都为 0，除了 t = 0。在 t = 0 处，单位阶跃函数的导数是无穷大。

单位阶跃函数的导数称为冲激函数。冲激函数将在下一节中更详细地描述。

积分

单位阶跃函数的积分计算如下：

\int _{-\infty }^{t}u(s)ds=\left\{{\begin{matrix}0,&{\mbox{if }}t<0\\\int _{0}^{t}ds=t,&{\mbox{if }}t\geq 0\end{matrix}}\right\}=tu(t)

换句话说，单位阶跃函数的积分是一个“斜坡”函数。该函数对于所有小于零的值都为零，并且从零开始变成一条斜率为 +1 的直线。

时间反转

如果我们要反转单位阶跃函数，我们可以像这样将其绕着 y 轴翻转：u(-t)。经过一些操作，我们可以得到一个重要的结果：

u(-t)=1-u(t)

, 同时

t\neq 0

其他属性

这里我们将列出单位阶跃函数的一些其他属性：

$u(\infty )=1$
$u(-\infty )=0$
$u(t)+u(-t)=1$ , 同时 $t\neq 0$

这些都是重要的结果，读者应该熟悉它们。

冲激函数

冲激函数是一个特殊的函数，工程师经常用它来模拟某些事件。冲激函数是不可实现的，因为根据定义，冲激函数的输出在某些值上是无穷大的。冲激函数也称为“狄拉克函数”，尽管存在不同类型的狄拉克函数，它们各自具有略微不同的属性。具体来说，这种单位冲激函数被称为狄拉克 delta 函数。术语“冲激函数”是明确的，因为“冲激”一词只有一个定义。

让我们从绘制一个矩形函数 D(t) 开始，如下所示

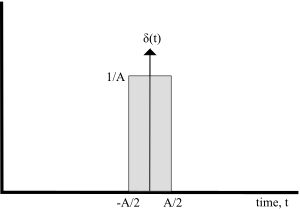
我们可以用单位阶跃函数来定义这个矩形

D(t)={\frac {1}{A}}[u(t+A/2)-u(t-A/2)]

现在，我们想分析这个矩形，当 A 变得无穷小的时候。我们可以用这个矩形来定义这个新函数，即狄拉克函数

\delta (t)=\lim _{A\to 0}{\frac {1}{A}}[u(t+A/2)-u(t-A/2)]

我们可以用分段的方式类似地定义狄拉克函数，如下所示

$\delta (t)=0{\mbox{ for }}t\neq 0$ .
$\delta (t)=+\infty {\mbox{ for }}t=0$ .
$\int _{-\infty }^{\infty }\delta (t)dt=1$ .

虽然，这个定义不如之前的定义严谨。

积分

从它的定义可以得出，冲激函数的积分就是阶跃函数

\int \delta (t)dt=u(t)

因此，将单位阶跃函数的导数定义为冲激函数是合理的。

平移性质

此外，对于可积函数 f

\int _{-\infty }^{\infty }\delta (t-A)f(t)dt=f(A)

这被称为狄拉克函数的平移性质（也称为筛选性质或采样性质）；它有效地对函数 f 在位置 A 处的值进行采样。

狄拉克函数在工程中有很多应用，其中最重要的应用之一是将连续函数采样为离散值。

利用这个性质，我们可以通过乘以一个冲激，然后积分，从连续函数中提取一个单一的值。

狄拉克函数的类型

有一些不同的函数都被称为“狄拉克函数”。这些函数通常都像一个冲激，但有一些区别。一般来说，本书使用“狄拉克函数”一词来指代狄拉克 delta 函数。

Sinc 函数

在通信工程中，有一种形式出现得非常频繁，因此我们给它起了一个自己的名字。这个函数叫做“Sinc 函数”，将在下面讨论。

Sinc 函数定义如下

\operatorname {sinc} (x)={\frac {\sin(\pi x)}{\pi x}}{\mbox{ if }}x\neq 0

和

\operatorname {sinc} (0)=1

sinc(x) 的值在 x = 0 处定义为 1，因为

\lim _{x\rightarrow 0}\operatorname {sinc} (x)=1

.

这个事实可以通过注意到 x 接近 0 时，

1>{\frac {\sin {(x)}}{x}}>\cos {(x)}

.

由于 cos(0) = 1，我们可以应用夹逼定理来证明当 x 趋近于零时，sinc 函数趋近于 1。因此，将 sinc(0) 定义为 1 使 sinc 函数连续。

此外，当 x 趋近于无穷大时，Sinc 函数趋近于零，且 sinc(x) 的包络以 1/x 的速度衰减。

矩形函数

矩形函数是一个产生以 t = 0 为中心，宽度为 1 的矩形脉冲的函数。矩形脉冲的高度也为 1。Sinc 函数和矩形函数构成傅里叶变换对。

矩形函数可以写成以下形式

\operatorname {rect} \left({\frac {t-X}{Y}}\right)

其中，脉冲以 X 为中心，宽度为 Y。我们可以通过将脉冲中心设置为零 (X = 0)，高度设置为 1/A，宽度设置为 A（趋近于零）来根据矩形函数定义上面的冲激函数

\delta (t)=\lim _{A\to 0}{\frac {1}{A}}\operatorname {rect} \left({\frac {t-0}{A}}\right)

我们也可以用一对单位阶跃函数构造矩形函数

\operatorname {rect} \left({\frac {t-X}{Y}}\right)=u(t-X+Y/2)-u(t-X-Y/2)

在这里，两个单位阶跃函数都设置在距 (t - X) 中心点 Y/2 的距离处。

方波

方波是一系列矩形脉冲。以下是一些方波的示例


这两个方波具有相同的幅度，但第二个方波的频率较低。我们可以看到，第二个方波的周期大约是第一个方波的两倍，因此第二个方波的频率大约是第一个方波频率的一半。


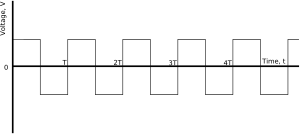
这两个方波具有相同的频率和相同的峰峰值幅度，但第二个方波没有直流偏移。请注意，第二个方波以x轴为中心，而第一个方波完全位于x轴上方。