信号与系统/Z 变换简介

采样系统

数字信号本质上是采样信号。在电路节点中，数字以给定的速率变化：采样速率或采样频率。信号两次变化之间的时间是采样频率的倒数：它是采样周期。

在处理器系统中，样本存储在内存中。在逻辑电路中，它们对应于寄存器输出。采样周期用于计算系统中所有信号的下一个值。

数字电路不是唯一的采样系统：诸如开关电容滤波器之类的模拟电路也依赖于开关，因此也被采样。

对信号进行采样

奈奎斯特速率

对信号进行采样提出了一个主要问题：在这个过程中是否会丢失信息？

例子

例子：每小时检查（=采样）一次交通信号灯肯定会让人对它们的信号反应迟钝（=丢失信息）。

另一方面，每微秒采样一次交通信号灯并不会比每毫秒采样一次带来更多信息。

显然，交通信号灯，像任何其他信号一样，必须以比其变化更快的速率进行采样，但以更快的速率采样它们并不会带来更多信息。

奈奎斯特速率是为了避免信息丢失而所需的最低采样速率。

f_{N}\ {\stackrel {\mathrm {def} }{=}}\ 2f_{b}

其中 $f_{b}$ 是要采样的信号的最高频率，也称为带宽。

为了避免丢失信息，采样速率必须高于奈奎斯特速率

f_{s}>f_{N}

在实践中，采样速率是通过一定的裕量来确定的，以便更轻松地重建原始信号。

例子

例子：音频内容采样速率

人类听觉的全部范围在 20 赫兹到 20 千赫兹之间。因此，音频内容必须以超过 40 千赫兹的速率进行采样。

事实上

CD 音频以 44.1 千赫兹的速率对信号进行采样。
专业数字视频设备以 48 千赫兹的速率对它们进行采样。
DVD 音频以 96 千赫兹的速率对它们进行采样。
高端 DVD 音频将该频率翻倍至 192 千赫兹。

混叠

以低于奈奎斯特速率的速率对信号进行采样会产生混叠或折叠。

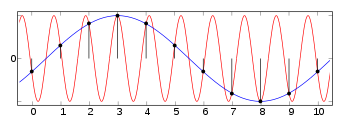
右图显示了一个频率为 0.9（因此周期接近 1.1）的红色正弦波。此信号应该以高于 1.8 的频率进行采样。但是，信号是以 1 的速率进行采样的（垂直线和黑点）。如果尝试在样本之间绘制一条线，结果将看起来像蓝色曲线，该曲线是周期为 10 或频率为 0.1 的正弦波。

如果信号以 0.9 的速率进行采样，采样点将始终落在正弦函数中的同一点，并且生成的信号将看起来像一个常数。

以 1 的速率对频率为 0.9 的信号进行采样会创建一个频率为 $1-0.9=0.1$ 的混叠。

以 0.9 的速率对频率为 0.9 的信号进行采样会创建一个直流混叠，因此频率为 $0.9-0.9=0$ 。

以 0.8 的速率对频率为 0.9 的信号进行采样也会创建一个频率为 $0.9-0.8=0.1$ 的混叠，但相位不同。

例子

例子：频闪灯是一个众所周知的混叠例子。

用以 100 赫兹频率切换的频闪灯照亮一个以 90 赫兹频率旋转的电机，会让我们觉得它以 100 赫兹 - 90 赫兹 = 10 赫兹的频率旋转。

用以 90 赫兹频率切换的频闪灯照亮一个以 90 赫兹频率旋转的电机，会让我们觉得它静止不动。

用以 80 赫兹频率切换的频闪灯照亮一个以 90 赫兹频率旋转的电机，会让我们觉得它以 90 赫兹 - 80 赫兹 = 10 赫兹的频率旋转，但方向相反。

这与许多美国西部电影中出现的驿马车场景中看到的现象相同。在不同的旋转速度下，驿马车上的车轮看起来会向前旋转、静止不动或向后旋转。参见车轮效应。

就好像信号的频谱在等于采样频率一半的点处被折叠回去了。

欠采样

以低于奈奎斯特速率的频率进行采样，也称为欠采样，会在较低的频率处创建正弦波混叠。如果原始信号在这些较低的频率处也存在内容，那么它们将混合在一起，并且会丢失信息。

但是，如果信号只包含高频内容，那么欠采样过程会以较低的频率对信号进行调制。

这是一种使用乘以调制正弦波的方式进行调制的廉价替代方案。

过采样

过采样对应于以远高于奈奎斯特频率（通常为奈奎斯特频率的 100 到 1000 倍）进行采样。过采样的目的是能够用更少的位数来表示信号。

这可以通过用于恢复额外位的机制来解释：只要新的采样频率大于奈奎斯特频率，以 10 kHz 采样的信号就可以以 5 kHz 进行降采样。降采样意味着样本数量减少一半。而不是丢弃每隔一个样本，可以计算两个连续样本的平均值，并使用该结果来构建新信号的一个样本。计算平均值对应于将值相加并除以二。而不是将结果除以二并丢弃小数点后的位，可以仅将连续样本两两相加。这样，5 kHz 信号的幅度是原始 10 kHz 信号的两倍。换句话说，它需要用多 1 位来表示。

过采样一个广泛应用的应用是脉冲宽度调制 (PWM)。调制信号用一个以 ${2^{n}}\cdot f_{N}$ 频率切换的单个位表示，其中 $f_{N}$ 是原始信号的奈奎斯特频率，而 $n$ 是用于表示它的位数。这个单比特信号非常适合用单个电源开关驱动大电流负载。PWM 通常用于驱动电动机。

在每个 CD 播放机中都可以找到一个用于单比特结果的更复杂的编码方案：Σ-Δ 调制。理解它的工作原理需要更多的理论知识。我们只说明它能够在比 PWM 更低的采样频率下用单个位表示信号。另一方面，单比特信号在它的采样频率下更频繁地来回切换，因此不适合驱动较慢的大电流开关。Σ-Δ 调制用于驱动更轻的负载，例如 CD 播放机和音频放大器之间的电缆。

例子

示例：超级音频光盘 (SACD)

SACD 以直接流数字信号的形式对音频进行编码，该信号以单个位编码，是 CD 44.1 kHz 采样率的 64 倍。