在接下来的内容中,我们将提供一些关于数值优化算法的笔记。由于存在大量方法 ,我们将限制自己讨论所谓的梯度方法 。我们之所以将此类方法作为数值优化算法的自然起点,主要有以下两个原因。一方面,这些方法在该领域确实是主力军,因此它们在实践中的频繁使用证明了它们在这里被讨论的合理性。另一方面,这种方法非常直观,因为它在一定程度上是自然地从众所周知的最优点性质 中推导出来的。我们将重点关注此类方法的三个例子:牛顿法 、最速下降法 以及可变度量法 ,其中包括拟牛顿法 。
在我们开始之前,我们还是要强调一点,似乎并没有一个“唯一”的算法,特定算法的性能总是取决于待解决的具体问题。因此,经验和“试错”在应用工作中非常重要。为了阐明这一点,我们将提供一些应用示例,其中可以通过图形方式比较不同算法的性能。此外,最后还提供了一个关于最大似然估计 的具体示例。对于统计学家和计量经济学家 来说,最大似然估计可能是在实践中必须依赖数值优化算法的最重要示例。
任何数值优化算法都需要解决找到函数的“可观察”属性的问题,以便计算机程序知道何时达到解。由于我们正在处理优化问题,因此两个众所周知的结果似乎是寻找这些属性的合理起点。
如果 f 可微且 x ⋆ {\displaystyle x^{\star }}
( 1 a ) D f ( x ⋆ ) = 0 {\displaystyle (1a)\quad Df(x^{\star })=0}
即雅可比矩阵 D f ( x ) {\displaystyle Df(x)}
以及
如果 f 二阶可微且 x ⋆ {\displaystyle x^{\star }}
( 1 b ) x T D 2 f ( x ⋆ ) x ≥ 0 {\displaystyle (1b)\quad x^{T}D^{2}f(x^{\star })x\geq 0}
即海森矩阵 D 2 f ( x ) {\displaystyle D^{2}f(x)} 正半定 的。
在下文中,我们将始终用 x ⋆ {\displaystyle x^{\star }} x ⋆ {\displaystyle x^{\star }} x ⋆ {\displaystyle x^{\star }} f {\displaystyle f} g ( f ( x ⋆ ) ) {\displaystyle g(f(x^{\star }))} x ⋆ {\displaystyle x^{\star }} f ( x ) = x 3 {\displaystyle f(x)=x^{3}} D f ( 0 ) = D 2 f ( 0 ) = 0 {\displaystyle Df(0)=D^{2}f(0)=0} x ⋆ ≠ 0 {\displaystyle x^{\star }\neq 0} x ⋆ {\displaystyle x^{\star }}
如果 D f ( x ⋆ ) = 0 {\displaystyle Df(x^{\star })=0} x T D 2 f ( z ) x ≥ 0 , ∀ x ∈ R n {\displaystyle x^{T}D^{2}f(z)x\geq 0,\forall x\in \mathbb {R} ^{n}} z ∈ B ( x ⋆ , δ ) {\displaystyle z\in {\mathcal {B}}(x^{\star },\delta )} x ⋆ {\displaystyle x^{\star }}
证明:对于 x ∈ B ( x ⋆ , δ ) {\displaystyle x\in {\mathcal {B}}(x^{\star },\delta )} 令 z = x ⋆ + t ( x − x ⋆ ) ∈ B {\displaystyle z=x^{\star }+t(x-x^{\star })\in {\mathcal {B}}} 根据 泰勒近似 得到: f ( x ) − f ( x ⋆ ) = 0 + 1 2 ( x − x ⋆ ) T D 2 f ( z ) ( x − x ⋆ ) ≥ 0 {\displaystyle f(x)-f(x^{\star })=0+{\frac {1}{2}}(x-x^{\star })^{T}D^{2}f(z)(x-x^{\star })\geq 0} 其中 B ( x ⋆ , δ ) {\displaystyle {\mathcal {B}}(x^{\star },\delta )} 表示以 x ⋆ {\displaystyle x^{\star }} 为中心的开球,即 B ( x ⋆ , δ ) = { x : | | x − x ⋆ | | ≤ δ } {\displaystyle {\mathcal {B}}(x^{\star },\delta )=\{x:||x-x^{\star }||\leq \delta \}} 对于 δ > 0 {\displaystyle \delta >0}
f ( x ) = x 3 {\displaystyle f(x)=x^{3}} D f ( x ⋆ = 0 ) = 0 {\displaystyle Df(x^{\star }=0)=0} x T D 2 f ( z ) x = 6 z x 2 ≱ 0 ( e . g . z = − δ 2 ) {\displaystyle x^{T}D^{2}f(z)x=6zx^{2}\not \geq 0\quad (e.g.\,\,z=-{\frac {\delta }{2}})}
以及
f ( x ) = x 4 {\displaystyle f(x)=x^{4}} D f ( x ⋆ = 0 ) = 0 {\displaystyle Df(x^{\star }=0)=0} x T D 2 f ( z ) x = 12 z 2 x 2 ≥ 0 ∀ z {\displaystyle x^{T}D^{2}f(z)x=12z^{2}x^{2}\geq 0\quad \forall z}
牢记这个小注意事项,我们现在可以转向数值优化程序。
以下所有算法都依赖于以下假设
(A1) 集合 N ( f , f ( x ( 0 ) ) = { x ∈ R n | f ( x ) ≤ f ( x ( 0 ) ) } {\displaystyle N(f,f(x^{(0)})=\{x\in \mathbb {R} ^{n}|f(x)\leq f(x^{(0)})\}} 紧致 的。
其中 x ( 0 ) {\displaystyle x^{(0)}} 魏尔斯特拉斯定理 中,该定理指出每个紧致集都包含其 上确界 下确界 (A1) 保证了 N ( f , f ( x ( 0 ) ) {\displaystyle N(f,f(x^{(0)})} x ⋆ {\displaystyle x^{\star }} D ( f ( x ⋆ ) ) = 0 {\displaystyle D(f(x^{\star }))=0} D ( f ( x ⋆ ) ) = 0 {\displaystyle D(f(x^{\star }))=0}
当然,这种方法的问题是, D ( f ( x ⋆ ) ) = 0 {\displaystyle D(f(x^{\star }))=0} 极大值和鞍点 。因此,好的算法应该确保将极大值和鞍点排除为潜在解。通过要求 f ( x ( k + 1 ) ) < f ( x ( k ) ) {\displaystyle f(x^{(k+1)})<f(x^{(k)})} 序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} x ( k + 1 ) = φ ( x ( k ) ) {\displaystyle x^{(k+1)}=\varphi (x^{(k)})} x ( k ) {\displaystyle x^{(k)}} x ( k + 1 ) {\displaystyle x^{(k+1)}}
方向 d ( k ) {\displaystyle d^{(k)}} 步长 σ ( k ) {\displaystyle \sigma ^{(k)}} 因此,我们可以选择要移动的方向以到达 x ( k + 1 ) {\displaystyle x^{(k+1)}} 以及 此移动的距离。 因此,如果我们选择 d ( k ) {\displaystyle d^{(k)}} σ ( k ) {\displaystyle \sigma ^{(k)}}
引理:如果 d ( k ) ∈ R n {\displaystyle d^{(k)}\in \mathbb {R} ^{n}} D f ( x ) T d ( k ) < 0 {\displaystyle Df(x)^{T}d^{(k)}<0} ∃ σ ¯ > 0 {\displaystyle \exists {\bar {\sigma }}>0}
f ( x + σ ( k ) d ( k ) ) < f ( x ) ∀ σ ∈ ( 0 , σ ¯ ) {\displaystyle f(x+\sigma ^{(k)}d^{(k)})<f(x)\quad \forall \sigma \in (0,{\bar {\sigma }})}
证明:由于 D f ( x ) T d ( k ) < 0 {\displaystyle Df(x)^{T}d^{(k)}<0} D f ( x ) T d ( k ) = lim σ → 0 f ( x + σ ( k ) d ( k ) ) − f ( x ) σ ( k ) {\displaystyle Df(x)^{T}d^{(k)}=\lim _{\sigma \rightarrow 0}{\frac {f(x+\sigma ^{(k)}d^{(k)})-f(x)}{\sigma ^{(k)}}}} σ ( k ) {\displaystyle \sigma ^{(k)}} f ( x + σ ( k ) d ( k ) ) < f ( x ) {\displaystyle f(x+\sigma ^{(k)}d^{(k)})<f(x)}
满足此条件的方向向量 d ( k ) {\displaystyle d^{(k)}} 下降方向 。 在实践中,这个引理允许我们使用以下步骤来数值求解优化问题。
1. 定义序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} x ( k + 1 ) = x ( k ) + σ ( k ) d ( k ) {\displaystyle x^{(k+1)}=x^{(k)}+\sigma ^{(k)}d^{(k)}}
2. 从点 x ( k ) {\displaystyle x^{(k)}} d ( k ) {\displaystyle d^{(k)}}
3. 选择一个步长 σ ( k ) {\displaystyle \sigma ^{(k)}}
4. 如果 | f ( x ( k + 1 ) ) − f ( x ( k ) ) | < ϵ {\displaystyle |f(x^{(k+1)})-f(x^{(k)})|<\epsilon } ϵ > 0 {\displaystyle \epsilon >0}
此过程已经暗示了 d ( k ) {\displaystyle d^{(k)}} σ ( k ) {\displaystyle \sigma ^{(k)}} d ( k ) {\displaystyle d^{(k)}} σ ( k ) {\displaystyle \sigma ^{(k)}} 引理 1 选择的),也不能保证收敛到最小值。乍一看,这似乎有点令人费解。如果我们找到了一个序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} k 趋于无穷大的极限中,我们应该得到解。为什么事实并非如此,可以从以下借鉴自 W. Alt (2002, p. 76) 的例子中看出。
考虑以下例子,它虽然明显是下降的,但并不收敛。设判据函数由以下给出 f ( x ) = x 2 {\displaystyle f(x)=x^{2}} x ( 0 ) = 1 {\displaystyle x^{(0)}=1} d ( k ) = − 1 {\displaystyle d^{(k)}=-1} σ ( k ) = ( 1 2 ) k + 2 {\displaystyle \sigma ^{(k)}=({\frac {1}{2}})^{k+2}} 序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}}
( 2 ) x ( k + 1 ) = x ( k ) + ( 1 2 ) k + 2 ( − 1 ) = x ( k − 1 ) − ( 1 2 ) k + 1 − ( 1 2 ) k + 2 = x ( 0 ) − ∑ j = 0 k ( 1 2 ) j + 2 . {\displaystyle (2)\quad x^{(k+1)}=x^{(k)}+({\frac {1}{2}})^{k+2}(-1)=x^{(k-1)}-\left({\frac {1}{2}}\right)^{k+1}-\left({\frac {1}{2}}\right)^{k+2}=x^{(0)}-\sum _{j=0}^{k}\left({\frac {1}{2}}\right)^{j+2}.}
注意, x ( k ) > 0 ∀ k {\displaystyle x^{(k)}>0\,\,\forall \,\,k} f ( x ( k + 1 ) ) < f ( x ( k ) ) ∀ k {\displaystyle f(x^{(k+1)})<f(x^{(k)})\,\,\forall \,\,k}
( 3 ) lim k → ∞ x ( k ) = lim k → ∞ x ( 0 ) − ∑ j = 0 k − 1 ( 1 2 ) j + 2 = lim k → ∞ 1 − 1 4 ( 1 − ( 1 2 ) k 1 2 ) = lim k → ∞ 1 2 + ( 1 2 ) k + 1 = 1 2 ≠ 0 = x ⋆ . {\displaystyle (3)\quad \lim _{k\rightarrow \infty }x^{(k)}=\lim _{k\rightarrow \infty }x^{(0)}-\sum _{j=0}^{k-1}\left({\frac {1}{2}}\right)^{j+2}=\lim _{k\rightarrow \infty }1-{\frac {1}{4}}\left({\frac {1-\left({\frac {1}{2}}\right)^{k}}{\frac {1}{2}}}\right)=\lim _{k\rightarrow \infty }{\frac {1}{2}}+\left({\frac {1}{2}}\right)^{k+1}={\frac {1}{2}}\neq 0=x^{\star }.}
这种不收敛的原因必须归因于步长 σ ( k ) {\displaystyle \sigma ^{(k)}} k ,步长 x ( k + 1 ) − x ( k ) {\displaystyle x^{(k+1)}-x^{(k)}} d ( k ) {\displaystyle d^{(k)}}
这种联系的明显思路是要求实际下降与一阶近似成正比,即选择 σ ( k ) {\displaystyle \sigma ^{(k)}} c 1 > 0 {\displaystyle c_{1}>0}
( 4 ) f ( x ( k ) + σ ( k ) d ( k ) ) − f ( x ( k ) ) ≤ c 1 σ ( k ) D ( f ( x ( k ) ) ) d ( k ) < 0. {\displaystyle (4)\quad f(x^{(k)}+\sigma ^{(k)}d^{(k)})-f(x^{(k)})\leq c_{1}\sigma ^{(k)}D(f(x^{(k)}))d^{(k)}<0.}
注意,我们仍然只关注下降方向,因此 D f ( x ( k ) ) T d ( k ) < 0 {\displaystyle Df(x^{(k)})^{T}d^{(k)}<0} N ( f , f ( x ( k ) ) ) {\displaystyle N(f,f(x^{(k)}))} 收敛 ,并且根据 (4)
( 5 ) lim k → ∞ σ ( k ) D ( f ( x ( k ) ) ) d ( k ) = 0. {\displaystyle (5)\quad \lim _{k\rightarrow \infty }\sigma ^{(k)}D(f(x^{(k)}))d^{(k)}=0.}
最后,我们希望选择一个序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} lim k → ∞ D ( f ( x ( k ) ) ) = 0 {\displaystyle \lim _{k\rightarrow \infty }D(f(x^{(k)}))=0} lim k → ∞ D ( f ( x ( k ) ) ) = 0 {\displaystyle \lim _{k\rightarrow \infty }D(f(x^{(k)}))=0} σ ( k ) {\displaystyle \sigma ^{(k)}}
( 6 ) σ ( k ) ≥ − c 2 D f ( x ( k ) ) T d ( k ) | | d ( k ) | | 2 > 0 {\displaystyle (6)\quad \sigma ^{(k)}\geq -c_{2}{\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||^{2}}}>0}
对于某个常数 c 2 > 0 {\displaystyle c_{2}>0}
( 7 ) f ( x ( k ) + σ ( k ) d ( k ) ) − f ( x ( k ) ) ≤ − c ( D f ( x ( k ) ) T d ( k ) | | d ( k ) | | ) 2 , c = c 1 c 2 {\displaystyle (7)\quad f(x^{(k)}+\sigma ^{(k)}d^{(k)})-f(x^{(k)})\leq -c\left({\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||}}\right)^{2},\quad c=c_{1}c_{2}}
其中,紧致性 N ( f , f ( x ( k ) ) ) {\displaystyle N(f,f(x^{(k)}))} 收敛 ,因此
( 8 ) lim k → ∞ − c ( D f ( x ( k ) ) T d ( k ) | | d ( k ) | | ) 2 = lim k → ∞ D f ( x ( k ) ) T d ( k ) | | d ( k ) | | = 0 {\displaystyle (8)\quad \lim _{k\rightarrow \infty }-c({\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||}})^{2}=\lim _{k\rightarrow \infty }{\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||}}=0}
满足 (4) 和 (6) 的步长被称为有效步长 ,并用 σ E ( k ) {\displaystyle \sigma _{E}^{(k)}}
需要注意的是,正是 (6) 的失败导致示例 1 未能收敛。将示例中的步长代入 (6) 中得到 ( 6.1 ) σ ( k ) = ( 1 2 ) ( k + 2 ) ≥ − c 2 2 x ( k ) ( − 1 ) 1 = c 2 ⋅ 2 ( 1 2 + ( 1 2 ) k + 1 ) ⇔ 1 4 ( 1 + 2 ( k ) ) ≥ c 2 > 0 {\displaystyle (6.1)\quad \sigma ^{(k)}=\left({\frac {1}{2}}\right)^{(k+2)}\geq -c_{2}{\frac {2x^{(k)}(-1)}{1}}=c_{2}\cdot 2({\frac {1}{2}}+\left({\frac {1}{2}})^{k+1}\right)\Leftrightarrow {\frac {1}{4(1+2^{(k)})}}\geq c_{2}>0}
因此,对于所有k ,没有 常数 c 2 > 0 {\displaystyle c_{2}>0} σ ( k ) = ( 1 2 ) k + 1 {\displaystyle \sigma ^{(k)}=\left({\frac {1}{2}}\right)^{k+1}}
( 6.2 ) lim k → ∞ x ( k + 1 ) = lim k → ∞ x ( 0 ) − 1 2 ∑ i ( 1 2 ) i = lim k → ∞ ( 1 2 ) k + 1 = 0 = x ⋆ , {\displaystyle (6.2)\quad \lim _{k\rightarrow \infty }x^{(k+1)}=\lim _{k\rightarrow \infty }x^{(0)}-{\frac {1}{2}}\sum _{i}\left({\frac {1}{2}}\right)^{i}=\lim _{k\rightarrow \infty }\left({\frac {1}{2}}\right)^{k+1}=0=x^{\star },}
也就是说,收敛 确实发生了。此外,认识到这个例子实际上确实满足条件 (6),因为
( 6.3 ) σ ( k ) = ( 1 2 ) ( k + 1 ) ≥ − c 2 2 x ( k ) ( − 1 ) 1 = c 2 ⋅ 2 ( 1 2 ) k ⇔ 1 4 ≥ c 2 > 0. {\displaystyle (6.3)\quad \sigma ^{(k)}=\left({\frac {1}{2}}\right)^{(k+1)}\geq -c_{2}{\frac {2x^{(k)}(-1)}{1}}=c_{2}\cdot 2\left({\frac {1}{2}}\right)^{k}\Leftrightarrow {\frac {1}{4}}\geq c_{2}>0.}
我们已经论证过,选择 σ ( k ) {\displaystyle \sigma ^{(k)}} d ( k ) {\displaystyle d^{(k)}} d ( k ) {\displaystyle d^{(k)}} σ ( k ) {\displaystyle \sigma ^{(k)}} 有效的步长 意味着
( 8 ′ ) lim k → ∞ − c ( D f ( x ( k ) ) T d ( k ) | | d ( k ) | | ) 2 = lim k → ∞ D f ( x ( k ) ) T d ( k ) | | d ( k ) | | = 0. {\displaystyle (8')\quad \lim _{k\rightarrow \infty }-c({\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||}})^{2}=\lim _{k\rightarrow \infty }{\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||}}=0.}
因此,“正确”的方向向量将保证 (8') 意味着
( 9 ) lim k → ∞ D f ( x ( k ) ) = 0 {\displaystyle (9)\quad \lim _{k\rightarrow \infty }Df(x^{(k)})=0}
因为 (9) 是选择序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} σ k {\displaystyle \sigma _{k}} 有效 的,并且定义
( 10 ) β ( k ) = D f ( x ( k ) ) T d ( k ) | | D f ( x ( k ) ) | | | | d ( k ) | | ⇔ β ( k ) | | D f ( x ( k ) ) | | = D f ( x ( k ) ) T d ( k ) | | d ( k ) | | {\displaystyle (10)\quad \beta ^{(k)}={\frac {Df(x^{(k)})^{T}d^{(k)}}{||Df(x^{(k)})||||d^{(k)}||}}\quad \Leftrightarrow \quad \beta ^{(k)}||Df(x^{(k)})||={\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||}}}
根据 (8') 和 (10) 我们知道
( 11 ) lim k → ∞ β ( k ) | | D f ( x ( k ) ) | | = 0. {\displaystyle (11)\quad \lim _{k\rightarrow \infty }\beta ^{(k)}||Df(x^{(k)})||=0.}
所以如果我们从下方对 β ( k ) {\displaystyle \beta ^{(k)}} β ( k ) ≤ − δ < 0 {\displaystyle \beta ^{(k)}\leq -\delta <0}
( 12 ) lim k → ∞ β ( k ) | | D f ( x ( k ) ) | | = lim k → ∞ | | D f ( x ( k ) ) | | = lim k → ∞ D f ( x ( k ) ) = 0 , {\displaystyle (12)\quad \lim _{k\rightarrow \infty }\beta ^{(k)}||Df(x^{(k)})||=\lim _{k\rightarrow \infty }||Df(x^{(k)})||=\lim _{k\rightarrow \infty }Df(x^{(k)})=0,}
其中,(12) 只给出了序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} x ⋆ {\displaystyle x^{\star }} β ( k ) {\displaystyle \beta ^{(k)}} d ( k ) {\displaystyle d^{(k)}} β ( k ) {\displaystyle \beta ^{(k)}} d ( k ) {\displaystyle d^{(k)}}
当考虑对 β ( k ) {\displaystyle \beta ^{(k)}}
β k = D ( f ( x ) ) d ( k ) | | D f ( x ( k ) ) | | | | d ( k ) | | = cos ( D f ( x ( k ) ) , d ( k ) ) {\displaystyle \beta _{k}={\frac {D(f(x))d^{(k)}}{||Df(x^{(k)})||||d^{(k)}||}}=\cos(Df(x^{(k)}),d^{(k)})}
给出的 β ( k ) {\displaystyle \beta ^{(k)}}
假设 σ ( k ) {\displaystyle \sigma ^{(k)}} 已经被有效地选择,并且 d ( k ) {\displaystyle d^{(k)}} 满足
( 13 ) cos ( D f ( x ( k ) ) , d ( k ) ) = β k ≤ − δ < 0 {\displaystyle (13)\quad \cos(Df(x^{(k)}),d^{(k)})=\beta _{k}\leq -\delta <0}
我们有
( 14 ) lim k → ∞ D f ( x ( k ) ) → 0 {\displaystyle (14)\quad \lim _{k\rightarrow \infty }Df(x^{(k)})\rightarrow 0}
因此:如果 x ( k ) {\displaystyle x^{(k)}} 处的负梯度与方向 d ( k ) {\displaystyle d^{(k)}} 之间的夹角始终小于直角,那么就会发生收敛。依赖于满足 (13) 的 d ( k ) {\displaystyle d^{(k)}} 的方法被称为梯度方法。
换句话说:只要不沿梯度的正交 方向移动,并且有效地选择步长,梯度方法 就能保证收敛到解 x ⋆ {\displaystyle x^{\star }}
现在让我们探索这类别中三种具体的算法,它们在各自的 d ( k ) {\displaystyle d^{(k)}}
牛顿法 根 的著名方法,因此可以轻松地应用于优化问题。牛顿法的主要思想是将方程组线性化,得到
( 15 ) g ( x ) = g ( x ^ ) + D g ( x ^ ) T ( x − x ^ ) = 0. {\displaystyle (15)\quad g(x)=g({\hat {x}})+Dg({\hat {x}})^{T}(x-{\hat {x}})=0.}
(15) 可以很容易地解出 x ,因为解仅由(假设 D g ( x ^ ) T {\displaystyle Dg({\hat {x}})^{T}} 非奇异 )给出
( 16 ) x = x ^ − [ D g ( x ^ ) T ] − 1 g ( x ^ ) . {\displaystyle (16)\quad x={\hat {x}}-[Dg({\hat {x}})^{T}]^{-1}g({\hat {x}}).}
为了我们的目的,我们只选择 g ( x ) {\displaystyle g(x)} D f ( x ) {\displaystyle Df(x)}
( 17 ) d N ( k ) = x ( k + 1 ) − x ( k ) = − [ D 2 f ( x ( k ) ) ] − 1 D f ( x ( k ) ) {\displaystyle (17)\quad d_{N}^{(k)}=x^{(k+1)}-x^{(k)}=-[D^{2}f(x^{(k)})]^{-1}Df(x^{(k)})}
其中 d N ( k ) {\displaystyle d_{N}^{(k)}}
分析 (17) 可以揭示牛顿法的主要性质
如果 D 2 f ( x ( k ) ) {\displaystyle D^{2}f(x^{(k)})} 正定矩阵 ,那么 d N k {\displaystyle d_{N}^{k}} 牛顿法使用一阶 *和* 二阶导数的局部信息来计算 d N k {\displaystyle d_{N}^{k}} ( 18 ) x ( k + 1 ) = x ( k ) + d N ( k ) {\displaystyle (18)\quad x^{(k+1)}=x^{(k)}+d_{N}^{(k)}}
牛顿法使用固定步长 σ ( k ) = 1 {\displaystyle \sigma ^{(k)}=1} σ ( k ) = 1 {\displaystyle \sigma ^{(k)}=1} σ k ¯ {\displaystyle {\bar {\sigma _{k}}}}
该方法可能非常耗时,因为每一步 *k* 都要计算 [ D 2 f ( x ( k ) ) ] − 1 {\displaystyle [D^{2}f(x^{(k)})]^{-1}} 为了确保该方法是下降法,我们可以使用一个有效的步长 σ E ( k ) {\displaystyle \sigma _{E}^{(k)}} ( 19 ) x ( k + 1 ) = x ( k ) − σ E ( k ) d N ( k ) = x ( k ) − σ E ( k ) [ D 2 f ( x k ) ] − 1 D f ( x ( k ) ) {\displaystyle (19)\quad x^{(k+1)}=x^{(k)}-\sigma _{E}^{(k)}d_{N}^{(k)}=x^{(k)}-\sigma _{E}^{(k)}[D^{2}f(x^{k})]^{-1}Df(x^{(k)})}
另一个常用的方法是最速下降法 d ( k ) {\displaystyle d^{(k)}} f 的下降最大。虽然乍一看这个过程似乎很有道理,但它实际上利用的信息比牛顿法 少,因为它忽略了Hessian关于函数曲率的信息。尤其是在下面的应用中,我们将看到一些关于这个问题的例子。
最速下降法 的方向向量由下式给出:
( 20 ) d S D ( k ) = a r g m a x d : | | d | | = r { − D f ( x ( k ) ) T d } = a r g m i n d : | | d | | = r { D f ( x ( k ) ) T d } = − r D f ( x ) | | D f ( x ) | | {\displaystyle (20)\quad d_{SD}^{(k)}=argmax_{d:||d||=r}\{-Df(x^{(k)})^{T}d\}=argmin_{d:||d||=r}\{Df(x^{(k)})^{T}d\}=-r{\frac {Df(x)}{||Df(x)||}}}
证明:根据柯西-施瓦茨不等式 ,可得
( 21 ) D f ( x ) T d | | D f ( x ) | | | | d | | ≥ − 1 ⇔ D f ( x ) T d ≥ − r | | D f ( x ) | | . {\displaystyle (21)\quad {\frac {Df(x)^{T}d}{||Df(x)||||d||}}\geq -1\quad \Leftrightarrow \quad Df(x)^{T}d\geq -r||Df(x)||.}
显然 (21) 等式对 d ( k ) = d S D ( k ) {\displaystyle d^{(k)}=d_{SD}^{(k)}} 在 (20) 中给出。
特别要注意,对于 r = | | D f ( x ) | | {\displaystyle r=||Df(x)||} d S D ( k ) = − D f ( x ( k ) ) {\displaystyle d_{SD}^{(k)}=-Df(x^{(k)})} σ E ( k ) {\displaystyle \sigma _{E}^{(k)}} { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}}
( 22 ) x ( k + 1 ) = x ( k ) + σ E ( k ) d S D ( k ) , {\displaystyle (22)\quad x^{(k+1)}=x^{(k)}+\sigma _{E}^{(k)}d_{SD}^{(k)},}
其中 σ E ( k ) {\displaystyle \sigma _{E}^{(k)}} d S D ( k ) {\displaystyle d_{SD}^{(k)}}
对于 d S D ( k ) = − r D f ( x ) | | D f ( x ) | | {\displaystyle d_{SD}^{(k)}=-r{\frac {Df(x)}{||Df(x)||}}} D f ( x ) T d S D ( k ) = D f ( x ) T ( − r D f ( x ) | | D f ( x ) | | ) = − r | | D f ( x ) | | D f ( x ) T D f ( x ) < 0. {\displaystyle Df(x)^{T}d_{SD}^{(k)}=Df(x)^{T}\left(-r{\frac {Df(x)}{||Df(x)||}}\right)=-{\frac {r}{||Df(x)||}}Df(x)^{T}Df(x)<0.}
*最速下降法* 只是局部上可行的,因为它忽略了二阶信息。 特别是当目标函数很平坦时(即解 x ⋆ {\displaystyle x^{\star }} 由于它不需要 Hessian 矩阵,因此 *最速下降法* 的计算和实现很简单快捷。 比 *牛顿法* 和 *最速下降法* 更通用的方法是 *可变度量法* 类。这类方法依赖于更新公式
( 23 ) x k + 1 = x k − σ E ( k ) [ A k ] − 1 D f ( x k ) . {\displaystyle (23)\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}[A^{k}]^{-1}Df(x^{k}).}
如果 A k {\displaystyle A^{k}} 对称 且 正定 矩阵,(23) 定义了一个下降方法,其中 [ A k ] − 1 {\displaystyle [A^{k}]^{-1}} A k {\displaystyle A^{k}} 谱分解
( 24 ) A k = Γ Λ Γ T {\displaystyle (24)\quad A^{k}=\Gamma \Lambda \Gamma ^{T}}
其中 Γ {\displaystyle \Gamma } Λ {\displaystyle \Lambda } 特征向量 和 特征值 的矩阵。如果 A k {\displaystyle A^{k}} λ i {\displaystyle \lambda _{i}} λ i − 1 {\displaystyle \lambda _{i}^{-1}} [ A k ] − 1 = Γ Λ − 1 Γ T {\displaystyle [A^{k}]^{-1}=\Gamma \Lambda ^{-1}\Gamma ^{T}} d ( k ) = [ A k ] − 1 D f ( x k ) {\displaystyle d^{(k)}=[A^{k}]^{-1}Df(x^{k})}
( 25 ) D f ( x k ) T d ( k ) = − D f ( x k ) T [ A k ] − 1 D f ( x k ) ≡ − v T [ A k ] − 1 v ≤ 0 , {\displaystyle (25)\quad Df(x^{k})^{T}d^{(k)}=-Df(x^{k})^{T}[A^{k}]^{-1}Df(x^{k})\equiv -v^{T}[A^{k}]^{-1}v\leq 0,}
也就是说,该方法确实是下降的。到目前为止,我们还没有指定矩阵 A k {\displaystyle A^{k}} 可变度量法 恰好与最速下降法 和牛顿法 重合。
对于 A k = I {\displaystyle A^{k}={\mathcal {I}}} I {\displaystyle {\mathcal {I}}} 单位矩阵 ),可以得出 ( 22 ′ ) x k + 1 = x k − σ E ( k ) D f ( x k ) {\displaystyle (22')\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}Df(x^{k})}
这仅仅是*最速下降法*。
对于 A k = D 2 f ( x k ) {\displaystyle A^{k}=D^{2}f(x^{k})} ( 19 ′ ) x k + 1 = x k − σ E ( k ) [ D 2 f ( x k ) ] − 1 D f ( x k ) {\displaystyle (19')\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}[D^{2}f(x^{k})]^{-1}Df(x^{k})}
这仅仅是使用步长 σ E ( k ) {\displaystyle \sigma _{E}^{(k)}}
对于*变量度量法*,另一个自然候选者是*拟牛顿法*。与标准*牛顿法*相比,它使用有效的步长,使其成为下降法;与*最速下降法*相比,它不会完全忽略函数曲率的局部信息。因此,*拟牛顿法*由矩阵 A k {\displaystyle A^{k}}
A k {\displaystyle A^{k}} D 2 f ( x k ) {\displaystyle D^{2}f(x^{k})} 更新 A k → A k + 1 {\displaystyle A^{k}\rightarrow A^{k+1}} 为了确保第一个要求, A k + 1 {\displaystyle A^{k+1}}
( 26 ) A k + 1 ( x ( k + 1 ) − x ( k ) ) = D f ( x ( k + 1 ) ) − D f ( x ( k ) ) {\displaystyle (26)\quad A^{k+1}(x^{(k+1)}-x^{(k)})=Df(x^{(k+1)})-Df(x^{(k)})}
因为所有满足 (26) 的 A k {\displaystyle A^{k}}
( 27 ) g ( x ) = f ( x k + 1 ) + D f ( x k + 1 ) T ( x − x k + 1 ) + 1 2 ( x − x k + 1 ) T A k + 1 ( x − x k + 1 ) . {\displaystyle (27)\quad g(x)=f(x^{k+1})+Df(x^{k+1})^{T}(x-x^{k+1})+{\frac {1}{2}}(x-x^{k+1})^{T}A^{k+1}(x-x^{k+1}).}
显然, g ( x k + 1 ) = f ( x k + 1 ) {\displaystyle g(x^{k+1})=f(x^{k+1})} D g ( x k + 1 ) = D f ( x k + 1 ) {\displaystyle Dg(x^{k+1})=Df(x^{k+1})} g ( x ) {\displaystyle g(x)} f ( x ) {\displaystyle f(x)} x ( k + 1 ) {\displaystyle x^{(k+1)}} g ( x ) {\displaystyle g(x)} x ( k ) {\displaystyle x^{(k)}} A k + 1 {\displaystyle A^{k+1}} x ( k ) {\displaystyle x^{(k)}}
( 28 ) D g ( x k ) = D f ( x k + 1 ) − A k + 1 ( x k + 1 − x k ) {\displaystyle (28)\quad Dg(x^{k})=Df(x^{k+1})-A^{k+1}(x^{k+1}-x^{k})}
很明显,如果 A k + 1 {\displaystyle A^{k+1}} 拟牛顿方程 ,则 D g ( x k ) = D f ( x k ) {\displaystyle Dg(x^{k})=Df(x^{k})}
( 29 ) A k + 1 ( x k + 1 − x k ) = D f ( x k + 1 ) − D g ( x k ) = D f ( x k + 1 ) − D f ( x k ) = D 2 f ( λ x ( k ) + ( 1 − λ ) x ( k + 1 ) ) ( x k + 1 − x k ) . {\displaystyle (29)\quad A^{k+1}(x^{k+1}-x^{k})=Df(x^{k+1})-Dg(x^{k})=Df(x^{k+1})-Df(x^{k})=D^{2}f(\lambda x^{(k)}+(1-\lambda )x^{(k+1)})(x^{k+1}-x^{k}).}
因此,只要 x ( k + 1 ) {\displaystyle x^{(k+1)}} x ( k ) {\displaystyle x^{(k)}} A k + 1 {\displaystyle A^{k+1}} D 2 f ( x ( k ) ) {\displaystyle D^{2}f(x^{(k)})}
现在让我们来谈谈第二个要求,即 A k {\displaystyle A^{k}} BFGS 算法 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} { D f ( x ( k ) ) } k {\displaystyle \{Df(x^{(k)})\}_{k}} A ( k + 1 ) {\displaystyle A^{(k+1)}} x ( 0 ) {\displaystyle x^{(0)}}
( 30 ) A k = A k − 1 − ( A k − 1 ) T γ k − 1 T γ k − 1 A k − 1 γ k − 1 T A k − 1 γ k − 1 + Δ k − 1 Δ k − 1 T Δ k − 1 T γ k − 1 {\displaystyle (30)\quad A^{k}=A^{k-1}-{\frac {(A^{k-1})^{T}\gamma _{k-1}^{T}\gamma _{k-1}A^{k-1}}{\gamma _{k-1}^{T}A^{k-1}\gamma _{k-1}}}+{\frac {\Delta _{k-1}\Delta _{k-1}^{T}}{\Delta _{k-1}^{T}\gamma _{k-1}}}}
其中 Δ k − 1 = D f ( x ( k ) ) − D f ( x ( k − 1 ) ) {\displaystyle \Delta _{k-1}=Df(x^{(k)})-Df(x^{(k-1)})} γ k − 1 = x ( k ) − x ( k − 1 ) {\displaystyle \gamma _{k-1}=x^{(k)}-x^{(k-1)}} A k {\displaystyle A^{k}}
它利用了关于 f ( x ) {\displaystyle f(x)} A k {\displaystyle A^{k}} D 2 f ( x ) {\displaystyle D^{2}f(x)} 尽管如此,它确保了简单快速的更新(例如,通过 BFGS 算法),因此它比标准牛顿法更快。 它是一种下降方法,因为 A k {\displaystyle A^{k}} 它相对容易实现,因为 BFGS 算法在大多数数值或统计软件包中都可用。 为了比较这些方法并说明算法之间的差异,我们现在将评估 *最速下降法*、标准 *牛顿法* 和使用高效步长的 *拟牛顿法* 的性能。我们在这个领域使用两个经典函数,即 Himmelblau 函数和 Rosenbrock 函数。
Himmelblau 函数定义为
( 31 ) f ( x , y ) = ( x 2 + y − 11 ) 2 + ( x + y 2 − 7 ) 2 {\displaystyle (31)\quad f(x,y)=(x^{2}+y-11)^{2}+(x+y^{2}-7)^{2}}
这个四阶多项式有四个极小值、四个鞍点和一个极大值,因此算法有足够多的可能性失败。在下图中,我们展示了不同起始值的函数的 *等高线图* 和 3D 图。
在图 1 中,我们展示了函数以及三种方法在起始值为 ( 2 , − 4 ) {\displaystyle (2,-4)}
图 1:两种牛顿法收敛到同一个极小值,而最速下降法收敛到另一个极小值。 现在考虑起始值为 ( 4.5 , − 0.5 ) {\displaystyle (4.5,-0.5)} σ {\displaystyle \sigma }
图 2:即使所有方法都找到了不同的解。 Rosenbrock 函数定义为
( 32 ) f ( x , y ) = 100 ( y − x 2 ) 2 + ( 1 − x ) 2 {\displaystyle (32)\quad f(x,y)=100(y-x^{2})^{2}+(1-x)^{2}\ }
尽管该函数只有一个最小值,但对于优化问题而言,它仍然是一个有趣的函数。原因是该U形函数的谷底非常平坦(参见图3和图4的右侧面板)。对于计量经济学家而言,这个函数可能非常有趣,因为在最大似然估计的情况下,平坦的准则函数非常常见。因此,下面图3和图4中显示的结果对于具有该问题的函数来说似乎是比较通用的。
我在使用这个函数和算法时的经验是,图3(给定一个初始值 ( 2 , − 5 ) {\displaystyle (2,-5)}
图3:所有方法都找到了相同的解,但最速下降法波动很大。 图4考虑的是一个初始值 ( − 2 , − 2 ) {\displaystyle (-2,-2)} [ D f ( x ( k ) ) ] − 1 D f ( x ( k ) ) ) {\displaystyle [Df(x^{(k)})]^{-1}Df(x^{(k)}))}
图2:由于固定步长导致的牛顿法过冲。 对于计量经济学家和统计学家来说,*最大似然估计器*可能是数值优化算法最重要的应用。因此,我们将简要介绍估计过程如何融入上面开发的框架。
像往常一样,设
( 33 ) f ( Y | X ; θ ) {\displaystyle (33)\quad f(Y|X;\theta )}
为给定 *X* 的 *Y* 的*条件密度*,其中参数为 θ {\displaystyle \theta }
( 34 ) l ( θ ; Y | X ) {\displaystyle (34)\quad l(\theta ;Y|X)}
为参数 θ {\displaystyle \theta }
如果我们假设数据是*独立同分布(iid)*,则样本对数似然函数如下所示:
( 35 ) L ( θ ; Y 1 , … , Y N ) = ∑ i N L ( θ ; Y i ) = ∑ i N log ( l ( θ ; Y i ) ) . {\displaystyle (35)\quad {\mathcal {L}}(\theta ;Y_{1},\dots ,Y_{N})=\sum _{i}^{N}{\mathcal {L}}(\theta ;Y_{i})=\sum _{i}^{N}\log(l(\theta ;Y_{i})).}
因此,最大似然估计归结为关于参数 θ {\displaystyle \theta } { θ ( k ) } k {\displaystyle \{\theta ^{(k)}\}_{k}}
( 36 ) D θ L ( θ ( k + 1 ) ) = D θ L ( θ ( k ) ) + D θ θ L ( θ ( k ) ) ( θ ( k + 1 ) − θ ( k ) ) = 0 ⇔ θ ( k + 1 ) = θ ( k ) − [ D θ θ L ( θ ( k ) ) ] − 1 D θ L ( θ ( k ) ) {\displaystyle (36)\quad D_{\theta }{\mathcal {L}}(\theta ^{(k+1)})=D_{\theta }{\mathcal {L}}(\theta ^{(k)})+D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})(\theta ^{(k+1)}-\theta ^{(k)})=0\Leftrightarrow \theta ^{(k+1)}=\theta ^{(k)}-[D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})]^{-1}D_{\theta }{\mathcal {L}}(\theta ^{(k)})}
D θ L {\displaystyle D_{\theta }{\mathcal {L}}} D θ θ L {\displaystyle D_{\theta \theta }{\mathcal {L}}} θ {\displaystyle \theta } [ D θ θ L ( θ ( k ) ) ] − 1 D θ L ( θ ( k ) ) {\displaystyle [D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})]^{-1}D_{\theta }{\mathcal {L}}(\theta ^{(k)})} θ {\displaystyle \theta }
假设一个简单的线性模型
( 37 a ) Y i = β 1 + β x X i + U i {\displaystyle (37a)\quad Y_{i}=\beta _{1}+\beta _{x}X_{i}+U_{i}}
其中 θ = ( β 1 , β 2 ) ′ {\displaystyle \theta =(\beta _{1},\beta _{2})'} Y 由 U 的分布决定,即
( 37 b ) p ( Y i − β 1 − β x X i ) ≡ p ∣ X i ( Y i ) = p ( U i ) , {\displaystyle (37b)\quad p(Y_{i}-\beta _{1}-\beta _{x}X_{i})\equiv p_{\mid X_{i}}(Y_{i})=p(U_{i}),}
其中 p {\displaystyle p} 密度函数 。一般来说,最大化 (35) 没有闭式解(至少如果 U 碰巧不是正态分布 ),因此必须使用数值方法。因此假设 U 遵循学生 t 分布 ,具有 m 自由度 ,因此 (35) 由下式给出
( 38 ) L ( θ ; Y ∣ X ) = ∑ log ( Γ ( m + 1 2 ) π m Γ ( m 2 ) ( 1 + ( y i − x i T β ) 2 m ) − m + 1 2 ) {\displaystyle (38)\quad {\mathcal {L}}(\theta ;Y_{\mid X})=\sum \log \left({\frac {\Gamma ({\frac {m+1}{2}})}{{\sqrt {\pi m}}\Gamma ({\frac {m}{2}})}}(1+{\frac {(y_{i}-x_{i}^{T}\beta )^{2}}{m}})^{-{\frac {m+1}{2}}}\right)}
这里我们只使用了 t 分布的密度函数的定义。 (38) 可以简化为
( 39 ) L ( θ ; Y ∣ X ) = N [ log ( Γ ( m + 1 2 ) ) − log ( π m Γ ( m 2 ) ) ] − m + 1 2 ∑ log ( 1 + ( y i − x i T β ) 2 m ) {\displaystyle (39)\quad {\mathcal {L}}(\theta ;Y_{\mid X})=N\left[\log \left(\Gamma \left({\frac {m+1}{2}}\right)\right)-\log \left({\sqrt {\pi m}}\Gamma \left({\frac {m}{2}}\right)\right)\right]-{\frac {m+1}{2}}\sum \log \left(1+{\frac {(y_{i}-x_{i}^{T}\beta )^{2}}{m}}\right)}
因此(如果我们假设自由度 m 是已知的)
( 40 ) argmax { L ( θ ; Y ∣ X ) } = argmax { − m + 1 2 ∑ log ( 1 + ( y i − x i T β ) 2 m ) } = argmin { ∑ log ( 1 + ( y i − x i T β ) 2 m ) } . {\displaystyle (40)\quad {\textit {argmax}}\left\{{\mathcal {L}}(\theta ;Y_{\mid X})\right\}={\textit {argmax}}\left\{-{\frac {m+1}{2}}\sum \log \left(1+{\frac {(y_{i}-x_{i}^{T}\beta )^{2}}{m}}\right)\right\}={\textit {argmin}}\left\{\sum \log \left(1+{\frac {(y_{i}-x_{i}^{T}\beta )^{2}}{m}}\right)\right\}.}
使用以下准则函数
( 41 ) f ( β 1 , β 2 ) = ∑ log ( 1 + ( y i − β 1 − β 2 x i ) 2 m ) {\displaystyle (41)\quad f(\beta _{1},\beta _{2})=\sum \log \left(1+{\frac {(y_{i}-\beta _{1}-\beta _{2}x_{i})^{2}}{m}}\right)}
上述方法可以很容易地应用于计算最大似然估计 ( β ^ 1 , M L , β ^ 2 , M L ) {\displaystyle ({\hat {\beta }}_{1,ML},{\hat {\beta }}_{2,ML})}
Alt, W. (2002): "Nichtlineare Optimierung", Vieweg: Braunschweig/Wiesbaden
Härdle, W. 和 Simar, L. (2003): "应用多元统计分析", Springer: Berlin Heidelberg
Königsberger, K. (2004): "分析 I", Springer: Berlin Heidelberg
Ruud, P. (2000): "古典计量经济学理论", 牛津大学出版社: 纽约 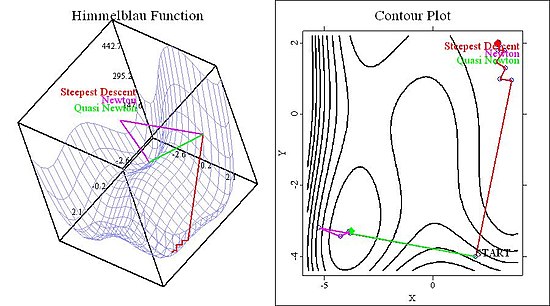




















































































![{\displaystyle (16)\quad x={\hat {x}}-[Dg({\hat {x}})^{T}]^{-1}g({\hat {x}}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/973ad4b1a68c0301124de9a8e4a9f5dcf2ede103)

![{\displaystyle (17)\quad d_{N}^{(k)}=x^{(k+1)}-x^{(k)}=-[D^{2}f(x^{(k)})]^{-1}Df(x^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78f590fdfab4360315b24683a209d394d474d8d5)






![{\displaystyle [D^{2}f(x^{(k)})]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18f24df6687d0360e41c29464f4aaf177e9314f9)
![{\displaystyle (19)\quad x^{(k+1)}=x^{(k)}-\sigma _{E}^{(k)}d_{N}^{(k)}=x^{(k)}-\sigma _{E}^{(k)}[D^{2}f(x^{k})]^{-1}Df(x^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e7b82c56b6571dc71773a1301041f3e514bb0be)









![{\displaystyle (23)\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}[A^{k}]^{-1}Df(x^{k}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8b5580a0328e0fc4cb23c05d2aaa2dfb757e774)

![{\displaystyle [A^{k}]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6caa38bd6a32cf081b1e8379b42ccafdeaf56056)





![{\displaystyle [A^{k}]^{-1}=\Gamma \Lambda ^{-1}\Gamma ^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0bb61f96e4008fe7ac42ddae42174a1cbc74f22)
![{\displaystyle d^{(k)}=[A^{k}]^{-1}Df(x^{k})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2dd88606c2704c7ca9ba41fbff98dc6196d731f1)
![{\displaystyle (25)\quad Df(x^{k})^{T}d^{(k)}=-Df(x^{k})^{T}[A^{k}]^{-1}Df(x^{k})\equiv -v^{T}[A^{k}]^{-1}v\leq 0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19c3cfc50845559d027b7a787662c23b8209bdba)




![{\displaystyle (19')\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}[D^{2}f(x^{k})]^{-1}Df(x^{k})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e585e07182f56dfbe1ebb268e5b1feba19cac6e)























![{\displaystyle [Df(x^{(k)})]^{-1}Df(x^{(k)}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60231e722c13de70156e005a9956e01b4895cda1)





![{\displaystyle (36)\quad D_{\theta }{\mathcal {L}}(\theta ^{(k+1)})=D_{\theta }{\mathcal {L}}(\theta ^{(k)})+D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})(\theta ^{(k+1)}-\theta ^{(k)})=0\Leftrightarrow \theta ^{(k+1)}=\theta ^{(k)}-[D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})]^{-1}D_{\theta }{\mathcal {L}}(\theta ^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27be895a860dcd9530a4d300fdc8fa7f7e7f9e3c)


![{\displaystyle [D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})]^{-1}D_{\theta }{\mathcal {L}}(\theta ^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1bb702f696e4c7c16d636cdafdbf51382f32bfd)





![{\displaystyle (39)\quad {\mathcal {L}}(\theta ;Y_{\mid X})=N\left[\log \left(\Gamma \left({\frac {m+1}{2}}\right)\right)-\log \left({\sqrt {\pi m}}\Gamma \left({\frac {m}{2}}\right)\right)\right]-{\frac {m+1}{2}}\sum \log \left(1+{\frac {(y_{i}-x_{i}^{T}\beta )^{2}}{m}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56ab57a856625145f8bd9be4f656dba107baf35a)


