材料力学/未分类主题

相容条件

在工程力学课程中，我们使用力的平衡来求解各个构件中的力。但是，在某些情况下，这是不可能的，这些问题被认为是静不定问题。它们需要一些本构方程才能完全求解，而胡克定律就是这样一个方程。

例如，考虑一个两端固定的柱子，并在中心施加一个载荷P。现在，我们知道在两端作用着反力R₁和R₂。此外，使用力的平衡，我们有R₁ + R₂ = P。这里我们有两个未知数，R₁和R₂，但只有一个方程。我们可以应用胡克定律，以及位移Δ₁和Δ₂，其中Δ₁ = R₁L/2AE和Δ₂ = R₂L/2AE。第二个方程是Δ₁ = Δ₂，因为支座是固定的。因此，我们可以解决这个问题。

有限元法

考虑一根具有不同横截面积A_i和长度L_i的杆，使得每一截面都有一个等效的弹簧常数A_iE/L_i。如果每个节点（面积变化处）的力为F_i，那么我们可以根据每个节点的位移和每一段的弹簧常数写出关于力F_i的方程。如果梁两端固定，则力只能作用于其他节点。

在一般情况下，如果您有载荷作用于连接的细杆上，您可以使用这种方法来求解力和变形。整个结构可以被离散化，并且节点被编号，以便我们得到矩阵[k_ij]。

这种将复杂问题分解成大量简单问题的方法称为有限元法。

各个部分称为单元，在上述情况下，我们使用了线单元。对于一般2-D问题，我们至少需要使用三角形单元。典型问题的矩阵将包含数百个这样的单元，矩阵的大小与单元的数量相同。但是，由于大多数成员都是零，因此该矩阵称为稀疏矩阵，并且可以比您在数学课程中遇到的典型矩阵快得多地求解。

圣维南原理

到目前为止，我们一直在处理作用在梁两端的点载荷。我们假设应力与σ_av = P/A相同。但是，这在载荷作用点附近是不正确的。圣维南原理（由法国弹性学家圣维南提出）指出，远离载荷作用点的应力不受结构在载荷作用点附近精确行为的影响。在所示的图中，这意味着尽管 A-A 处的应力场可能难以计算，但在 B-B 处，应力可以近似为 P/A。S-V 原理与多年的实验和分析相一致，但尚未得到证明。

应力集中系数

到目前为止，我们假设横截面中所有点的应力都相同，并且大体上是正确的。但是，在点载荷和不连续性附近，应力会增加。峰值载荷是根据先前方法计算的平均应力的函数。正确的峰值载荷只能通过有限元分析等方法获得。但是，已经为几种典型场景发布了图表。如前所述，峰值应力σ_p是平均应力σ_av的函数。现在，我们有σ_p = K×σ_av，其中K称为应力集中系数，可以从表格中查阅常见场景。应力集中系数的研究也是一项设计指南，并指示了在现实世界中应避免的特征类型。例如，圆角半径的应力集中系数在r < 0.1 d之外迅速增加，因此您应该为您的轴指定较大的圆角半径或消除直径的变化。

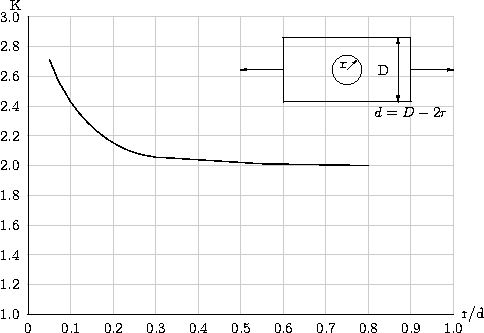
上图显示了带孔板的应力集中比K的可能值。最窄截面的应力是根据d = D − 2r计算的，其中r是孔的半径，D是板的宽度。可以看出，应力集中直到大约r/d = 0.3才显着。

请注意，由于材料的塑性流动，局部应力可能不如应力集中系数所暗示的那样高，因为应力集中分析是针对弹性流动的。

广义胡克定律

泊松比显示当一个方向发生一定变化时，另一个方向上发生的尺寸变化量。每个方向上的应变是所有应变的叠加——直接应变和由于泊松比引起的应变。因此，我们可以将广义胡克定律表述如下

$\epsilon _{x}={\sigma _{x} \over E}-{\nu \sigma _{y} \over E}-{\nu \sigma _{z} \over E}$

$\epsilon _{y}={\nu \sigma _{x} \over E}-{\sigma _{y} \over E}-{\nu \sigma _{z} \over E}$

$\epsilon _{z}={\nu \sigma _{x} \over E}-{\nu \sigma _{y} \over E}-{\sigma _{z} \over E}$

$\gamma _{xy}={\tau _{xy} \over G}$

$\gamma _{yz}={\tau _{yz} \over G}$

$\gamma _{zx}={\tau _{zx} \over G}$

请注意，这些方程仅适用于各向同性材料（钢、铝、铜等），其弹性特性在所有方向上都相同。

模量之间的关系

考虑一个元素，其上分别沿x和y方向作用着应力σ₁和σ₂。现在进一步考虑σ₁ = σ和σ₂ = −σ。

剪切模量可以用杨氏模量表示

$G={\frac {E}{2\left(1+\nu \right)}}$

考虑一个正在经历压缩的物体，因此其应变分别为ε_x、ε_y和ε_z。体积的分数变化因此为ε_x + ε_y + ε_z。应用胡克定律的广义形式，我们得到，体积模量k由下式给出：

$k={\frac {E}{3\left(1-2\nu \right)}}$

压力容器

在不同于周围环境的压力下输送、储存或接收流体的容器、罐和管道称为压力容器。压力容器通常是薄壁结构，包含高压流体。设计决策是为给定的最大压力p找到压力容器厚度t的值。由于厚度远小于容器半径r，因此内半径和外半径被认为相等。对于纵向，我们有压力πr²p产生的力。这由壁中产生的应力平衡，作用在圆的周长2πrtσ上。因此纵向的应力为pr/2t。对于切向，压力力为π2rl，应力力为2tlσ。应力为pr/t。

强度的具体方面

脆性材料

当对于某个特定属性，材料在测量数据中显示出较大的离散度（例如，脆性材料或厚度变化较大的螺纹的强度测量结果），可以通过基于三参数威布尔统计分析测量数据来获得该属性的特征值或最弱环节。