跳到内容

结构生物化学/点群

Add links
来自维基教科书，开放的书籍，为开放的世界
< 结构生物化学
此页面可能需要审查质量。

每个分子都有一组对称操作，描述分子的整体对称性。这组对称性用于对分子进行分类，被称为点群。群论是确定复杂分子对称性、性质和数据的强大数学工具。如果分子在同一组操作下具有相同的对称响应，则它们被称为属于同一个点群。也就是说，两个分子可以具有完全不同的形状，但只要它们对某些对称操作的响应相同，就属于同一个点群。一个分子只能属于一个点群。它不能属于多个点群。

重要的是要理解，点群是用来对分子可能具有的不同对称性进行分类的工具。它试图根据分子的形状和对称性对分子进行分类。有各种对称元素用于阐明分子的形状。分子的形状和对称性在结构生物化学中非常重要，因为结构决定了蛋白质和分子的功能。还需要注意的是，许多分子不断发生构象变化，因此它们的点群也会发生变化。点群是我们在分子水平上理解对称性的工具。[1]

点群类型

[编辑 | 编辑源代码]

分子可以根据它们所包含的对称元素进行区分。不同的对称操作可以被分类为

氨

-旋转操作 (Cn): 绕旋转轴旋转 360/n 度，使物体保持不变。例如，氨 (NH3) 含有三倍旋转轴，赋予其 C3 操作。物体或分子可以拥有多个旋转轴。拥有多个旋转轴的物体示例包括雪花或八面体。

雪花

-反射操作 (σ): 是通过镜面反射，物体在反射时保持不变。存在三种不同的 σ。第一种是 σv，其中镜面平行于主旋转轴和一个外原子。σd 是一个也平行于主旋转轴的镜面，但它不穿过外原子，而是位于两个外原子之间。Td 和 Dnd 的一个例外是，其中所有镜面都称为 σd。最后一个镜面是水平反射 σh，其中反射平面垂直于主旋转轴。主旋转轴是具有最多旋转对称折叠的轴。物体和分子也可以拥有多个反射平面。

File:Sigma v.jpg
σv
File:Sigma d.jpg
σd
File:Sigma h.jpg
σh

-反演操作 (i): 是 C2 旋转和 σh 操作的组合，通过反演点将分子反转，反演点通常取为分子的中心。它是通过物体或分子的中点（中心）的反射（或反转）。

-不当旋转 (Sn): 是旋转 360/n，然后通过垂直于旋转轴的平面反射，σh。S2 操作等同于反演（两者都是 180 度旋转，然后是通过垂直水平轴的反射）。

-恒等 (E): 仅仅是绕任意轴旋转 360 度，得到等效构型。每个分子至少有一个 E 操作。

示例

[编辑 | 编辑源代码]

Oh – 八面体点群 – 包含完美八面体的所有对称元素和操作。

图 I. 八面体。

C∞v : 无限数量的平行于无限数量的旋转轴的镜面。


D∞v : 不仅拥有无限数量的旋转轴和镜面，而且还拥有垂直于这些无限数量的旋转轴的二倍旋转轴。D∞v 还拥有反演中心。

C3v 存在一个三倍主旋转轴和 3 个平行于该轴的镜面。

D3h 指示存在 3 个垂直于三倍主轴的二倍旋转轴和一个垂直于该主轴的镜面。


如何使用点群流程图

[编辑 | 编辑源代码]

所有分子都具有一定的对称性或不对称性，并且可以被分组到类别中（称为点群），其中所有具有相同对称性的分子都属于同一个点群。为了便于确定分子的点群，而无需详尽地确定其所有对称性质，可以使用点群流程图。可以通过逻辑的方式找到分子中包含多少个旋转和镜面来轻松地确定分子的点群。物体对称性越低，确定其点群所需的对称操作就越困难，而对称性越高就越容易确定。这允许用户根据分子的形状来回答简单的问题。如果一个人能够理解点群流程图，就不需要记忆。因此，点群确定非常简单，只需要了解点群类型和一些可视化。[2]

存在许多其他点群，如 C4v、C5v、D4h、D5h 等。记忆所有点群的定义非常繁琐。为了简化这一点，可以通过遵循流程图轻松地找到分子的点群。首先，确定分子是线性的还是非线性的。如果是线性的，则确定是否存在反演中心。如果分子是非线性的，则检查是否存在两个或更多个 Cn，其中 n 大于 2。如果是，则确定是否存在反演中心以及是否存在 C5 旋转轴。如果存在两个或更多个 Cn，则检查是否存在任何 Cn。如果有，则检查具有较高 n 的 Cn 是否垂直于 nC2。如果是，则确定分子是否具有 σh 或 σd。如果不存在两个或更多个 Cn，则检查是否存在 σh、nσv 或 S2n。这些是存在 Cn 的情况，但如果不存在任何 Cn，则检查是否存在 σh 或反演中心。如果正确完成此操作，到达链的末端将是观察到的分子的点群。

Point Group Flow Chart
点群流程图

如何使用流程图的示例

[编辑 | 编辑源代码]
File:Water molecule like Micky mouse.png
水分子

以上是水分子图。遵循流程图：1. 该分子是非线性的 2. 该分子除了主轴之外没有超过 2 个旋转轴 3. 该分子具有适当的 C2 主旋转轴 4. 但该分子没有 2 个垂直于主旋转轴的其他适当旋转轴 5. 该分子没有垂直于主轴的镜面 6. 该分子有两个平行于主轴的镜面 7. 因此，水分子属于 C2v 点群。

File:BF5.png
BF5 分子

以上是 BF5 分子图。遵循点群流程图：1. 该分子是非线性的 2. 该分子除了主旋转轴之外没有超过 2 个旋转轴 3. 该分子具有 4 倍适当旋转轴 4. 该分子没有 4 个垂直于主旋转轴的 C2 轴 5. 该分子没有垂直于主旋转轴的镜面 6. 该分子有 4 个垂直于主旋转轴的镜面 7. 因此，该分子属于 C4v 点群。

File:Cyclopropane molecular orbital.png
环丙烷

以上是环丙烷分子图。遵循点群流程图：1. 该分子是非线性的 2. 该分子除了主旋转轴之外没有超过 2 个旋转轴 3. 该分子具有适当的 3 倍旋转轴 4. 该分子有 3 个垂直的 C2 轴 5. 该分子有垂直于主旋转轴的镜面 6. 因此，该分子属于 D3h 点群。

File:Cyclopropane molecular orbital.png
八氯化锇

上面是一个八氯锇分子，以重叠构象存在。遵循流程图：1. 该分子不是线性的。2. 该分子除了主要旋转轴外，没有超过2个旋转轴。3. 该分子具有C4真旋转轴。4. 该分子具有4个C2真旋转轴，它们垂直于主要旋转轴。5. 该分子没有垂直于主要旋转轴的镜面。6. 该分子具有4个平行于主要旋转轴的镜面。7. 因此，该分子属于D4d点群。


高对称点群

[编辑 | 编辑源代码]

高对称分子具有特定的几何形状，例如线性、八面体 (Oh)、四面体 (Td) 和二十面体 (Ih) 形状。虽然这些对称性存在一些变体，但在自然界中并不常见。

-C∞v 是线性分子，沿主要旋转轴有无限多个旋转，以及包含旋转轴的无限多个反射平面。它们没有反转中心，通常是双原子分子。

-D∞h 也是线性分子，沿主要轴有无限多个旋转，以及包含旋转轴的无限多个反射平面。与C∞v 的三个主要区别是，存在一个垂直于主要旋转轴的C2 轴和一个反射平面，以及一个反转中心。

-Td 分子具有四面体几何形状（但不一定具有四面体的形状）。它们有4个C3 轴、3个C2 轴、3个S4 轴和6个镜面。但是，它们缺少C4 轴。

-Oh 分子最常见的是那些具有八面体结构的分子。它们通常具有4个C3 旋转、3个C4 旋转和一个反转中心。

-Ih 分子通过它们的C3 和C5 轴以及反转中心来识别。

低对称点群

[编辑 | 编辑源代码]

C1 是一个除了恒等运算 E 外没有其他对称性的分子。Cs 是一个只有镜面和恒等运算 E 的分子。Ci 仅包含反转中心和恒等运算 E。

特定点群示例

[编辑 | 编辑源代码]
群 Intl Orbifold Coxeter 阶 描述
Cn n nn [n]+ n 循环：n 阶旋转。抽象群 Zn，模 n 加法的整数群。
Dn nm *nn [n] 2n 二面体：循环加反射。抽象群 Dihn，二面体群。
有限同构和对应关系

由1或2个镜面定义的纯反射点群子集，也可以通过它们的考克斯特群和相关多边形给出。这些包括5个晶体学群。反射群的对称性可以通过一个同构来加倍，通过一个平分镜将两个镜面都映射到彼此，使对称性阶加倍。

反射的 旋转的 相关多边形
群 考克斯特群 考克斯特图 阶 子群 Coxeter 阶
D1 A1 [ ] Template:CDD Template:CDD 2 C1 []+ 1 二角形
D2 A12 [2] Template:CDD Template:CDD 4 C2 [2]+ 2 矩形
D3 A2 [3] Template:CDD Template:CDD 6 C3 [3]+ 3 等边三角形
D4 BC2 [4] Template:CDD Template:CDD 8 C4 [4]+ 4 正方形
D5 H2 [5] Template:CDD Template:CDD 10 C5 [5]+ 5 正五边形
D6 G2 [6] Template:CDD Template:CDD 12 C6 [6]+ 6 正六边形
Dn I2(n) [n] Template:CDD Template:CDD 2n Cn [n]+ n 正多边形
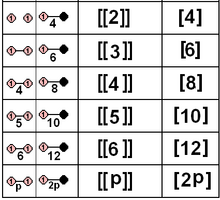
D2×2 A12×2 [[2]] = [4] Template:CDD Template:CDD = Template:CDD 8
D3×2 A2×2 [[3]] = [6] Template:CDD Template:CDD = Template:CDD 12
D4×2 BC2×2 [[4]] = [8] Template:CDD Template:CDD = Template:CDD 16
D5×2 H2×2 [[5]] = [10] Template:CDD Template:CDD = Template:CDD 20
D6×2 G2×2 [[6]] = [12] Template:CDD Template:CDD = Template:CDD 24
Dn×2 I2(n)×2 [[n]] = [2n] Template:CDD Template:CDD = Template:CDD 4n
Intl* Geo
[3] 		Orbifold Schönflies Conway Coxeter 阶
1 1 1 C1 C1 [ ]+ 1
1 22 ×1 Ci = S2 CC2 [2+,2+] 2
2 = m 1 *1 Cs = C1v = C1h ±C1 = CD2 [ ] 2
2
3
4
5
6
n		 2
3
4
5
6
n 		22
33
44
55
66
nn		 C2
C3
C4
C5
C6
Cn		 C2
C3
C4
C5
C6
Cn		 [2]+
[3]+
[4]+
[5]+
[6]+
[n]+
 2
3
4
5
6
n
2mm
3m
4mm
5m
6mm
nmm
nm		 2
3
4
5
6
n		 *22
*33
*44
*55
*66
*nn		 C2v
C3v
C4v
C5v
C6v
Cnv		 CD4
CD6
CD8
CD10
CD12
CD2n		 [2]
[3]
[4]
[5]
[6]
[n]		 4
6
8
10
12
2n
2/m
3/m
4/m
5/m
6/m
n/m		 2 2
3 2
4 2
5 2
6 2
n 2 		2*
3*
4*
5*
6*
n*		 C2h
C3h
C4h
C5h
C6h
Cnh		 ±C2
CC6
±C4
CC10
±C6
±Cn / CC2n		 [2,2+]
[2,3+]
[2,4+]
[2,5+]
[2,6+]
[2,n+]		 4
6
8
10
12
2n
4
3
8
5
12
2n
n 		4 2
6 2
8 2
10 2
12 2
2n 2 		2×
3×
4×
5×
6×
n×		 S4
S6
S8
S10
S12
S2n		 CC4
±C3
CC8
±C5
CC12
CC2n / ±Cn		 [2+,4+]
[2+,6+]
[2+,8+]
[2+,10+]
[2+,12+]
[2+,2n+]		 4
6
8
10
12
2n
Intl Geo Orbifold Schönflies Conway Coxeter 阶
222
32
422
52
622
n22
n2		 2 2
3 2
4 2
5 2
6 2
n 2		 222
223
224
225
226
22n		 D2
D3
D4
D5
D6
Dn		 D4
D6
D8
D10
D12
D2n		 [2,2]+
[2,3]+
[2,4]+
[2,5]+
[2,6]+
[2,n]+		 4
6
8
10
12
2n
mmm
6m2
4/mmm
10m2
6/mmm
n/mmm
2nm2		 2 2
3 2
4 2
5 2
6 2
n 2		 *222
*223
*224
*225
*226
*22n		 D2h
D3h
D4h
D5h
D6h
Dnh		 ±D4
DD12
±D8
DD20
±D12
±D2n / DD4n		 [2,2]
[2,3]
[2,4]
[2,5]
[2,6]
[2,n]		 8
12
16
20
24
4n
42m
3m
82m
5m
122m
2n2m
nm		 4 2
6 2
8 2
10 2
12 2
n 2
 2*2
2*3
2*4
2*5
2*6
2*n		 D2d
D3d
D4d
D5d
D6d
Dnd		 ±D4
±D6
DD16
±D10
DD24
DD4n / ±D2n		 [2+,4]
[2+,6]
[2+,8]
[2+,10]
[2+,12]
[2+,2n]		 8
12
16
20
24
4n
23 3 3 332 T T [3,3]+ 12
m3 4 3 3*2 Th ±T [3+,4] 24
43m 3 3 *332 Td TO [3,3] 24
432 4 3 432 O O [3,4]+ 24
m3m 4 3 *432 Oh ±O [3,4] 48
532 5 3 532 I I [3,5]+ 60
53m 5 3 *532 Ih ±I [3,5] 120
(*) 当 Intl 条目重复时，第一个对应偶数 n，第二个对应奇数 n。

反射子集群

[编辑 | 编辑源代码]
有限同构和对应关系

由1到3个镜面定义的纯反射点群子集，也可以通过它们的考克斯特群和相关多面体给出。[3,3] 群可以加倍，写成 [[3,3]]，将第一个和最后一个镜面映射到彼此，使对称性加倍至 48，并且与 [4,3] 群同构。

Schönflies 考克斯特群 考克斯特图 阶 相关正多面体和棱柱体
Td A3 [3,3] Template:CDD 24 四面体
Td×Dih1 = Oh A3×2 = BC3 [[3,3]] = [4,3] Template:CDD = Template:CDD 48 星形八面体
Oh BC3 [4,3] Template:CDD 48 立方体，八面体
Ih H3 [5,3] Template:CDD 120 二十面体，十二面体
D3h A2×A1 [3,2] Template:CDD 12 三角棱柱
D3h×Dih1 = D6h A2×A1×2 [[3],2] Template:CDD = Template:CDD 24 六角棱柱
D4h BC2×A1 [4,2] Template:CDD 16 正方棱柱
D4h×Dih1 = D8h BC2×A1×2 [[4],2] = [8,2] Template:CDD = Template:CDD 32 八角柱
D5h H2×A1 [5,2] Template:CDD 20 五角柱
D6h G2×A1 [6,2] Template:CDD 24 六角棱柱
Dnh I2(n)×A1 [n,2] Template:CDD 4n n-边 棱柱
Dnh×Dih1 = D2nh I2(n)×A1×2 [[n],2] Template:CDD = Template:CDD 8n
D2h A13 [2,2] Template:CDD 8 长方体
D2h×Dih1 A13×2 [[2],2] = [4,2] Template:CDD = Template:CDD 16
D2h×Dih3 = Oh A13×6 [3[2,2]] = [4,3] Template:CDD = Template:CDD 48
C3v A2 [1,3] Template:CDD 6 正多面体
C4v BC2 [1,4] Template:CDD 8
C5v H2 [1,5] Template:CDD 10
C6v G2 [1,6] Template:CDD 12
Cnv I2(n) [1,n] Template:CDD 2n
Cnv×Dih1 = C2nv I2(n)×2 [1,[n]] = [1,2n] Template:CDD = Template:CDD 4n
C2v A12 [1,2] Template:CDD 4
C2v×Dih1 A12×2 [1,[2]] Template:CDD = Template:CDD 8
Cs A1 [1,1] Template:CDD 2

表示

[编辑 | 编辑源代码]

不可约表示用于为该点群创建字符表。

- 值为 1 表示对称性不会改变其轨道位置

- 值为 0 表示操作会改变轨道的 位置

- 值为 -1 表示轨道不会改变其对称性，但会反转其符号。

可约表示只是不可约表示的组合。

字符表

[编辑 | 编辑源代码]

字符表由这些字符指定，这些字符意味着不同的操作。

-x,y,x 是 x,y,z 坐标的变换

-Rx, Ry, Rz 是围绕 x, y, z 轴的旋转

-R 是任何对称操作，如 C2

-X 是操作的特征

-i, j 是不同表示的名称，例如 A1 或 A2

-h 是组中对称操作的总数（阶数）

参考文献

[编辑 | 编辑源代码]
  1. ↑ 点群，2012 年 11 月 14 日。
  2. ↑ 点群，2012 年 10 月 28 日
  3. ↑ 几何代数中的晶体空间群，D. Hestenes 和 J. Holt，数学物理学杂志。 48, 023514 (2007) (22 页) PDF [1]

http://en.wikipedia.org/wiki/Point_group

Miessler, Gary. 无机化学。 第四版。

检索自 "https://wikibooks.cn/wiki/Structural_Biochemistry/Point_Groups"
华夏公益教科书