面积和体积 是空间几何学的一个主题,它处理三维几何体积的体积和面积的性质、特征、应用和计算。三维体积是具有三个维度(长度、宽度、高度)的物体。
旋转、截面、切割、三维绘图、体积的扩展绘图、封闭、体积和面积是该主题的重要元素。
几何体积分为两类
棱柱、球体、锥体等几何体积。
非几何体积 体积 :物体所占空间的大小称为体积。体积单位等于立方单位。体积是三维空间的量,它由特定边界限制,例如,它是由物质(固体、气体、液体、等离子体)或其形状所占的空间。体积是 SI 的子单位,它是米的三次方(立方米)。容器的体积等于装满它的液体的体积。为了计算某些三维形状的体积,存在特定关系,这些关系对于具有几何规律的简单形状来说是简单的关系。对于没有简单关系来计算体积的复杂形状,可以通过积分方法获得体积。一维形状(如线)或二维形状(如平面)的体积为零。
面积 :它是一种计算三维物体表面值和二维物体内部值的量。面积单位等于平方单位。面积是表示平面或曲面上区域大小的量。平面区域或“平面面积”是指平面层或层的面积,而“表面积”是指三维物体开放表面或边界的面积。面积可以理解为形成形状模型所需的给定厚度的材料量,或者用一层涂料覆盖表面所需的涂料量。这种二维类比是一条曲线(一维概念)的长度或一个固体(三维概念)的体积。
非几何体积 =非几何体积是体积难以获得的复杂体积。但它们的面积可以获得,但有点复杂。为了获得非几何体积,我们首先在烧杯中倒入水。在我们用它装满水并测量体积后,我们将非几何物体放入水中。水会上升,然后我们将非几何体积使水上升的体积与之前测定的水体积相减,然后测量并记录其体积。
几何体积 =几何体积是可以为其写出表面积和体积公式的物体。我们可以通过分析和测量相应分量的体积,通过模式查找方法找到这些几何物体的体积。然后通过总结和公式化,我们可以得到其体积的公式。为了找到它的面积,我们首先通过分析和以连续和离散的方式绘制形状来计算其分量的面积,并通过分析写出其公式。
例子 = 球体、锥体、棱柱、多面体、圆柱体、圆锥体和立方体、四面体、平行四边形
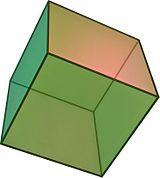
说明 1:规则多面体(六面体)立方体有一个正方形面,它有两个正方形底面,因此立方体是一个规则的棱柱-多面体体积。
说明 2:四面体是一个金字塔,也是一个多面体,其底面和侧面为等边三角形。因此,四面体被认为是一个金字塔-多面体体积,也是一种柏拉图立体。
要点 3:平行四边形是一个具有侧面和为六边形的棱柱体积,其侧面平行。因此,平行四边形是一个棱柱-多面体体积。
棱柱的定义 :棱柱是一个具有两个底面、侧面、顶点和边的体积。棱柱的面是矩形,面的数量等于底面的边数,顶点的数量是面的数量的两倍,边的数量是棱柱面的三倍。棱柱的面的数量通过公式 n+2 获得,因为棱柱中心的面的数量总是比侧面的数量多两个,因为另外两个面是棱柱的底面。在另一个平面中)和 n 个其他面,这些面必然都是平行四边形,并将两个 n 边形的对应顶点连接起来。所有平行于底面的横截面都是相同的。棱柱根据其底边数命名;因此,例如,具有五边形底面的棱柱称为五边形棱柱。棱柱与金字塔的定义是,棱柱与金字塔相同,但其顶点位于无穷远处。
锥体的定义 :锥体是一个体积,其面在一个点处相交,并且其面为三角形,其底面为三角形。边的数量是底面。实际上,锥体是通过将空间中的一个点连接到平面上所有封闭形状点的点而创建的三维形状。该点称为锥体顶点,该平面形状称为锥体底面。锥体的底面是一个任意的多边形,其他面是连接到顶点的等边三角形。连接顶点和底面的垂线称为锥体的高度。在世界上最著名的金字塔形结构中,我们可以提到埃及的三座金字塔。
球体的定义 :球体是三维空间中的一个完全圆形的几何物体。例如,球体是一个球体。球体就像二维空间中的圆一样,在三维空间中的一个点周围完全对称。球体表面上的所有点都与球体中心相距相等。这些点到球体中心的距离称为球体的半径,用字母 r 表示。球体两侧的最长距离(穿过球体)称为球体的直径。球体的直径也穿过其中心,因此其大小是半径的两倍。球体是空间中的一组点,具有圆形底面和半径,它是一个规则的多面体。球体是半圆和一个圆绕其直径旋转一周的结果,在圆周上旋转 180 度,在半圆周上旋转 360 度。我们根据其面积的划分将球体的面划分为几个度数,它为 360 度。
圆柱体的定义:圆柱体是一种底面为圆形的棱柱体。在几何学中,圆柱体是一种空间曲线底面,其表面由一组点形成。圆柱体的边是不可确定的,因为它的底面是圆形的。也就是说,可以认为圆柱体的侧面、面、顶点、边依次为3n、2n、n+2、n。微分几何中的圆柱体被绘制为生成线为一组平行线的曲面。圆锥体中圆柱体的定义与圆锥体相同,但其顶点在无穷远处。圆柱体是由一个矩形绕其一侧(长、宽)旋转360度得到的。
圆锥体的定义:圆锥体是一种底面为圆形的锥体,圆锥体是一种三维几何图形,从其平坦的底面(圆锥体截面)到顶点,缓慢或快速(取决于底面和高度)地变窄。更确切地说,它是由一个底平面(圆锥体截面)和一个侧面所包围的固体形状,该侧面是连接圆锥体顶点与底面周围点的直线的轨迹。圆锥体一词有时指的是该固体的顶点,有时仅指其侧面。圆锥体可以是直立的或倾斜的。必须提到的是,具有特定截面积和特定高度的斜圆锥的体积等于具有相同面积和特定高度的直圆锥的体积。由直角三角形绕其一边(邻边)旋转360度得到的圆锥体。
多面体的定义:多面体是三维空间中的一个立体几何体,具有平面面(每个面在一个平面内)和位于直线上的边或棱。迄今为止,还没有为它提供单一的定义。四面体是一种金字塔,立方体是六面体的例子。多面体可以是凸的或非凸的。金字塔和棱柱等多面体可以通过挤压二维多边形来制作。具有规则面和等角形状的凸多面体只有有限个,包括柏拉图立体和阿基米德立体。一些阿基米德立体可以通过切割柏拉图立体的顶部金字塔来制作。由于构造的简单性,多面体在大多数建筑作品中使用,例如测地线圆顶和金字塔。近年来,由于形状的使用,对多面体表面的兴趣不断增加。一些紧凑的分子和原子,特别是晶体结构和柏拉图烃,以及一些径向具有与柏拉图立体相似的形状。柏拉图立体也被用于制作骰子。多面体具有不同的特征和类型,并被置于不同的对称群中。其他多面体可以通过对任何多面体进行操作来创建。其中一些彼此之间存在关系。多面体自石器时代以来就一直受到人们的关注。球体也被认为是多面体家族的一部分。立方体、四面体、平行四边形都是几何体,也被认为是多面体。
立方体的体积: V = a 3 {\displaystyle V=a^{3}\;}
立方体的表面积: V = 6 a 2 {\displaystyle V=6a^{2}\;}
四面体的体积: V = 2 12 a 3 {\textstyle V={{\sqrt {2}} \over 12}a^{3}\,}
四面体的表面积: V = 3 a 2 {\displaystyle V={{\sqrt {3}}a^{2}\,}}
正八面体的体积
V = 2 3 a 3 {\displaystyle V={\frac {2}{3}}a^{3}}
正八面体的表面积
V = 2 a 2 3 {\displaystyle V={2a^{2}{\sqrt {3}}\,}}
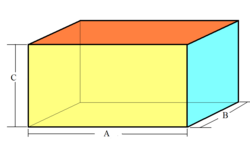
长方体的体积: V = a b c {\textstyle {V=abc}}
长方体的表面积: A = 2 a b + 2 a c + 2 c b {\textstyle A=2ab+2ac+2cb}
棱柱体的体积: V = S h {\displaystyle V=Sh}
多边形底棱柱体的体积: V = n 4 h a 2 cot π n {\displaystyle V={\frac {n}{4}}ha^{2}\cot {\frac {\pi }{n}}}
多边形底棱柱体的表面积: A = n 2 a 2 cot π n + n a h {\displaystyle A={\frac {n}{2}}a^{2}\cot {\frac {\pi }{n}}+nah}
圆柱体的体积: V = π r 2 h {\displaystyle {\displaystyle V=\pi r^{2}h}}
圆柱体的侧面积: A = P h + 2 S {\displaystyle A=\ Ph+2S}
圆柱体面积: A = 2 π r ( r + h ) {\displaystyle A=2\pi r(r+h)\,\!}
金字塔的体积: V = 1 3 S h {\displaystyle V={\displaystyle {\frac {1}{3}}Sh}}
圆锥的体积: V = 1 3 π r 2 h {\displaystyle V={\frac {1}{3}}\pi r^{2}h}
金字塔的面积: B + P L 2 {\displaystyle B+{\frac {PL}{2}}\,\!}
圆锥的面积: π r ( r + l ) {\displaystyle \pi r(r+l)\,\!}
球体的体积: V = 4 3 π r 3 {\displaystyle V={\frac {4}{3}}\pi r^{3}}
球体的面积: 4 π r 2 or π d 2 {\displaystyle 4\pi r^{2}\ {\text{or}}\ \pi d^{2}\,\!}
球形体积: 4 3 π r 2 h {\displaystyle {4 \over 3}\pi r^{2}h}
椭球体积: 4 3 π a b c {\displaystyle {4 \over 3}\pi abc}
球形面积= A = 4 π a b {\displaystyle {A=4\pi ab}}
椭圆面积=: A = 2 π a 2 ( 1 + c a e arcsin e ) {\displaystyle A=2\pi a^{2}\left(1+{\frac {c}{ae}}\arcsin e\right)}
不完整金字塔的体积: V = 1 3 h ( a 2 + a b + b 2 ) . {\displaystyle V={\tfrac {1}{3}}h\left(a^{2}+ab+b^{2}\right).}
不完整金字塔的面积: A = n 4 [ ( a 1 2 + a 2 2 ) cot π n + ( a 1 2 − a 2 2 ) 2 sec 2 π n + 4 h 2 ( a 1 + a 2 ) 2 ] {\displaystyle A={\frac {n}{4}}\left[\left(a_{1}^{2}+a_{2}^{2}\right)\cot {\frac {\pi }{n}}+{\sqrt {\left(a_{1}^{2}-a_{2}^{2}\right)^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}\left(a_{1}+a_{2}\right)^{2}}}\right]}
不完全圆锥体积: V = π 3 h ( r 2 + r r ′ + r ′ 2 ) . {\displaystyle {\displaystyle V={\tfrac {\pi }{3}}h\left(r^{2}+rr'+r'^{2}\right).}}
不完全圆锥表面积: Total surface area = = π ( ( r 1 + r 2 ) ( r 1 − r 2 ) 2 + h 2 + r 1 2 + r 2 2 ) {\displaystyle {\displaystyle {\begin{aligned}{\text{Total surface area}}&=\\&=\pi \left(\left(r_{1}+r_{2}\right){\sqrt {\left(r_{1}-r_{2}\right)^{2}+h^{2}}}+r_{1}^{2}+r_{2}^{2}\right)\end{aligned}}}}
圆环体积: V = 2 π 2 R r 2 = ( π r 2 ) ( 2 π R ) . {\displaystyle V=2\pi ^{2}Rr^{2}=\left(\pi r^{2}\right)\left(2\pi R\right).\,}
圆环面积: A = 4 π 2 R r = ( 2 π r ) ( 2 π R ) {\displaystyle A=4\pi ^{2}Rr=\left(2\pi r\right)\left(2\pi R\right)\,}
平行六面体体积: V = a b c K {\displaystyle V=abc{\sqrt {K}}}
平行六面体表面积: 2 ( a h + b h ′ + c h ″ ) {\displaystyle 2{(ah+bh'+ch'')}}
正多面体面积
A = n ( 1 4 n ′ a 2 cot π n ′ ) {\displaystyle A=n({\tfrac {1}{4}}n'a^{2}\cot {\frac {\pi }{n'}})}
多面体体积: 1 3 | ∑ F ( Q F ⋅ N F ) Area ( F ) | , {\displaystyle {\frac {1}{3}}\left|\sum _{F}(Q_{F}\cdot N_{F})\operatorname {Area} (F)\right|,}
表面积与体积之比,用 sa/vol 或 SA:V 表示,是指物体或物体集合的每个体积单位所对应的表面积。在涉及固体物质的化学反应中,表面积与体积之比是一个重要的因素,它表明化学反应正在进行。表面积与体积之比或 SA:V 是一个公式,它表示体积与总表面积之比,其数值在不同的几何体中是不同的。SA:V 比值取决于半径的大小或几何体的大小。
V/S立方体比例: a 6 {\displaystyle {\frac {a}{6}}}
四面体 V/S 比例: 2 12 a 3 2 a 2 3 {\displaystyle {\frac {{{\sqrt {2}} \over 12}a^{3}}{2a^{2}{\sqrt {3}}}}}
V/S 比例: S h P h + 2 s {\displaystyle {\frac {Sh}{Ph+2s}}}
圆柱体的 V/S 比例: π r 2 h 2 π r 2 + 2 π r h {\displaystyle {\frac {\pi r^{2}h}{2\pi r^{2}+2\pi rh}}}
金字塔的 V/S 比例: 1 3 S h N 2 B h + S {\displaystyle {\frac {{\frac {1}{3}}Sh}{{\frac {N}{2}}Bh+S}}}
圆锥的 V/S 比例: 1 3 π r 2 h π r 2 + π r L {\displaystyle {\frac {{\frac {1}{3}}\pi r^{2}h}{\pi r^{2}+\pi rL}}}
球体的 V/S 比例= r 3 {\displaystyle {\frac {r}{3}}}
一个三维球体的表面积与体积比值 (SA:V) 值图,显示了球体半径增大。球体半径与比例成反比关系。 球体是一个三维物体,形状为球形(在本主题中,球体上的大部分面积(面积)是需要的,而不是它内部的体积)。球体可以存在于任何需要的维度,并且通常被称为 n 维球体,其中 n 是球体的维度数。对于典型的三维球体,SA:V 可以使用面积和体积的标准公式计算;其中面积 i s S = 4 π r 2 {\displaystyle isS=4\pi r^{2}} i s V = ( 4 / 3 ) π r 3 {\displaystyle isV=(4/3)\pi r^{3}}
上述论点可以扩展到 n 维球体,并且可以写出体积和表面积的一般关系,如下所示
V = r n π n 2 Γ ( 1 + n / 2 ) {\displaystyle V={\frac {r^{n}\pi ^{\frac {n}{2}}}{\Gamma (1+n/2)}}} S = n r n − 1 π n 2 Γ ( 1 + n / 2 ) {\displaystyle S={\frac {nr^{n-1}\pi ^{\frac {n}{2}}}{\Gamma (1+n/2)}}}
比率 V S {\displaystyle {\frac {V}{S}}} n r − 1 {\displaystyle nr^{-1}}
这些主题是对列表的部分证明,以及对其公式证明的参考。要查看完整的证明,您应该阅读补充数学中几何部分关于三维几何形状的部分。
立方体的体积像长方体的体积一样,但由于立方体的边是相等的,它被放置在它边的三次方上。
V = S . H = ( a 2 ) . a = a 3 {\displaystyle V=S.H=(a^{2}).a=a^{3}}
立方体的表面积也可以用不同的方法证明,我们知道立方体有六个正方形的面,它们都是规则的四边形,它的总面积是根据立方体的六个正方形面的总和得到的。立方体的总面积,就像立方体的体积一样,是通过棱柱公式得到的,并且根据棱柱的总面积来证明。
V = P . H + 2 S = 4 a 2 + 2 a 2 = 6 a 2 {\displaystyle V=P.H+2S=4a^{2}+2a^{2}=6a^{2}}
平行六面体的体积是根据三个向量 a、b、c 得到的,这三个向量以行列式的形式确定。但首先,它应该用三角函数计算,然后写成行列式。
S = | a | ⋅ | b | ⋅ sin γ = | a × b | {\displaystyle S=\left|\mathbf {a} \right|\cdot \left|\mathbf {b} \right|\cdot \sin \gamma =\left|\mathbf {a} \times \mathbf {b} \right|}
h = | c | ⋅ | cos θ | {\displaystyle h=\left|\mathbf {c} \right|\cdot \left|\cos \theta \right|}
计算完成后,我们将工作写成行列式的形式。
V = | det [ a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 ] | . {\displaystyle V=\left|\det {\begin{bmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{bmatrix}}\right|.}
a → = ( a 1 , a 2 , a 3 ) {\displaystyle {\vec {a}}=(a_{1},a_{2},a_{3})} b → = ( b 1 , b 2 , b 3 ) {\displaystyle {\vec {b}}=(b_{1},b_{2},b_{3})} c → = ( c 1 , c 2 , c 3 ) {\displaystyle {\vec {c}}=(c_{1},c_{2},c_{3})} 平行六面体的体积是这样的。
V = | ( a → . b → ) . c → | = a 1 b 1 c 1 + a 2 b 2 c 2 + a 3 b 3 c 3 {\displaystyle V=|({\vec {a}}.{\vec {b}}).{\vec {c}}|=a_{1}b_{1}c_{1}+a_{2}b_{2}c_{2}+a_{3}b_{3}c_{3}}
棱柱的体积,如果 s 是底面积,h 是高,它的体积是: V = S h {\displaystyle V=Sh}
如果 p 是底面的周长,h 是高,棱柱的侧面积可以相应地写成。
S = P h {\displaystyle S=Ph}
如果 s 是底面积,棱柱的总面积可以根据这个公式写成 S = P h + 2 s {\displaystyle S=Ph+2s}
圆柱是几何学中基本曲面形状之一,其外表面是一组到直线距离相等的点。这条线的名称为中心轴。这种空间形状的两端由垂直于封闭圆柱体轴线的两块板封闭。圆柱体的表面积和体积在很早以前就为数学家所知。
圆柱体的体积是根据棱柱体的体积计算的。
V = S . H = π R 2 H {\displaystyle V=S.H=\pi R^{2}H}
四面体 平行六面体 长方体 棱柱体 棱锥 圆锥 不完整棱锥 球体 







































![{\displaystyle A={\frac {n}{4}}\left[\left(a_{1}^{2}+a_{2}^{2}\right)\cot {\frac {\pi }{n}}+{\sqrt {\left(a_{1}^{2}-a_{2}^{2}\right)^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}\left(a_{1}+a_{2}\right)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57c9ba44195955a9024eca9605b00b44cdbe785a)
































