支持向量机

支持向量机 (SVM) 是一组相关的监督学习方法，用于分析数据和识别模式，用于分类和回归分析。原始的 SVM 算法由弗拉基米尔·瓦普尼克发明，而目前标准的实现形式 (软间隔) 由科林娜·科特斯和弗拉基米尔·瓦普尼克提出。标准的 SVM 是一种非概率二元线性分类器，也就是说，它预测对于每个给定的输入，该输入属于两个可能的类别中的哪一个。由于 SVM 是一种分类器，因此给定一组训练样本，每个样本都标记为属于两个类别之一，SVM 训练算法构建一个模型来预测新样本是否属于一个类别或另一个类别。直观地说，SVM 模型是将样本表示为空间中的点，映射的方式使得不同类别的样本之间存在清晰的间隔，这个间隔尽可能宽。然后将新的样本映射到相同的空间，并根据它们落在间隔的哪一边来预测它们属于哪个类别。

更正式地说，支持向量机在一个高维或无限维空间中构建一个超平面或一组超平面，可用于分类、回归或其他任务。直观地说，可以通过距离任何类别最近的训练数据点距离最大的超平面 (称为函数间隔) 来实现良好的分离，因为通常间隔越大，分类器的泛化误差越低。

尽管原始问题可能在一个有限维空间中表述，但通常情况下，在那个空间中，要区分的集合不是线性可分的。因此，有人提出将原始有限维空间映射到一个更高维的空间，假设在这个空间中分离更容易。SVM 方案使用映射到一个更大的空间，以便能够以原始空间中的变量表示轻松计算交叉乘积，从而使计算负载合理。较大空间中的交叉乘积由内核函数$K(x,y)$ 定义，该函数可以根据问题进行选择。较大空间中的超平面被定义为与该空间中的某个向量交叉乘积为常数的点的集合。定义超平面的向量可以被选择为特征向量图像的线性组合，其参数为$\alpha _{i}$，这些特征向量图像出现在数据库中。有了这种超平面选择，映射到超平面中的特征空间中的点 x 由以下关系定义：$\sum _{i}{\alpha _{i}K(x_{i},x)}=constant$ 请注意，如果$K(x,y)$ 随着 $y$ 距离 $x$ 越来越远而变小，则上述总和中的每个元素都衡量了测试点 $x$ 与相应数据库点 $x_{i}$ 的相对接近程度。这样，上面内核的总和可以用来衡量每个测试点与源自要区分的集合中的一个或另一个的数据库点的相对接近程度。请注意，映射到任何超平面中的点 $x$ 的集合可能相当复杂，因此允许在原始空间中与凸形相去甚远的集合之间进行更复杂的区分。

动机

H3（绿色）无法将 2 类分开。H1（蓝色）可以，但边距很小，而 H2（红色）则具有最大边距。

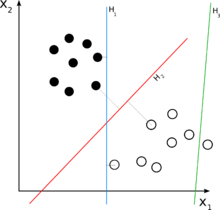
统计分类|分类数据是机器学习中的一项常见任务。假设一些给定的数据点分别属于两个类别之一，目标是确定一个新数据点属于哪个类别。在支持向量机的情况下，数据点被视为一个 $p$-维向量（$p$ 个数字的列表），我们想知道是否可以用一个 $p-1$-维超平面将这些点分开。这被称为线性分类器。存在许多可能对数据进行分类的超平面。一个合理的最佳超平面选择是代表两类之间最大分离或边距的超平面。因此，我们选择超平面，使其到两侧最近数据点的距离最大化。如果这样的超平面存在，它被称为最大边距超平面，它定义的线性分类器被称为最大边距分类器。

形式化

我们得到了一些训练数据 ${\mathcal {D}}$，它是一个包含n个点的集合，这些点的形式为

${\mathcal {D}}=\left\{(\mathbf {x} _{i},c_{i})\mid \mathbf {x} _{i}\in \mathbb {R} ^{p},\,c_{i}\in \{-1,1\}\right\}_{i=1}^{n}$

其中c_i 为 1 或 -1，表示点 $\mathbf {x} _{i}$ 所属的类别。每个 $\mathbf {x} _{i}$ 都是一个 $p$-维实数|实向量。我们想要找到将 $c_{i}=1$ 的点与 $c_{i}=-1$ 的点分开的最大边距超平面。任何超平面都可以写成满足以下条件的点 $\mathbf {x}$ 的集合：

SVM 训练样本来自两个类别，其最大边距超平面和边距。边距上的样本称为支持向量。

$\mathbf {w} \cdot \mathbf {x} -b=0,\,$

其中 $\cdot$ 表示点积。向量 ${\mathbf {w} }$ 是一个表面法线 | 法向量：它垂直于超平面。参数 ${\tfrac {b}{\|\mathbf {w} \|}}$ 决定了超平面相对于原点沿法向量 ${\mathbf {w} }$ 的偏移。

我们想要选择 ${\mathbf {w} }$ 和 $b$ 来最大化间隔，或者说最大化两个平行超平面之间的距离，这两个超平面尽可能地远离彼此，同时仍然将数据分开。这些超平面可以用以下方程描述：

$\mathbf {w} \cdot \mathbf {x} -b=1\,$

和

$\mathbf {w} \cdot \mathbf {x} -b=-1.\,$

注意，如果训练数据是线性可分的，我们就可以选择间隔的两个超平面，使得它们之间没有点，然后尝试最大化它们之间的距离。利用几何学，我们发现这两个超平面之间的距离是 ${\tfrac {2}{\|\mathbf {w} \|}}$，因此我们希望最小化 $\|\mathbf {w} \|$。由于我们还必须防止数据点落入间隔中，因此我们添加以下约束：对于每个 $i$ 都有

$\mathbf {w} \cdot \mathbf {x} _{i}-b\geq 1\qquad {\text{ for }}\mathbf {x} _{i}$ 属于第一类

或

$\mathbf {w} \cdot \mathbf {x} _{i}-b\leq -1\qquad {\text{ for }}\mathbf {x} _{i}$ 属于第二类。

这可以改写为

$c_{i}(\mathbf {w} \cdot \mathbf {x} _{i}-b)\geq 1,\quad {\text{ for all }}1\leq i\leq n.\qquad \qquad (1)$

我们可以将这些组合起来得到优化问题

最小化（在 ${\mathbf {w} ,b}$ 中）

$\|\mathbf {w} \|$

受限于（对于任何 $i=1,\dots ,n$)

$c_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1.\,$

有偏超平面和无偏超平面

为了简单起见，有时需要超平面通过坐标系的原点。这种超平面被称为无偏，而一般不一定要通过原点的超平面被称为有偏。可以通过将 $b=0$ 设置为原始优化问题中的约束条件，强制执行无偏超平面。对应的对偶与上面给出的对偶相同，只是没有等式约束条件

$\sum _{i=1}^{n}\alpha _{i}c_{i}=0.$

转导支持向量机

转导支持向量机扩展了 SVM，因为它也可以在半监督学习中处理部分标记数据。在这里，除了训练集 ${\mathcal {D}}$ 之外，学习器还会获得一个集合

${\mathcal {D}}^{\star }=\{\mathbf {x} _{i}^{\star }|\mathbf {x} _{i}^{\star }\in \mathbb {R} ^{p}\}_{i=1}^{k}\,$

用于分类测试示例。形式上，转导支持向量机由以下原始优化问题定义

最小化（在 ${\mathbf {w} ,b,\mathbf {c^{\star }} }$ 中）

${\frac {1}{2}}\|\mathbf {w} \|^{2}$

受限于（对于任何 $i=1,\dots ,n$ 和任何 $j=1,\dots ,k$)

$c_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1,\,$

$c_{j}^{\star }(\mathbf {w} \cdot \mathbf {x_{j}^{\star }} -b)\geq 1,$

和

$c_{j}^{\star }\in \{-1,1\}.\,$

转导支持向量机是由弗拉基米尔·瓦普尼克在1998年提出的。

特性

SVM属于广义线性分类器家族。它们也可以被认为是Tikhonov正则化的特例。一个特殊的属性是，它们同时最小化经验 *分类误差* 并最大化 *几何裕度*；因此它们也被称为 *最大裕度分类器*。

迈耶、莱希和霍尼克对SVM与其他分类器的比较进行了研究。

线性SVM的扩展

软间隔

1995年，科琳娜·科特斯和弗拉基米尔·瓦普尼克提出了一种修正后的最大间隔思想，允许存在错误标记的样本。 如果不存在可以将“是”和“否”样本分开的超平面，则 *软间隔* 方法将选择一个尽可能干净地划分样本的超平面，同时仍然最大化与最近的干净划分样本的距离。该方法引入了松弛变量，$\xi _{i}$，它们衡量数据点 $x_{i}$ 的错误分类程度。

$c_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1-\xi _{i}\quad 1\leq i\leq n.\quad \quad (2)$

然后，目标函数通过一个惩罚非零 $\xi _{i}$ 的函数而增加，优化过程成为在较大裕度和较小误差惩罚之间的权衡。如果惩罚函数是线性的，则优化问题变为

$\min _{\mathbf {w} ,\mathbf {\xi } }\left\{{\frac {1}{2}}\|\mathbf {w} \|^{2}+C\sum _{i=1}^{n}\xi _{i}\right\}$

受限于 (对于任何 $i=1,\dots n$)

$c_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)\geq 1-\xi _{i},~~~~\xi _{i}\geq 0.$

这种在 (2) 中的约束以及最小化 $\|\mathbf {w} \|$ 的目标可以使用拉格朗日乘子解决，如上所述。然后，需要解决以下问题：

$\min _{\mathbf {w} ,\mathbf {\xi } ,b}\max _{{\boldsymbol {\alpha }},{\boldsymbol {\beta }}}\left\{{\frac {1}{2}}\|\mathbf {w} \|^{2}+C\sum _{i=1}^{n}\xi _{i}-\sum _{i=1}^{n}{\alpha _{i}[c_{i}(\mathbf {w} \cdot \mathbf {x_{i}} -b)-1+\xi _{i}]}-\sum _{i=1}^{n}\beta _{i}\xi _{i}\right\}$

其中 $\alpha _{i},\beta _{i}\geq 0$.

线性惩罚函数的主要优势在于松弛变量从对偶问题中消失，常数 *C* 仅作为拉格朗日乘子的额外约束出现。对于上述公式及其在实践中的巨大影响，Corinna Cortes|Cortes 和 Vladimir Vapnik|Vapnik 获得了 2008 年巴黎卡内拉基斯奖|ACM 巴黎卡内拉基斯奖 。非线性惩罚函数已被使用，特别是在减少异常值对分类器影响方面，但除非谨慎处理，否则问题会变得非凸，因此找到全局解决方案要困难得多。

非线性分类

弗拉基米尔·瓦普尼克在 1963 年提出的最初最佳超平面算法是一种线性分类器。然而，在 1992 年，伯恩哈德·博瑟、伊莎贝尔·吉永和瓦普尼克提出了一种方法，通过将核技巧（最初由 Aizerman 等人提出） 应用于最大间隔超平面来创建非线性分类器。 结果算法在形式上类似，只是每个点积都被非线性核（积分算子）|核函数替换。这使得算法能够在转换后的特征空间中拟合最大间隔超平面。变换可能是非线性的，转换后的空间可能是高维的；因此，尽管分类器在高维特征空间中是超平面，但它在原始输入空间中可能是非线性的。

如果使用的核是高斯径向基函数，也称为 RBF，则相应的特征空间是无限维的希尔伯特空间。最大间隔分类器是良好正则化的，因此无限维不会破坏结果。一些常见的内核包括：

• 齐次多项式|多项式（齐次）： $k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=(\mathbf {x_{i}} \cdot \mathbf {x_{j}} )^{d}$
• 多项式（非齐次）： $k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=(\mathbf {x_{i}} \cdot \mathbf {x_{j}} +1)^{d}$
• 高斯或径向基函数： $k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=\exp(-\gamma \|\mathbf {x_{i}} -\mathbf {x_{j}} \|^{2})$，对于 $\gamma >0$。有时使用 $\gamma =1/{2\sigma ^{2}}$ 参数化。
• 双曲函数|双曲正切：$k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=\tanh(\kappa \mathbf {x_{i}} \cdot \mathbf {x_{j}} +c)$，对于某些（并非所有）$\kappa >0$ 和 $c<0$

核函数与变换 $\varphi (\mathbf {x_{i}} )$ 通过以下等式相关联 $k(\mathbf {x_{i}} ,\mathbf {x_{j}} )=\varphi (\mathbf {x_{i}} )\cdot \varphi (\mathbf {x_{j}} )$。w 的值也在变换空间中，其中 $\textstyle \mathbf {w} =\sum _{i}\alpha _{i}c_{i}\varphi (\mathbf {x} _{i}).$。用于分类的 w 的点积可以通过核技巧计算，即 $\textstyle \mathbf {w} \cdot \varphi (\mathbf {x} )=\sum _{i}\alpha _{i}c_{i}k(\mathbf {x} _{i},\mathbf {x} )$。然而，一般情况下不存在一个值 w' 使得 $\mathbf {w} \cdot \varphi (\mathbf {x} )=k(\mathbf {w'} ,\mathbf {x} ).$

参数选择

SVM 的有效性取决于核函数、核函数的参数和软间隔参数 C 的选择。

一个常见的选择是高斯核函数，它只有一个参数 ?。C 和 ? 的最佳组合通常通过网格搜索选择，网格搜索使用指数增长的 C 和 ? 序列，例如，$C\in \{2^{-5},2^{-3},\dots ,2^{13},2^{15}\}$； $\gamma \in \{2^{-15},2^{-13},\dots ,2^{1},2^{3}\}$。每一对参数使用交叉验证进行检查，选择具有最佳交叉验证准确率的参数。最终模型用于测试和对新数据进行分类，它在整个训练集上使用所选参数进行训练。

问题

SVM 的潜在缺点如下两个方面：

• 未校准的类成员概率
• SVM 仅直接适用于两类任务。因此，必须应用将多类任务简化为多个二元问题的算法，参见多类 SVM 部分。

多类 SVM

多类别 SVM 旨在利用支持向量机为实例分配标签，其中标签来自一个包含多个元素的有限集合。最常用的方法是将单个多类别问题简化为多个二元分类问题。每个问题都会产生一个二元分类器，该分类器被认为会产生一个输出函数，该函数对来自正类的示例产生相对较大的值，而对来自负类的示例产生相对较小的值。构建此类二元分类器的两种常用方法是：每个分类器区分（i）一个标签与其余标签（一对多），或（ii）每个类别对之间（一对一）。对于一对多情况，新实例的分类通过赢家通吃策略完成，即输出函数值最高的分类器分配类别（重要的是，输出函数要经过校准以产生可比较的分数）。对于一对一方法，分类通过最大赢家投票策略完成，即每个分类器将实例分配到两个类别之一，然后分配类别的投票增加一票，最后票数最多的类别决定实例的分类。

结构化 SVM

SVM 已被推广到结构化 SVM，其中标签空间是结构化的，并且可能具有无限大小。

回归

1996 年，弗拉基米尔·瓦普尼克、哈里斯·德鲁克、克里斯·伯吉斯、琳达·考夫曼和亚历克斯·斯莫拉提出了 SVM 用于回归分析|回归的一个版本。^[8] 这种方法被称为支持向量回归 (SVR)。支持向量分类（如上所述）产生的模型仅取决于训练数据的子集，因为构建模型的成本函数并不关心超出边界的训练点。类似地，SVR 产生的模型仅取决于训练数据的子集，因为构建模型的成本函数会忽略任何靠近模型预测（在阈值 $\epsilon$ 内）的训练数据。支持向量机 (SVM) 还存在一个最小二乘版本，称为最小二乘支持向量机 (LS-SVM)，由 Suykens 和 Vandewalle 提出。^[9]

实现

最大边距超平面的参数是通过求解优化问题得到的。存在几种专门的算法可以快速求解 SVM 产生的 QP 问题，这些算法主要依赖于启发式方法将问题分解为更小、更易于管理的块。求解 QP 问题的常用方法是 Platt 的 序列最小优化 (SMO) 算法，该算法将问题分解为可以解析求解的二维子问题，从而无需数值优化算法。

另一种方法是使用内点法，该方法使用牛顿迭代法来找到原始问题和对偶问题 Karush-Kuhn-Tucker 条件的解。^[10] 这种方法不是求解一系列分解问题，而是直接将问题作为一个整体求解。为了避免求解涉及大型内核矩阵的线性系统，通常会使用该矩阵的低秩近似来使用内核技巧。

SVM 平台

目前存在多个数据科学平台，提供 SVM 算法的实现、训练、验证和测试。以下是一些例子

• Anaconda (Python 2.7, 3.5) (scikit learn)
• Matlab (统计和机器学习工具箱)

外部链接

• 支持向量机在模式识别中的教程 由 Christopher J. C. Burges 撰写。数据挖掘与知识发现 2:121–167, 1998
• www.kernel-machines.org (一般信息和研究论文集)
• www.support-vector-machines.org (支持向量机相关文献、综述、软件、链接 - 学术网站)
• videolectures.net (SVM 相关视频讲座)
• 动画剪辑: 使用多项式核的 SVM 可视化。
• Tristan Fletcher 为完全初学者提供的非常基础的 SVM 教程 [1].
• svmtutorial.online 对 SVM 的简单介绍，任何具有基本数学背景的人都可以轻松理解
• www.shogun-toolbox.org (Shogun (工具箱) 包含大约 20 种不同的 SVM 实现)
• libsvm libsvm 是一个积极修补的 SVM 库
• liblinear liblinear 是一个用于大型线性分类的库，包括一些 SVM
• flssvm flssvm 是一个用 fortran 编写的最小二乘 SVM 实现
• Shark Shark 是一个 C++ 机器学习库，实现了各种类型的 SVM
• dlib dlib 是一个 C++ 库，用于处理核方法和 SVM

参考文献

• Sergios Theodoridis 和 Konstantinos Koutroumbas "模式识别", 第 4 版, Academic Press, 2009.
• Nello Cristianini 和 John Shawe-Taylor. 支持向量机和其他基于核的学习方法介绍. 剑桥大学出版社, 2000. ISBN 0-521-78019-5 ([2] SVM 书籍)
• Huang T.-M., Kecman V., Kopriva I. (2006), 用于挖掘海量数据集的基于核的算法，监督、半监督和无监督学习，Springer-Verlag，柏林，海德堡，260 页。96 幅插图，精装，ISBN 3-540-31681-7 [3]
• Vojislav Kecman: "学习与软计算 - 支持向量机、神经网络、模糊逻辑系统", 麻省理工学院出版社，剑桥，马萨诸塞州，2001.[4]
• Bernhard Schölkopf 和 A. J. Smola: 用核学习. 麻省理工学院出版社，剑桥，马萨诸塞州，2002. (部分在线提供: [5].) ISBN 0-262-19475-9
• Bernhard Schölkopf, Christopher J.C. Burges 和 Alexander J. Smola (编辑)。"核方法进展: 支持向量学习". 麻省理工学院出版社，剑桥，马萨诸塞州，1999. ISBN 0-262-19416-3. [6]
• John Shawe-Taylor 和 Nello Cristianini. 用于模式分析的核方法. 剑桥大学出版社，2004. ISBN 0-521-81397-2 ([7] 核方法书籍)
• Ingo Steinwart 和 Andreas Christmann. 支持向量机. Springer-Verlag，纽约，2008. ISBN 978-0-387-77241-7 ([8] SVM 书籍)
• P.J. Tan 和 D.L. Dowe (2004), 斜决策树的 MML 推断, 人工智能讲义 (LNAI) 3339, Springer-Verlag, pp1082-1088. (本文使用最小消息长度 (最小消息长度|MML) 并且实际上将概率支持向量机整合到决策树学习|决策树的叶子中)。
• Vladimir Vapnik. 统计学习理论的本质. Springer-Verlag, 1995. ISBN 0-387-98780-0
• Vladimir Vapnik, S.Kotz "基于经验数据的依赖估计" Springer, 2006. ISBN 0387308652, 510 页 [这是 Vapnik 早期书籍的转载，描述了 SVM 方法背后的理念。2006 年的附录描述了最近的发展]。
• Dmitriy Fradkin 和 Ilya Muchnik "用于分类的支持向量机" 在 J. Abello 和 G. Carmode (编) "流行病学中的离散方法" 中，DIMACS 离散数学与理论计算机科学丛书，第 70 卷，第 13-20 页，2006. [9]. 简洁地描述了 SVM 背后的理论思想。
• Kristin P. Bennett 和 Colin Campbell, "支持向量机: 炒作还是赞歌?", SIGKDD 探索, 2,2, 2000, 1-13. [10]. 对 SVM 的出色介绍，包含有用的图表。
• Ovidiu Ivanciuc, "支持向量机在化学中的应用", 在: 计算化学评论, 第 23 卷, 2007, 第 291-400 页. 可转载: [11]
• Catanzaro, Sundaram, Keutzer, "图形处理器上的快速支持向量机训练和分类", 在: 国际机器学习大会, 2008 [12]