量子世界/附录/微积分

微积分：一个非常简短的介绍

另一种方法，我们可以从无穷小的量中获得一个定义明确的有限数，就是将一个这样的量除以另一个量。

我们将在整个过程中假设我们正在处理行为良好的函数，这意味着你可以绘制这样的函数的图形而不抬起你的铅笔，并且你也可以对函数的每个导数做同样的事情。那么什么是函数，什么是函数的导数呢？

一个函数 $f(x)$ 是一个带有输入和输出的机器。输入一个数字 $x$ ，就会输出数字 $f(x).$ 有点令人困惑的是，我们有时将 $f(x)$ 不仅仅看作一个输出数字的机器，而是看作当插入 $x$ 时输出的数字。

（第一个）导数 $f'(x)$ 的 $f(x)$ 是一个函数，它告诉我们 $f(x)$ 在 $x$ 增加时（从给定值开始 $x,$ 比如 $x_{0}$ ) 增加多少，在 $x$ 的增加量 $\Delta x$ 和 $f(x)$ 的对应增加量 $\Delta f=f(x+\Delta x)-f(x)$ （当然可能为负）趋于 0

f'(x_{0})=\lim _{\Delta x\rightarrow 0}{\Delta f \over \Delta x}={df \over dx}(x_{0}).

上面的图表说明了这个极限。比值 $\Delta f/\Delta x$ 是穿过黑点的直线的斜率（即 $\tan$ 正 $x$ 轴与直线之间的夹角，从正 $x$ 轴逆时针方向测量）。当 $\Delta x$ 减小，位于 $x+\Delta x$ 的黑点沿着 $f(x)$ 的图形滑向位于 $x,$ 的黑点，而直线的斜率增大。在极限 $\Delta x\rightarrow 0,$ 时，直线成为 $f(x),$ 的切线，在 $x.$ 与其相切。 $f(x)$ 在 $x_{0}$ 处的切线的斜率就是我们所说的 $f(x)$ 在 $x_{0}.$

所以，函数 $f(x)$ 的一阶导数 $f'(x)$ 是一个函数，它对于每个 $x.$ 都等于 $f(x)$ 的斜率。求导一个函数 $f$ 就是求得它的一阶导数 $f'.$ 对 $f',$ 求导，我们得到 $f,$ 的二阶导数 $f''={\frac {d^{2}f}{dx^{2}}}$ ，对 $f''$ 求导，我们得到三阶导数 $f'''={\frac {d^{3}f}{dx^{3}}},$ 等等。

很容易证明，如果 $a$ 是一个数字，并且 $f$ 和 $g$ 是 $x,$ 的函数，则

{d(af) \over dx}=a{df \over dx}

和

{d(f+g) \over dx}={df \over dx}+{dg \over dx}.

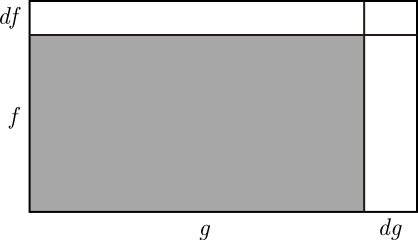
一个稍微难一点的问题是，求两个关于 $x.$ 的函数的乘积 $e=fg$ 的导数。将 $f$ 和 $g$ 视为面积为 $e.$ 的矩形的垂直边和水平边。当 $x$ 增加 $\Delta x,$ 乘积 $fg$ 增加图中三个白色矩形的面积之和。

换句话说，

\Delta e=f(\Delta g)+(\Delta f)g+(\Delta f)(\Delta g)

因此

{\frac {\Delta e}{\Delta x}}=f\,{\frac {\Delta g}{\Delta x}}+{\frac {\Delta f}{\Delta x}}\,g+{\frac {\Delta f\,\Delta g}{\Delta x}}.

如果我们现在取极限，其中 $\Delta x$ 以及因此 $\Delta f$ 和 $\Delta g$ 趋近于 0，则右手边的前两项趋近于 $fg'+f'g.$ 第三项怎么样？因为它是一个趋近于 0 的表达式（ $\Delta f$ 或 $\Delta g$ ）与一个趋近于有限值的表达式（ $\Delta g/\Delta x$ 或 $\Delta f/\Delta x$ ）的乘积，因此它趋近于 0。底线

e'=(fg)'=fg'+f'g.

这很容易推广到 $n$ 个函数的乘积。这是一个特例

(f^{n})'=f^{n-1}\,f'+f^{n-2}\,f'\,f+f^{n-3}\,f'\,f^{2}+\cdots +f'\,f^{n-1}=n\,f^{n-1}f'.

观察到，两个等号之间有 $n$ 个相等的项。如果函数 $f$ 返回你插入的任何东西，这归结为

(x^{n})'=n\,x^{n-1}.

现在假设 $g$ 是 $f$ 的函数，而 $f$ 是 $x.$ 的函数。当 $x$ 增加 $\Delta x$ 时， $f$ 增加 $\Delta f\approx {\frac {df}{dx}}\Delta x,$ 这反过来会导致 $g$ 增加 $\Delta g\approx {\frac {dg}{df}}\Delta f.$ 因此 ${\frac {\Delta g}{\Delta x}}\approx {\frac {dg}{df}}{\frac {df}{dx}}.$ 在极限 $\Delta x\rightarrow 0$ 时， $\approx$ 变为 $=$