想象一个物体 ,它可以自由地在单一维度运动 - 例如,沿着
,它可以自由地在单一维度运动 - 例如,沿着 轴。就像任何物理物体一样,它具有或多或少的模糊位置(相对于我们选择的任何参考物体)。为了描述它的模糊位置,量子力学为我们提供了概率密度
轴。就像任何物理物体一样,它具有或多或少的模糊位置(相对于我们选择的任何参考物体)。为了描述它的模糊位置,量子力学为我们提供了概率密度  这取决于实际的测量结果,它允许我们计算在
这取决于实际的测量结果,它允许我们计算在 轴的任何给定区间内找到粒子的概率,前提是进行了适当的测量。(记住我们的口号:量子力学的数学形式主义是为了根据实际结果为可能的测量结果分配概率。)
轴的任何给定区间内找到粒子的概率,前提是进行了适当的测量。(记住我们的口号:量子力学的数学形式主义是为了根据实际结果为可能的测量结果分配概率。)
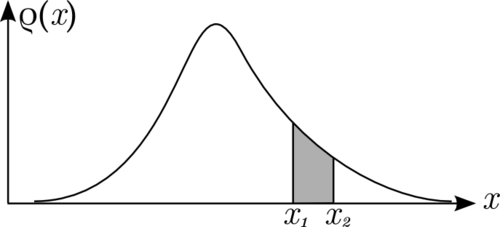
我们称 为概率密度,因为它表示每单位长度的概率。在
为概率密度,因为它表示每单位长度的概率。在 和
和  之间的区间内找到
之间的区间内找到 的概率由
的概率由 的图形、
的图形、 轴以及在
轴以及在 和
和  处的垂直线之间的面积
处的垂直线之间的面积  所给出。我们如何计算这个面积?诀窍是用宽度为
所给出。我们如何计算这个面积?诀窍是用宽度为 的窄矩形覆盖它。
的窄矩形覆盖它。

左侧第一个矩形的面积为  ,第二个矩形的面积为
,第二个矩形的面积为  ,最后一个矩形的面积为
,最后一个矩形的面积为  这些面积的总和可以用简写符号表示为
这些面积的总和可以用简写符号表示为

不难想象,如果我们增加矩形数量  ,同时减小每个矩形的宽度
,同时减小每个矩形的宽度  ,那么所有这些矩形的面积总和,都将越来越逼近
,那么所有这些矩形的面积总和,都将越来越逼近  在
在  和
和  之间曲线下的面积
之间曲线下的面积  ,从而越来越逼近找到
,从而越来越逼近找到  在
在  和
和  当
当  趋于 0 且
趋于 0 且  趋于无穷大 (
趋于无穷大 ( ) 时,上面的求和式将趋于积分
) 时,上面的求和式将趋于积分

有时我们将此称为定积分,以强调它只是一个数字。(正如你所料,也有不定积分,你将在后面学习更多关于它们的内容。)大写 Δ 已变成一个  ,表明
,表明  是一个无限小的(或无穷小)宽度,求和符号(大写 Σ)已变成一个拉长的 S,表示我们正在添加无限多个无穷小面积。
是一个无限小的(或无穷小)宽度,求和符号(大写 Σ)已变成一个拉长的 S,表示我们正在添加无限多个无穷小面积。
不要让“无穷小”这个词吓到你。一个无穷小量本身没有意义。它是组合了积分符号  和无穷小量
和无穷小量  ,它作为极限是有意义的,其中
,它作为极限是有意义的,其中  超过任何大数字,
超过任何大数字, (因此每个矩形的面积)缩小到任何(正)数字以下,无论它多么小,而面积之和趋向于一个明确定义的有限数字。
(因此每个矩形的面积)缩小到任何(正)数字以下,无论它多么小,而面积之和趋向于一个明确定义的有限数字。
























