量子世界/附录/相对论/洛伦兹收缩时间膨胀

洛伦兹收缩，时间膨胀

想象一根静止在 ${\mathcal {F}}'.$ 中的米尺。在时间 $t'=0,$，它的两端位于点 $O$ 和 $C.$ 在时间 $t=0,$ 它们位于点 $O$ 和 $A,$ 这两点之间的距离小于一米。现在想象一根静止在 ${\mathcal {F}},$ 中的棍子（不是米尺），它的两端在时间 $t'=0$ 位于 O 和 C。在 ${\mathcal {F}}'$ 中它们之间距离一米，但在棍子的静止系中它们位于点 $O$ 和 $B$，因此距离超过一米。底线：运动物体在运动方向上会收缩（缩短）。

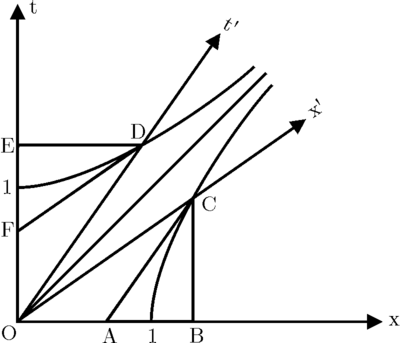
接下来想象两个时钟，一个 (${\mathcal {C}}$) 在 ${\mathcal {F}}$ 中静止，位于 $x=0,$ 另一个 (${\mathcal {C}}'$) 在 ${\mathcal {F}}'$ 中静止，位于 $x'=0.$ 在 $D,$ ${\mathcal {C}}'$ 表明已经过去了1秒，而在 $E$（在 ${\mathcal {F}}$ 中与 $D$ 同时发生），${\mathcal {C}}$ 表明已经过去了超过1秒。另一方面，在 $F$（在 ${\mathcal {F}}'$ 中与 $D$ 同时发生），${\mathcal {C}}$ 表明已经过去了不到1秒。结论是：运动的时钟比静止的时钟走得慢。

例如：μ子 ($\mu$ 粒子) 在大气层顶部附近产生，大约在10公里处，当来自宇宙的高能粒子撞击大气层时。由于μ子自发衰变，平均寿命为2.2微秒，因此它们的行进距离不超过600米。然而，许多μ子被发现到达海平面。它们是如何到达那里的呢？

答案在于，大多数μ子以接近光速的速度运动。从μ子自身的角度来看（即相对于它处于静止状态的惯性系），μ子的寿命只有大约2微秒；但从我们的角度来看（即相对于一个惯性系，其中μ子以接近光速的速度运动），μ子的寿命要长得多，有足够的时间到达地球表面。