量子世界/附录/向量

向量（空间）

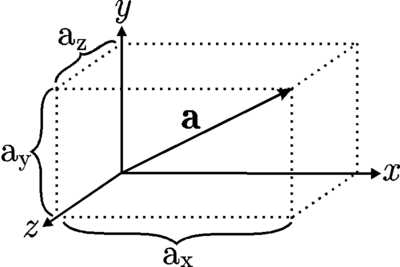
一个 向量 是既有大小又有方向的量。向量可以被可视化为箭头。下图展示了我们对向量 $\mathbf {a} .$ 的分量 $(a_{x},a_{y},a_{z})$ 的理解。

两个向量的和 $\mathbf {a} +\mathbf {b}$ 的分量为 $(a_{x}+b_{x},a_{y}+b_{y},a_{z}+b_{z}).$

• 用箭头解释向量的加法。

两个向量的 点积 是一个数

$\mathbf {a} \cdot \mathbf {b} =a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}.$

它的重要性在于它在 旋转 下是不变的。为了证明这一点，我们计算

$(\mathbf {a} +\mathbf {b} )\cdot (\mathbf {a} +\mathbf {b} )=(a_{x}+b_{x})^{2}+(a_{y}+b_{y})^{2}+(a_{z}+b_{z})^{2}=$

$a_{x}^{2}+a_{y}^{2}+a_{z}^{2}+b_{x}^{2}+b_{y}^{2}+b_{z}^{2}+2\,(a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z})=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} +2\,\mathbf {a} \cdot \mathbf {b} .$

根据毕达哥拉斯定理，$\mathbf {a}$ 的大小为 $a={\sqrt {a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}.$ 如果我们使用不同的坐标系，$\mathbf {a}$ 的分量将不同：$(a_{x},a_{y},a_{z})\rightarrow (a'_{x},a'_{y},a'_{z}).$ 但是如果新的坐标系仅仅是通过旋转和/或平移得到的，$\mathbf {a}$ 的大小将保持不变

${\sqrt {a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}={\sqrt {(a'_{x})^{2}+(a'_{y})^{2}+(a'_{z})^{2}}}.$

平方的大小 $\mathbf {a} \cdot \mathbf {a} ,$ $\mathbf {b} \cdot \mathbf {b} ,$ 和 $(\mathbf {a} +\mathbf {b} )\cdot (\mathbf {a} +\mathbf {b} )$ 在旋转下是不变的，因此，乘积 $\mathbf {a} \cdot \mathbf {b} .$

• 证明点积在平移下也是不变的。

由于标量是指在某些变换下（在本例中为坐标轴的旋转和/或平移）保持不变的数字，因此点积也被称为（a）标量积。我们来证明

$\mathbf {a} \cdot \mathbf {b} =ab\cos \theta ,$

其中 $\theta$ 是 $\mathbf {a}$ 和 $\mathbf {b} .$ 之间的夹角。为此，我们选择一个坐标系 ${\mathcal {F}}$，其中 $\mathbf {a} =(a,0,0).$ 在此坐标系中，$\mathbf {a} \cdot \mathbf {b} =ab_{x}$，其中 $b_{x}=b\cos \theta .$ 由于 $\mathbf {a} \cdot \mathbf {b}$ 是一个标量，并且标量在旋转和平移下是不变的，所以结果 $\mathbf {a} \cdot \mathbf {b} =ab\cos \theta$（不依赖于任何特定框架）在相对于 ${\mathcal {F}}.$ 旋转和平移的所有框架中都成立。

现在我们引入单位向量 $\mathbf {\hat {x}} ,\mathbf {\hat {y}} ,\mathbf {\hat {z}} ,$，它们的指向由坐标轴定义。它们被称为构成一个正交规范基。正交是因为它们彼此正交

$\mathbf {\hat {x}} \cdot \mathbf {\hat {y}} =\mathbf {\hat {x}} \cdot \mathbf {\hat {z}} =\mathbf {\hat {y}} \cdot \mathbf {\hat {z}} =0.$

规范是因为它们是单位向量

$\mathbf {\hat {x}} \cdot \mathbf {\hat {x}} =\mathbf {\hat {y}} \cdot \mathbf {\hat {y}} =\mathbf {\hat {z}} \cdot \mathbf {\hat {z}} =1.$

它们是“**正交的**”，因为它们是相互垂直的；它们也是“**标准化的**”，因为它们的大小都是 1。 而它们被称作“**基**”是因为每一个向量 $\mathbf {v}$ 都可以被写成这三个向量的 线性组合 —— 也就是说，一个每个基向量出现一次的求和，并乘以 $\mathbf {v}$ 的对应分量（该分量可以是 0）

$\mathbf {v} =v_{x}\mathbf {\hat {x}} +v_{y}\mathbf {\hat {y}} +v_{z}\mathbf {\hat {z}} .$

可以很容易地看出 $v_{x}=\mathbf {\hat {x}} \cdot \mathbf {v} ,$ $v_{y}=\mathbf {\hat {y}} \cdot \mathbf {v} ,$ $v_{z}=\mathbf {\hat {z}} \cdot \mathbf {v} ,$ 这就是我们有以下结论的原因

$\mathbf {v} =\mathbf {\hat {x}} \,(\mathbf {\hat {x}} \cdot \mathbf {v} )+\mathbf {\hat {y}} \,(\mathbf {\hat {y}} \cdot \mathbf {v} )+\mathbf {\hat {z}} \,(\mathbf {\hat {z}} \cdot \mathbf {v} ).$

另一个有用的定义（尽管只适用于 3 维空间）是两个向量的 叉积

$\mathbf {a} \times \mathbf {b} =(a_{y}b_{z}-a_{z}b_{y})\,\mathbf {\hat {x}} +(a_{z}b_{x}-a_{x}b_{z})\,\mathbf {\hat {y}} +(a_{x}b_{y}-a_{y}b_{x})\,\mathbf {\hat {z}} .$

• 证明叉积是反对称的：$\mathbf {a} \times \mathbf {b} =-\mathbf {b} \times \mathbf {a} .$

因此，$\mathbf {a} \times \mathbf {a} =0.$

• 证明$\mathbf {a} \cdot (\mathbf {a} \times \mathbf {b} )=\mathbf {b} \cdot (\mathbf {a} \times \mathbf {b} )=0.$

因此$\mathbf {a} \times \mathbf {b}$ 与$\mathbf {a}$ 和 $\mathbf {b} .$ 垂直。

• 证明$\mathbf {a} \times \mathbf {b}$ 的大小等于 $ab\sin \alpha ,$ 其中 $\alpha$ 是$\mathbf {a}$ 和 $\mathbf {b} .$ 之间的夹角。提示：使用一个坐标系，其中 $\mathbf {a} =(a,0,0)$ 且 $\mathbf {b} =(b\cos \alpha ,b\sin \alpha ,0).$

因为 $ab\sin \alpha$ 也是平行四边形 $P$ 的面积 $A$，我们可以将 $\mathbf {a} \times \mathbf {b}$ 看作一个大小为 $A$ 的向量，它垂直于 $P.$ 由于叉积产生一个向量，它也被称为向量积。

（我们省去了证明叉积在坐标轴平移和旋转下是不变的，这是向量所必需的。但是，让我们顺便提一下，如果 $\mathbf {a}$ 和 $\mathbf {b}$ 是极向量，那么 $\mathbf {a} \times \mathbf {b}$ 是一个轴向量。在反射（例如，坐标轴的反转）下，一个普通（或极性）向量是不变的，而一个轴向量改变了它的符号。）

这里有一个涉及标量积和向量积的实用关系

$\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {c} \cdot \mathbf {a} )-(\mathbf {a} \cdot \mathbf {b} )\mathbf {c} .$