原子

原子看起来像什么？

像这样？

还是像这样？

$\rho _{2p0}$
$\rho _{3p0}$
$\rho _{3d0}$
$\rho _{4p0}$
$\rho _{4d0}$
$\rho _{4f0}$
$\rho _{5d0}$
$\rho _{5f0}$

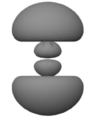
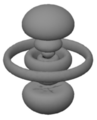
这些图像都没有描述真实的原子。这是因为我们甚至无法真实地可视化原子。虽然你可以尝试将第一行中的图像从你的记忆中抹去——它们代表了一种看待原子的方式，这种方式过于简化，不适合我们想要开始思考的方式——但下一行中的八个模糊图像值得仔细研究。每个图像都代表了氢原子的静止态的一个方面。你既无法感知原子核（一个质子），也无法感知电子。你所看到的是一个模糊的位置。更准确地说，你所看到的是云状的模糊，它们关于垂直和水平轴对称，并且代表了原子的内部相对位置——电子相对于质子的位置或质子相对于电子的位置。

原子的状态是什么？
什么是静止态？
模糊的位置到底是什么？
这种模糊是如何代表原子的内部相对位置的？
为什么我们不能真实地描述原子的内部相对位置？

量子态

在量子力学中，态是概率算法。我们使用它们根据实际测量结果来计算对测量的可能结果的概率。量子态将其输入作为

一个或多个测量结果，
一个测量 M，
M 的时间，

它将其输出作为 M 的可能结果的概率。

如果量子态所分配的概率独立于测量时间，则称其为静止态。

从数学的角度来看，每个模糊图代表一个密度函数 $\rho ({\boldsymbol {r}})$ 。想象一个小的区域 $R$ ，就像第一个模糊图中的小方块。假设这是一个相对于质子的位置（数学）空间的区域。如果你在 $R$ 上对 $\rho ({\boldsymbol {r}})$ 进行积分，你将得到找到电子在 $R$ 中的概率 $p\,(R)$ ，前提是进行了适当的测量。

p\,(R)=\int _{R}\rho ({\boldsymbol {r}})\,d^{3}{\boldsymbol {r}}.

这里“适当”是指能够确定命题“电子在 $R$ 中”的真值，可能的真值为“真”或“假”。我们在以下每个图像中看到的是一个恒定概率密度的表面。

$\rho _{2p0}$
$\rho _{3p0}$
$\rho _{3d0}$
$\rho _{4p0}$
$\rho _{4d0}$
$\rho _{4f0}$
$\rho _{5d0}$
$\rho _{5f0}$

现在想象一下进行了适当的测量。在测量之前，电子既不在 $R$ 内也不在 $R$ 外。如果它在里面，那么在外面找到它的概率为零；如果它在外面，那么在里面找到它的概率为零。在测量之后，另一方面，电子要么在 $R$ 内，要么在 $R$ 外。

结论

在测量之前，命题“电子在 $R$ 中”既不是真也不是假；它缺乏一个（确定的）真值。
测量通常会改变其作用的系统的状态。

如前所述，概率不仅分配给测量结果，而且基于测量结果。每个密度函数 $\rho _{nlm}$ 用于为测量电子相对于质子的位置的可能结果分配概率。在每种情况下，分配都基于对三个可观察量的同时测量的结果：原子的能量（由主量子数 $n$ 的值指定），其总角动量 $l$ （由一个字母指定，这里为p、d或f），以及其角动量的垂直分量 $m$ 。

模糊的可观察量

我们说一个可观察量 $Q$ 具有有限或可数的可能值 $q_{k}$ 是模糊的（或者说它具有模糊值）当且仅当至少有一个命题“ $Q$ 的值为 $q_{k}$ ” 缺乏真值。这等效于以下充要条件：分配给至少一个值 $q_{k}$ 的概率既不是 0 也不是 1。

那么对于通常被描述为连续的可观察量，比如位置，情况又如何呢？

将一个可观察量描述为“连续”可能具有误导性。一方面，我们不能将一个可观察量及其可能值与测量及其可能结果分离，而具有不可数个可能结果的测量在原则上也是不可能的。另一方面，不存在一个名为“位置”的单一可观察量。空间的不同划分定义了具有不同可能结果集的不同位置测量。

推论：位置测量的可能结果（或位置可观察量的可能值）由空间的划分定义。它们构成一个有限或可数的空间区域集合。因此，精确的位置既不是可能的测量结果，也不是位置可观察量的可能值。

那么这些云状模糊如何表示电子相对于质子的模糊位置呢？严格地说，它们以图形方式表示精确相对位置的数学空间中的概率密度，而不是模糊位置。正是这些概率密度通过允许我们计算每个位置可观察量的每个可能值的概率来表示模糊位置。

现在应该清楚为什么我们不能描述原子的内部相对位置本身。描述一个模糊的可观察量就是给测量可能的结果分配概率。但是，一个基于测量已完成的假设的描述，并没有描述一个可观察量本身（本身，无论测量与否）。

NEXT >