量子世界/附录/相对论/洛伦兹

反对 $K>0$ 的论据

在一个假设的世界中，$K>0$，我们可以定义 $k\equiv 1/{\sqrt {K}}$ （一个具有速度维度的普适常数），我们可以将 $u=v+w/(1-Kvw)$ 转化为以下形式

$u={v+w \over 1-vw/k^{2}}.$

If we plug in $v=w=k/2,$ then instead of the Galilean $u=v+w=k$ we have $u={4 \over 3}k>k.$ Worse, if we plug in $v=w=k,$ we obtain $u=\infty$: if object $O$ travels with speed $k$ relative to ${\mathcal {F}}_{2},$ and if ${\mathcal {F}}_{2}$ travels with speed $k$ relative to ${\mathcal {F}}_{1}$ (in the same direction), then $O$ travels with an infinite speed relative to ${\mathcal {F}}_{1}$! And if $O$ travels with $2k$ relative to ${\mathcal {F}}_{2}$ and ${\mathcal {F}}_{2}$ travels with $2k$ relative to ${\mathcal {F}}_{1},$ $O$'s speed relative to ${\mathcal {F}}_{1}$ is negative: $u=-{4 \over 3}k.$

如果我们使用 $K=k=1,$ 的单位，则与无穷小路径段相关的固有时间不变量与该路径段的惯性分量之间的关系为

$ds^{2}=dt^{2}+dx^{2}+dy^{2}+dz^{2}.$

这是 3 标量 $dx^{2}+dy^{2}+dz^{2},$ 的四维版本，该标量在空间旋转下是不变的。因此，如果 $K$ 为正，则惯性系之间的变换是时空中的旋转。我想你现在明白了为什么在这个假设的世界中，两个正速度的组合可以是一个负速度。

让我们通过从 $x'$ 和 $t'$ 轴相对于 $x$ 和 $t$ 轴是旋转的假设推导出组合定理（对于 $k{=}1$）来确认这一结论。

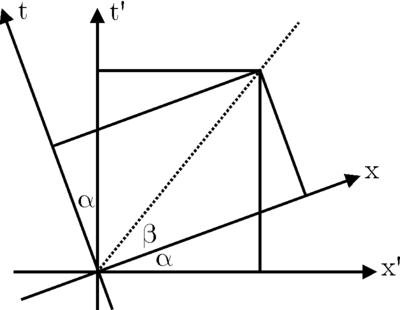
沿着虚线运动的物体 $O$ 相对于 ${\mathcal {F}}',$ 的速度为 $w=\cot(\alpha +ta)$，而 ${\mathcal {F}}'$ 相对于 ${\mathcal {F}}$ 的速度为 $v=\tan \alpha ,$ 同时 $O$ 相对于 ${\mathcal {F}}$ 的速度为 $u=\cot \beta .$ 利用三角关系

$\tan(\alpha +\beta )={\tan \alpha +\tan \beta \over 1-\tan \alpha \tan \beta },$

我们可以得出结论， ${1 \over w}={v+1/u \over 1-v/u}.$ 解出 $u,$ 得到 $u={v+w \over 1-vw}.$

我们如何排除 $K>0$ 的先验可能性？正如本书中所述，物质的稳定性——更准确地说，存在稳定的物体，这些物体 (i) 具有空间范围（它们“占据”空间），以及 (ii) 由有限数量没有空间范围的物体（它们不“占据”空间）构成——取决于相对位置的存在，这些位置是 (a) 或多或少模糊的，以及 (b) 与时间无关的。此类相对位置由概率分布描述，这些分布 (a) 在空间上是 *非均匀* 的，以及 (b) 在时间上是 *均匀* 的。因此，它们的客观存在需要时空的时间维度与空间维度之间存在客观差异。这排除了 $K>0.$ 的可能性。

为什么？如果 $K<0,$ 并且我们使用自然单位，其中 $c=1,$ 我们有

$ds^{2}=+\,dt^{2}-dx^{2}-dy^{2}-dz^{2}.$

从物理学的角度来看，$dt$ 前面的正号和 $dx,$ $dy,$ 和 $dz$ 前面的负号之间的唯一客观差异是时空中的时间和空间维度。如果 $K$ 为正，即使这种差异也不存在。

反对零 K 的论据

那么，什么论据反对 $K=0$ 的可能性呢？

回顾自由稳定粒子的传播子

$\langle B|A\rangle =\int {\mathcal {DC}}e^{-ibs[{\mathcal {C}}]}.$

如果 $K$ 为零，那么我们将有 $ds^{2}=dt^{2}.$ 惯性时间和固有时之间将没有区别，所有从 $A$ 到 $B$ 的时空路径都将对传播子 $\langle B|A\rangle ,$ 贡献相同的振幅 $e^{-ib(t_{B}-t_{A})}$，结果将是无望的发散。更糟糕的是，$\langle B|A\rangle$ 将与 $A$ 和 $B.$ 之间的距离无关。为了获得定义明确的有限概率，必须发生抵消（“相消干涉”），这排除了 $K=0.$

实际的洛伦兹变换

因此，在现实世界中，洛伦兹变换的形式为

$t'={t-wx/c^{2} \over {\sqrt {1-w^{2}/c^{2}}}},\quad x'={x-wt \over {\sqrt {1-w^{2}/c^{2}}}},\quad y'=y,\quad z'=z.$

让我们用自然单位（$c=1$）以图表方式对其进行探索。令 $t'=0,$ 我们得到 $t=wx.$ 这告诉我们 $x'$ 轴相对于未带撇号的坐标系的斜率是 $w=\tan \alpha .$ 令 $x'=0,$ 我们得到 $t=x/w.$ 这告诉我们 $t'$ 轴的斜率是 $1/w.$ 因此，带撇号的坐标轴以相同角度但以*相反*的方向旋转；如果 $t'$ 轴相对于 $t$ 轴顺时针旋转，那么 $x'$ 轴相对于 $x$ 轴逆时针旋转。

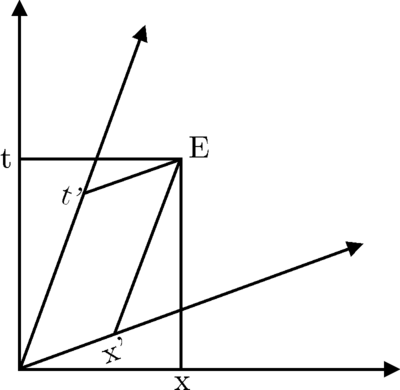
如果我们考虑运动中时钟的同步，我们将得出相同的结论。假设三个时钟（1、2、3）相对于 ${\mathcal {F}}.$ 以相同的速率 $w=\tan \alpha$ 运动。为了同步它们，我们必须从一个时钟向另一个时钟发送信号。什么类型的信号？如果我们希望我们的同步过程独立于我们使用的语言（即独立于参考系），那么我们必须使用以不变速率 $c.$ 传播的信号。

以下是它的工作原理

光信号从时钟 2（事件 $A$) 发送，并被时钟 1 和 3 反射（事件 $B$ 和 $C,$ 分别）。时钟之间的距离经过调整，使得反射信号同时到达时钟 2（事件 $D$）。这确保了时钟 1 和 2 之间的距离等于时钟 2 和 3 之间的距离，无论它们在哪个惯性系中进行比较。在 ${\mathcal {F}}',$ 时钟静止，来自 $A$ 的信号在分别到达第一个和第三个时钟时已经传播了相同的距离。由于它们还以相同的速度 $c,$ 传播，因此它们已经传播了相同的时间。因此，时钟必须同步，以便 $B$ 和 $C$ 是同时发生的。我们可以使用时钟 1 的世界线作为 $t'$ 轴，并且过 $B$ 和 $C$ 的直线作为 $x'$ 轴。很容易看到，上图中的三个角度 $ta$ 是相等的。根据这一点以及从 $B$ 到 $D$ 的信号的斜率等于 1（考虑到 $c{=}1$），两个角度 $\alpha$ 相等。

因此，同时性取决于我们用来描述物理情况的语言——惯性系。如果两个事件 $E_{1},E_{2}$ 在一个参考系中是同时发生的，那么在其他参考系中，$E_{1}$ 发生在 $E_{2}$ 之后，也存在参考系，$E_{1}$ 发生在 $E_{2}.$

我们在空间和时间轴上放置单位点在哪里？ ${\mathcal {F}}'$ 时间轴的单位点坐标为 $t'=1,x'=0$ 且满足 $t^{2}-x^{2}=1,$ 这可从 (\ref{ds2}) 的版本 $(t')^{2}-(x')^{2}=t^{2}-x^{2}$ 中得出。 $x'$ 轴的单位点坐标为 $t'=0,x'=1$ 且满足 $x^{2}-t^{2}=1.$ 空间和时间轴单位点的轨迹是由这些方程定义的双曲线。