这个量子世界/严重疾病/玻尔

玻尔

1913年，尼尔斯·玻尔假设轨道原子电子的角动量$L$是量子化的：“允许”的值是$\hbar$的整数倍。

$L=n\hbar$ 其中$n=1,2,3,\dots$

为什么量子化角动量，而不是任何其他量？

• 给定频率的辐射能量以普朗克常数的倍数量子化。
• 普朗克常数的单位与角动量相同。

玻尔的假设不仅解释了原子的稳定性，还解释了原子发射和吸收电磁辐射的原因是离散的。此外，它使他能够以惊人的精确度计算原子氢的光谱——原子氢能够发射和吸收光的频率（可见光以及红外线和紫外线）。下图显示了原子氢的可见发射光谱，其中包含巴尔默系的四条线。

原子氢的可见发射光谱，包含巴尔默系的四条线。

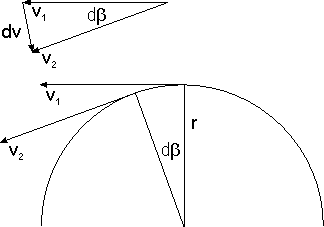
除了他的量子化假设外，玻尔在这一点上的推理仍然完全是经典的。让我们假设与玻尔一样，电子的轨道是半径为$r.$的圆。然后电子的速度由$v=r\,d\beta /dt,$给出，其加速度的大小由$a=dv/dt=v\,d\beta /dt.$给出。消除$d\beta /dt$得到$a=v^{2}/r.$ 在厘米-克-秒单位制中，库仑力的大小简化为$F=e^{2}/r^{2},$ 其中$e$是电子和质子电荷的大小。通过牛顿的$F=ma$，最后两个方程得到$m_{e}v^{2}=e^{2}/r,$ 其中$m_{e}$是电子的质量。如果我们将质子视为静止，则对于电子的动能，我们得到$T=m_{e}v^{2}/2=e^{2}/2r$。

如果将电子在无穷远处的势能设为 0，那么它在距离质子 $r$ 处的势能 $V$ 等于将其从 $r$ 移到无穷远所需的功的负值。

$V=-\int _{r}^{\infty }F(r')\,dr'=-\int _{r}^{\infty }\!{e^{2} \over (r')^{2}}\,dr'=+\left[{e^{2} \over r'}\right]_{r}^{\infty }=0-{e^{2} \over r}.$

因此，电子的总能量为

$E=T+V=e^{2}/2r-e^{2}/r=-e^{2}/2r.$

我们希望用电子的角动量 $L=m_{e}vr.$ 来表示它。记住 $m_{e}v^{2}=e^{2}/r,$，因此 $rm_{e}^{2}v^{2}=m_{e}e^{2},$，并将分子 $e^{2}\,$ 乘以 $m_{e}e^{2}$，分母 $2r$ 乘以 $rm_{e}^{2}v^{2},$ 我们得到

$E=-{e^{2} \over 2r}=-{m_{e}e^{4} \over 2m_{e}^{2}v^{2}r^{2}}=-{m_{e}e^{4} \over 2L^{2}}.$

现在，玻尔与经典物理学产生了分歧：他简单地用 $n\hbar$ 替换了 $L$。角动量的“允许”值定义了一系列原子能量的允许值。

$E_{n}=-{1 \over n^{2}}\left({m_{e}e^{4} \over 2\hbar ^{2}}\right),\quad n=1,2,3,\dots$

因此，原子只能以等于差值的绝对值的数量发射或吸收能量

$\Delta E_{nm}=E_{n}-E_{m}=\left({1 \over n^{2}}-{1 \over m^{2}}\right)\,{\hbox{Ry}},$

一个里德伯常数 (Ry) 等于 $m_{e}e^{4}/2\hbar ^{2}=13.6056923(12)\,{\hbox{eV.}}$ 这也是原子氢的电离能 $\Delta E_{1\infty }$——将电子从质子中完全移除所需的能量。 玻尔的预测值与测量值非常吻合。

使用上述原子能量的两个表达式并求解$r,$，我们得到$r=n^{2}\hbar ^{2}/m_{e}e^{2}.$ 对于基态$(n=1)$，这是氢原子的玻尔半径，等于$\hbar ^{2}/m_{e}e^{2}=5.291772108(18)\times 10^{-11}m.$ 成熟的理论得出了相同的数字，但将其解释为如果测量电子与质子的距离，则最有可能找到电子的质子距离。