运输地理与网络科学/弹性
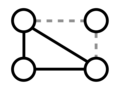
Sudakov 和 Vu (2008)[1]提出了图论中弹性的最具体定义:如果图 G 具有属性 P,那么需要移除多少条边才能使 G 不再具有 P?[2]例如,考虑图 1 及其关于连通性的弹性。移除任何一条边都会留下一个仍然连通的图。必须移除两条边才能生成一个不连通的图(图 2)。因此,我们可以说这个图关于连通性具有 2 的弹性。请注意,这并不意味着移除任何两条边都会破坏这个图的连通性。图 3 展示了在移除两条边后仍然保持图连通的可能性。
-
图 1
-
图 2
-
图 3
根据这个定义,给定图在不同属性方面将具有不同的弹性值。因此,该定义是具体的,但灵活的,可以有效地应用于现实世界的网络,其中属性从不同角度来看具有不同的重要性。
一些关于弹性的讨论侧重于顶点移除而不是边移除。移除一个顶点对网络其余部分的影响等同于移除连接到该顶点的所有边的影响。
上面的例子突出了随机边移除和目标边移除之间的区别。如果随机移除边,属性可能会在移除许多边后仍然存在。目标边移除意味着分析图并选择能够达到最小值的边。[3]
两种类型的边移除对网络的影响部分取决于度分布。遵循幂律分布(无标度)的图往往对随机边移除具有很强的弹性,因为移除的边很有可能只连接低度顶点,因此整体图结构只会受到轻微影响。然而,它们对连接到高度顶点的边的目标移除,特别是对这些顶点本身的移除,要脆弱得多。在无标度图中,这些高度顶点在连接子图方面至关重要。[3]
一个在某个属性方面弹性低的图,可能会因为仅仅移除几条边而失去该属性。我们可以说该图在该属性方面很脆弱。
但这仅仅是对脆弱性完整考虑的一部分。另一半则要考虑如果该属性丢失对网络性能的影响,这在运输地理与网络科学/可靠性中讨论。

在图论中,弹性是一个二元概念:一条边要么存在,要么不存在;一个图要么具有某个属性,要么不具有。在现实世界的交通网络中,链路具有额外的属性,例如容量和成本。我们可以通过考虑链路属性变化对整体网络属性的影响,将弹性的概念应用于交通网络。

例如,考虑图 4 中的网络,其中节点表示城市,链路表示货运铁路。每条链路都有一个成本,表示穿越它的所需时间(以小时为单位)。网络的一个属性是存在一条从 A 到 D 的路径,其总成本为 10 小时或更少。现在想象一下,发生了一些事件,导致 A-D 链路的成本增加了 50%,达到 15。事件的具体性质无关紧要;它可能是暴风雪、疲劳的铁轨或政府实施的限速。这个事件足以破坏网络具有从 A 到 D 的 10 小时或更少成本路径的属性。
然而,它并没有破坏网络的连通性属性;A 和 D 仍然是连通的(尽管路径成本更高)。在评估交通网络的弹性时,重要的是要记住,网络在不同属性方面将具有不同的弹性水平。
一旦评估了网络在某个属性方面的弹性,通常希望提高弹性。这可以通过两种基本方法来实现:添加冗余或过度配置现有链路。(Bell 2000,前言)
想象一下,我们可以将链路 A-B 和 C-D 的成本从 8 降低到 6,如图 5 所示。这个改进后的网络具有三条从 A 到 D 的节点独立路径,成本为 10 小时或更少。如果同一个事件发生在这个网络中,该属性就不会被破坏。破坏改进后的网络中相同属性所需的变化次数比原始网络多。因此,我们可以说改进后的网络在这个属性方面更具弹性。
如果一条链路的容量超过处理正常流量所需的容量,则称其为过度配置。这种“备用容量”可以帮助链路,从而帮助整个网络在链路容量下降时保持足够的性能水平。容量仍然会下降,但仍然能够提供所需的 服务水平。在我们的例子中,我们可以通过升级 A-D 链路使其初始成本为 6 来表示过度配置。同一个导致成本增加 50% 的事件现在将导致 9 小时的成本——仍然低于 10 小时的所需服务水平。
Murry-Tuite 提出,“韧性是一种特性,表明系统在非常规条件下的性能、恢复速度以及恢复到原始功能状态所需的外部援助量”[4] [5]。根据 Heaslip 等人的定义,“韧性是指系统在指定时间范围内保持其已展示的服务水平或恢复到该服务水平的能力”[6] [7]。
Heaslip 还引入了韧性循环的概念,它包含四个阶段:正常状态、故障、自我退火和恢复[8] [9]。韧性循环如图所示。

正常状态指的是网络在没有受到任何干扰的情况下运行,网络作为一个正常的运行系统发挥作用。在这个阶段,网络具有最大的效率[10] [11]。故障阶段始于干扰事件的发生。它描述了效率突然或逐渐下降的整个过程,取决于干扰事件的特性。在故障阶段结束时,效率下降到最低点[12] [13]。自我退火阶段紧随故障阶段,网络本身和网络用户都试图应对故障情况。紧急管理措施旨在缓解故障情况,网络用户可以选择替代路线或交通方式。网络的效率开始上升,但幅度很小[14] [15]。
恢复阶段是指故障阶段造成的干扰被修复,例如清除障碍物或恢复损坏的设施。恢复速度,定义为快速性,取决于恢复过程中使用的技术或资源。之后,系统可能进入一个新的正常状态。其效率可能与原始效率相同,也可能不同[16] [17]。
韧性循环的图形图示见图 9[18]。
该图显示了网络性能从旧正常状态到新正常状态的变化,这是由于故障阶段发生的干扰造成的。干扰可以根据故障阶段持续的时间分为逐步事件和突然事件。恢复线的斜率是我们之前提到的快速性。恢复后,系统可能出现三种情况:比旧正常状态好、与旧正常状态相同或比旧正常状态差。实线和虚线之间的区域表示由于干扰造成的总性能损失[19]。
考虑到可以采用不同的指标来评估网络性能,因此总性能损失对于这些指标可能会有不同的表现形式,例如连通性、容量、可达性等。例如,一个具有四个节点和五条连接的网络,其连通性如图 1、2 和 3 所示。
另一个关于容量的示例网络描述如下。该网络的图示见 [[1]] 中的图 4。假设在旧正常状态下,每条连接的容量是该图中连接旁边显示的值。在这个阶段,网络能够保持其性能,具有相对较高的容量来满足交通需求。假设在连接 AD 发生了干扰,例如交通事故或道路维修,导致其容量下降至 5。当一些驾驶员选择连接 AC 和连接 CD 从节点 A 到节点 D,而不是直接选择连接 AD,或者网络管理开始处理这种干扰时,网络可以被视为处于自我退火阶段。在事件解决后,网络可以自行恢复。此外,如果事件是为了维护道路状况,新的正常状态可能比旧正常状态具有更高的性能。
- ↑ Sudakov and Vu 2008,“图的局部韧性”。http://www.math.ucla.edu/~bsudakov/resilience.pdf
- ↑ Sudakov 2008
- ↑ a b Newman 2003
- ↑ Murray-Tuite,Pamela M. “在模拟系统最优和用户均衡条件下比较交通网络韧性。”仿真会议,2006 年。WSC 06。冬季会议论文集。IEEE,2006 年。
- ↑ Pant,Sunil Babu,“交通网络韧性:自我退火研究”(2012 年)。所有研究生论文和学位论文。论文编号 1434。
- ↑ Heaslip,Kevin 等人。“一种用于评估交通网络对自然灾害和人为事件韧性的草图级方法。”交通研究委员会第 89 届年会。编号 10-3185。2010 年。
- ↑ Pant,Sunil Babu,“交通网络韧性:自我退火研究”(2012 年)。所有研究生论文和学位论文。论文编号 1434。
- ↑ Heaslip,K.,Louisell,W.C.,Collura,J.,2009 年。区域网络交通韧性的定量评估,交通研究委员会第 88 届年会,华盛顿特区。
- ↑ Pant,Sunil Babu,“交通网络韧性:自我退火研究”(2012 年)。所有研究生论文和学位论文。论文编号 1434。
- ↑ Heaslip,K.,Louisell,W.C.,Collura,J.,2009 年。区域网络交通韧性的定量评估,交通研究委员会第 88 届年会,华盛顿特区。
- ↑ Pant,Sunil Babu,“交通网络韧性:自我退火研究”(2012 年)。所有研究生论文和学位论文。论文编号 1434。
- ↑ Heaslip,K.,Louisell,W.C.,Collura,J.,2009 年。区域网络交通韧性的定量评估,交通研究委员会第 88 届年会,华盛顿特区。
- ↑ Pant,Sunil Babu,“交通网络韧性:自我退火研究”(2012 年)。所有研究生论文和学位论文。论文编号 1434。
- ↑ Heaslip,K.,Louisell,W.C.,Collura,J.,2009 年。区域网络交通韧性的定量评估,交通研究委员会第 88 届年会,华盛顿特区。
- ↑ Pant,Sunil Babu,“交通网络韧性:自我退火研究”(2012 年)。所有研究生论文和学位论文。论文编号 1434。
- ↑ Heaslip,K.,Louisell,W.C.,Collura,J.,2009 年。区域网络交通韧性的定量评估,交通研究委员会第 88 届年会,华盛顿特区。
- ↑ Pant,Sunil Babu,“交通网络韧性:自我退火研究”(2012 年)。所有研究生论文和学位论文。论文编号 1434。
- ↑ Pant,Sunil Babu,“交通网络韧性:自我退火研究”(2012 年)。所有研究生论文和学位论文。论文编号 1434。
- ↑ Pant,Sunil Babu,“交通网络韧性:自我退火研究”(2012 年)。所有研究生论文和学位论文。论文编号 1434。