三角学/正弦波形

三角多项式

我们首先考虑 **三角多项式**。 这些函数是不同正弦和余弦函数的总和。 例如

$f(x)=5+3\cos(x)+2\sin(2x)-5\cos(4x)$

是一个三角多项式。 一般来说，三角多项式具有以下形式

$A_{0}+\sum _{n=1}^{N}{\bigl [}A_{n}\cos(nx)+B_{n}\sin(nx){\bigr ]}$

实际上，这里潜在的想法与普通多项式没什么不同。 我们正在形成对我们熟知的函数的线性组合。 使用普通多项式，函数是 $x^{n}$，其中 $n=0,1,2,3,\dots$。 这里的函数是 $\cos(nx)$ 或 $\sin(nx)$，其中 $n=0,1,2,3,\dots$

实例 我们可以而且将会定义三角多项式的次数，并讨论它们的各种性质，但在我们深入研究之前，注意到哪些函数可以写成三角多项式可能很有趣。 例如，考虑 $f(x)=\cos(3x)\sin(5x)$ 乍一看它不像三角多项式，但如果我们使用角和公式来计算 ${\frac {\sin(5x+3x)-\sin(5x-3x)}{2}}$，我们会发现它是 $f(x)=\cos(3x)\sin(5x)={\frac {\sin(8x)-\sin(2x)}{2}}$

练习：另一种方法？ $\sum _{n=0}^{N}{\bigl [}A_{n}\cos(nx)+B_{n}\sin(nx){\bigr ]}$ 看看上面三角多项式的公式。 它是否包含相同的函数？

练习：三角多项式 表达 $\sin ^{2}(x)$ 作为关于 $x$ 的三角多项式

练习：组合三角多项式 如果 $g(x)$ 是一个普通的代数多项式，那么 $g(x)^{2}$ 也是一个代数多项式， $g{\bigl (}g(x){\bigr )}$ 也是。这种说法对三角多项式是否也适用呢？

除了角的和公式，我们还有另一个非常有用的工具。在许多令人惊叹的三角函数属性中，$\sin(x)$ 和 $cos(x)$ 是所谓的正交性关系。这些是关于积分的以下结果：

$\int \limits _{-\pi }^{\pi }\sin(nx)\sin(mx)dx={\begin{cases}0&{\text{if }}n\neq m\\2\pi &{\text{if }}n=m\end{cases}}$

类似地，

$\int \limits _{-\pi }^{\pi }\cos(nx)\cos(mx)dx={\begin{cases}0&{\text{if }}n\neq m\\2\pi &{\text{if }}n=m\end{cases}}$

$\int \limits _{-\pi }^{\pi }\cos(nx)\sin(mx)dx=0\quad {\text{for all }}n{\text{ and }}m.$

待办事项：使用对称性绘制图形来展示非正式论证，以说明为什么这样。

例如，以我们开始时用到的函数为例， $f(x)=5+3\cos(x)+2\sin(2x)-5\cos(4x)$，我们可以计算

${\begin{aligned}&{\frac {1}{\pi }}\int \limits _{-\pi }^{\pi }f(x)\cos(x)dx\\&={\frac {5}{\pi }}\int \limits _{-\pi }^{\pi }\cos(x)dx+{\frac {3}{\pi }}\int \limits _{-\pi }^{\pi }\cos ^{2}(x)dx+{\frac {2}{\pi }}\int \limits _{-\pi }^{\pi }\sin(x)\cos(x)dx-{\frac {5}{\pi }}\int \limits _{-\pi }^{\pi }\cos(x)\cos(4x)dx\\&=0+{\frac {3}{\pi }}\cdot \pi +0+0=3\end{aligned}}$

注意最后一行遵循我们上面计算的积分。这意味着我们可以使用积分来确定三角多项式的系数。这是一个有趣的想法，因为并非所有三角多项式乍一看都是三角多项式。问题变成了我们如何知道什么时候停止计算三角多项式的系数？我们如何知道我们是否找到了所有系数？一个答案可能是比较图形。我们首先证明，当我们知道要走多远时，这个想法可以用在这种情况中，例如让

$f(x)=5+3\cos(x)+2\sin(2x)-\sin(3x)-{\tfrac {1}{8}}\cos(4x)$

然后数值计算 $A_{n}$ 和 $B_{m}$ 的积分。我们可以从图中看到我们何时计算了所有系数，如下面的动画所示。

让我们尝试另一个我们不知道三角多项式阶数的例子。函数 $f(x)=5\sin(x)\cos ^{2}(2x)+\sin ^{14}(12x)$ 可以写成三角多项式，我们积分求系数并通过查看图形来判断何时完成的过程可以使用，下面是动画演示。

注意，对于这个特定函数，要决定何时结束需要相当长的时间。事实证明，我们必须一直到 **N=48** 才能找到所有系数。这看起来可能是个问题，特别是如果我们不小心从一个不是三角多项式的函数开始。

为了看看会发生什么，让我们假设我们从一个方波开始，也就是说，我们让

$f(x)={\begin{cases}1&{\text{if }}0\leq x\leq \pi \\-1&{\text{if }}-\pi <x<1\end{cases}}$

并且 $f(x)$ 被定义为周期为 $2\pi$ 的周期函数，即我们定义 $f(x+2\pi )=f(x)$。如果我们在 $f(x)$ 上使用我们的过程，那么我们很快就会发现它似乎永远不会停止，如动画所示

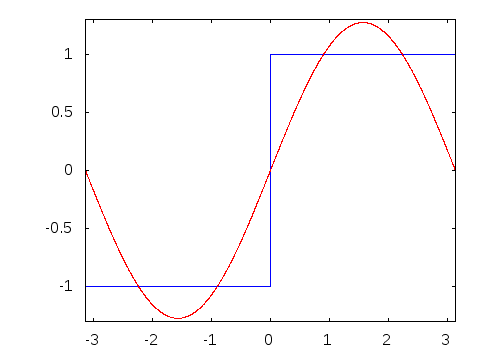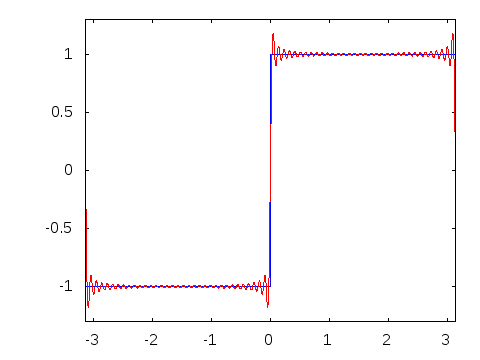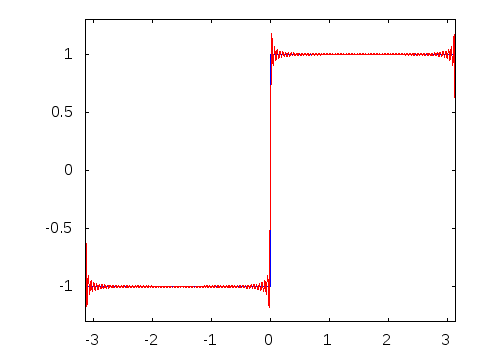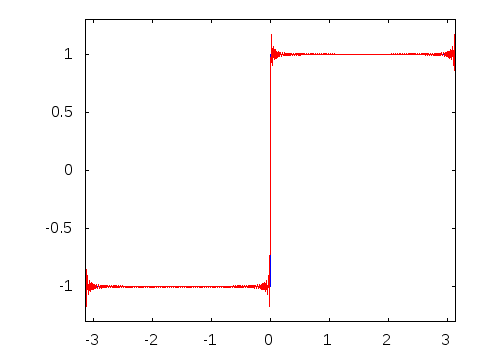
此动画显示，当我们在三角多项式中增加项数时，我们永远无法完全达到原始函数。另一方面，我们越来越接近，尤其是在远离$x=-\pi ,0,\pi$ 的地方。

有了这样的动机，我们可以提出一个大胆的问题：如果我们让项数趋于无穷，三角多项式是否会收敛到方波？这就是傅里叶级数研究的起点。